 Este texto consolidado es de carácter informativo y no tiene valor jurídico.
Este texto consolidado es de carácter informativo y no tiene valor jurídico.El Real Decreto 1434/2010, de 5 de noviembre, sobre interoperabilidad del sistema ferroviario de la Red Ferroviaria de interés general, incorpora al derecho interno la Directiva 2008/57/CE del Parlamento Europeo y del Consejo, de 17 de junio de 2008, sobre la interoperabilidad del sistema ferroviario dentro de la Comunidad. Dicha Directiva 2008/57/CE establece las condiciones que deben cumplirse para lograr en el territorio comunitario la interoperabilidad del sistema ferroviario.
La necesidad de definir los gálibos a considerar, tanto para la construcción de vehículos, la colocación de elementos próximos a la vía, así como el cargamento en vagones abiertos es fundamental a fin de garantizar la seguridad de la circulación ferroviaria, al evitarse las interferencias entre los vehículos, y de éstos con la infraestructura y se materializa dicha necesidad en la Instrucción que se aprueba por la presente orden.
La Instrucción que figura en el anexo se ha redactado en coherencia con la norma de gálibos EN 15273:2013 y respeta las especificaciones técnicas de interoperabilidad de los subsistemas de infraestructura, material rodante y energía de los sistemas ferroviarios transeuropeos convencional y de alta velocidad.
Esta Orden ha sido sometida a los trámites establecidos en el Real Decreto 1337/1999, de 31 de julio, por el que se regula la remisión de información en materia de normas y reglamentaciones técnicas y reglamentos relativos a los servicios de la sociedad de la información, que incorpora al ordenamiento jurídico español la Directiva 98/34/CE, del Parlamento Europeo y del Consejo, de 22 de junio, modificada por la Directiva 98/48/CE, del Parlamento Europeo y del Consejo, de 20 de julio, por la que se establece un procedimiento de información en materia de las normas y reglamentaciones técnicas.
La Orden se ha tramitado de conformidad con lo dispuesto en el artículo 15 del Reglamento del Sector Ferroviario, aprobado por el Real Decreto 2387/2004, de 30 de diciembre, que autoriza al Ministro de Fomento a aprobar las normas e instrucciones que rijan los proyectos básicos o de construcción de las infraestructuras ferroviarias y aquellas a las cuales deban sujetarse los trabajos y obras de construcción de las mismas.
En su virtud, a iniciativa de la Agencia Estatal de Seguridad Ferroviaria, a propuesta del Secretario General de Infraestructuras y con la conformidad del Secretario de Estado de Infraestructuras, Transporte y Vivienda, dispongo:
Se aprueba mediante esta orden la Instrucción de gálibos ferroviarios que se inserta a continuación.
Lo dispuesto en esta Orden no será de aplicación a:
1. Los proyectos de nueva construcción de infraestructuras ferroviarias o de acondicionamiento de las existentes, cuya correspondiente orden de estudio se hubiese dictado con anterioridad a la entrada en vigor de la presente orden.
2. Las obras que se realicen en desarrollo de los proyectos a los que se refiere el punto anterior.
Se faculta a la Agencia Estatal de Seguridad Ferroviaria para dictar las instrucciones que sean necesarias para la aplicación e interpretación de esta Orden.
La presente Orden entrará en vigor el día siguiente al de su publicación en el «Boletín Oficial del Estado».
Madrid, 14 de julio de 2015.–La Ministra de Fomento, Ana María Pastor Julián.
ÍNDICE
1. INTRODUCCIÓN
1.1 Objeto
1.2 Ámbito de aplicación
1.2.1 Gálibo del material rodante.
1.2.2 Gálibo de implantación de obstáculos.
1.3 Gálibos considerados
1.3.1 Gálibo del material rodante.
1.3.2 Gálibo de implantación de obstáculos.
1.3.3 Compatibilidad entre el material rodante y la infraestructura.
1.4 Convenio entre el material rodante y la infraestructura
1.5 Notación y unidades
2. GÁLIBO DE MATERIAL RODANTE
2.1 Consideraciones generales
2.2 Reglas asociadas
2.2.1 Reducciones y ampliaciones a considerar.
2.2.2 Desplazamientos verticales.
2.2.3 Desplazamientos horizontales.
2.3 Cálculo del gálibo del material rodante
2.4 Cálculo del gálibo de vehículos de caja inclinable VCI
2.4.1 Sistemas de inclinación de las cajas.
2.4.2 Condiciones de partida.
2.4.3 Reglas asociadas.
2.4.4 Condiciones sobre la velocidad de los VCI.
2.5 Cálculo del gálibo del pantógrafo en posición de captación
2.5.1 Pantógrafos en vehículos clásicos.
2.5.2 Pantógrafos en vehículos de caja inclinable.
2.5.3 Contorno de referencia de los pantógrafos y de las partes del vehículo susceptibles de estar en tensión eléctrica, no aisladas, situadas en el techo
2.6 Elementos retráctiles en posición de apertura
2.7 Aplicación a líneas con ancho ibérico
2.7.1 Contornos de referencia.
2.7.2 Reglas asociadas.
2.7.3 Cálculo del gálibo del material.
2.7.4 Cálculo del gálibo de vehículos de caja inclinable.
2.7.5 Cálculo del gálibo del pantógrafo en posición de captación.
2.7.6 Situación de peldaños.
2.8 Aplicación a líneas con ancho estándar europeo
2.8.1 Contornos de referencia.
2.8.2 Reglas asociadas.
2.8.3 Cálculo del gálibo del material.
2.8.4 Cálculo del gálibo de vehículos de caja inclinable.
2.8.5 Cálculo del gálibo del pantógrafo en posición de captación.
2.8.6 Situación de peldaños.
2.9 Aplicación a líneas con ancho métrico
2.9.1 Contornos de referencia.
2.9.2 Reglas asociadas.
2.9.3 Cálculo del gálibo del material.
2.9.4 Cálculo del gálibo del pantógrafo en posición de captación.
3. GÁLIBO DE LAS INSTALACIONES FIJAS
3.1 Gálibos de implantación de obstáculos
3.2 Reglas asociadas
3.2.1 Ampliaciones a considerar.
3.2.2 Desplazamientos laterales.
3.2.3 Desplazamientos perpendiculares al plano de rodadura.
3.3 Gálibo límite de implantación de obstáculos
3.4 Gálibo nominal de implantación de obstáculos
3.5 Gálibo del pantógrafo
3.5.1 Determinación del gálibo mecánico del pantógrafo.
3.5.2 Determinación del gálibo eléctrico del pantógrafo.
3.6. Distancia entre ejes de vías (entreeje)
3.6.1 Parámetros que intervienen.
3.6.2 Determinación del entreeje límite.
3.6.3 Determinación del entreeje nominal.
3.7 Gálibo en elementos específicos
3.7.1 Elementos de trazado con variación de curvatura en planta.
3.7.2 Andenes.
3.7.3 Aceras de evacuación en túneles.
3.7.4 Paseos de servicio para mantenimiento.
3.7.5 Muelles.
3.7.6 Apeos de vía.
3.7.7 Gálibo en zona de obras autorizadas por el administrador de infraestructura
3.8 Transiciones de los frenos de vía en posición activa
3.9 Vehículos de caja inclinable
3.10 Aplicación a líneas con ancho ibérico
3.10.1 Reglas asociadas
3.10.2 Gálibo límite de implantación de obstáculos.
3.10.3 Gálibo nominal de implantación de obstáculos.
3.10.4 Gálibo del pantógrafo.
3.10.5 Distancia entre ejes de vías.
3.10.6 Distancia entre eje de vía y borde de andén.
3.10.7 Gálibo uniforme de implantación de obstáculos.
3.10.8 Características de los vehículos de referencia.
3.11 Aplicación a líneas con ancho estándar europeo
3.11.1 Reglas asociadas
3.11.2 Gálibo límite de implantación de obstáculos.
3.11.3 Gálibo nominal de implantación de obstáculos.
3.11.4 Gálibo del pantógrafo.
3.11.5 Distancia entre ejes de vías.
3.11.6 Distancia entre eje de vía y borde de andén.
3.11.7 Gálibo uniforme de implantación de obstáculos.
3.11.8 Características de los vehículos de referencia.
3.12 Aplicación a líneas con ancho métrico
3.12.1 Reglas asociadas
3.12.2 Gálibo límite de implantación de obstáculos.
3.12.3 Gálibo nominal de implantación de obstáculos.
3.12.4 Gálibo del pantógrafo.
3.12.5 Distancia entre ejes de vías.
3.12.6 Distancia entre eje de vía y borde de andén.
3.12.7 Gálibo uniforme de implantación de obstáculos.
3.12.8 Características de los vehículos de referencia.
4. GÁLIBO DE CARGAMENTO
4.1 Consideraciones generales
4.2 Reglas asociadas
4.2.1 Reducciones y ampliaciones a considerar.
4.2.2 Desplazamientos horizontales.
4.3 Cálculo del gálibo del cargamento
4.4 Aplicación a líneas con ancho ibérico
4.4.1 Contornos de referencia.
4.4.2 Reglas asociadas.
4.4.3 Cálculo del gálibo de cargamento.
4.5 Aplicación a líneas con ancho estándar europeo
4.5.1 Contornos de referencia.
4.5.2 Reglas asociadas.
4.5.3 Cálculo del gálibo de cargamento.
4.6 Aplicación a líneas con ancho métrico
4.6.1 Contornos de referencia.
4.6.2 Reglas asociadas.
4.6.3 Cálculo del gálibo de cargamento.
4.7 Cuadros de reducción
4.7.1 Cuadros de reducción de la anchura del cargamento en secciones internas y externas.
4.7.2 Cuadros de reducción de la anchura del cargamento respecto las paredes laterales o teleros en vagones de seguridad e intermedios.
ANEJO 1. DEFINICIONES
ANEJO 2. LISTADO DE PARÁMETROS
ANEJO 3. GÁLIBOS HISTÓRICOS
A.3.1 Tipos.
A.3.2 Contornos de referencia del gálibo cinemático.
A.3.3 Gálibo del material rodante.
A.3.4 Gálibo de implantación de obstáculos.
ANEJO 4. JUSTIFICACIÓN DE LOS NUEVOS CONTORNOS DE REFERENCIA DE LOS GÁLIBOS CINEMÁTICOS Y ESTÁTICOS
A.4.1 Definición de nuevos gálibos.
A.4.2 Contornos de referencia de los gálibos cinemáticos.
A.4.3 Contornos de referencia de los gálibos estáticos.
ANEJO 5. EJEMPLOS DE CÁLCULO DEL GÁLIBO DEL MATERIAL RODANTE
A.5.1 Cálculo de una locomotora.
A.5.2 Cálculo de un vagón cisterna.
A.5.3 Cálculo de un vehículo autopropulsado.
ANEJO 6. EJEMPLOS DE CÁLCULO DEL GÁLIBO DEL MATERIAL RODANTE EN VEHÍCULOS DE CAJA INCLINABLE
A.6.1 Cálculo de un VCI con sistema activo.
A.6.2 Cálculo de un VCI con sistema pasivo.
ANEJO 7. EJEMPLOS DE CÁLCULO DE GÁLIBOS LÍMITE Y UNIFORME DE IMPLANTACIÓN DE OBSTÁCULOS, ENTREEJE LÍMITE Y GÁLIBO DEL PANTÓGRAFO
A.7.1 Gálibo límite de implantación de obstáculos.
A.7.2 Gálibo mecánico y eléctrico del pantógrafo.
A.7.3 Gálibo uniforme de implantación de obstáculos.
A.7.4 Entreeje límite.
ANEJO 8. CUADROS DE SEMIANCHOS DE LOS GÁLIBO DE CARGAMENTO
A.8.1 Gálibo GHE16.
A.8.2 Gálibo GEA16.
A.8.3 Gálibo GEB16.
A.8.4 Gálibo GEC16.
A.8.5 Gálibo GA.
A.8.6 Gálibo GB.
A.8.7 Gálibo GC.
A.8.8 Gálibo GEE10.
A.8.9 Gálibo GED10.
ANEJO 9. CUADROS DE REDUCCIÓN DE LA ANCHURA DEL CARGAMENTO EN SECCIONES INTERNAS
A.9.1 Gálibos GHE16, GEA16, GEB16, GEC16, GA, GB Y GC.
A.9.2 Gálibos GEE10 y GED10.
ANEJO 10. CUADROS DE REDUCCIÓN DE LA ANCHURA DEL CARGAMENTO EN SECCIONES EXTERNAS
A.10.1 Gálibos GHE16, GEA16, GEB16, GEC16, GA, GB Y GC.
A.10.2 Gálibos GEE10 y GED10.
A.10.3 Ejemplo de cálculo de la reducción de la anchura del cargamento mediante cuadros.
ANEJO 11. EJEMPLOS DE APLICACIÓN DE LAS FÓRMULAS DEL GÁLIBO DEL CARGAMENTO
A.11.1 Gálibo GEB16.
A.11.2 Gálibo GEC16.
ANEJO 12. DISTANCIA MÍNIMA ENTRE EL CARGAMENTO Y LAS PAREDES LATERALES O TELEROS EN VAGONES DE SEGURIDAD E INTERMEDIOS
A.12.1 Gálibos GHE16, GEA16, GEB16, GEC16, GA, GB Y GC.
1.1 OBJETO
Esta Instrucción tiene por objeto definir los gálibos a considerar, tanto para la construcción de vehículos (gálibo del material rodante), como para la colocación de elementos próximos a la vía (gálibo de implantación de obstáculos).
Asimismo se definen los gálibos de cargamento en vagones abiertos, así como las distancias mínimas que el cargamento debe mantener con las paredes laterales o teleros de los vagones de carga.
El cumplimiento de esta Instrucción garantiza la seguridad de la circulación ferroviaria, al evitarse las interferencias entre los vehículos, y de éstos con la infraestructura.
Esta Instrucción se ha redactado en coherencia con la norma de gálibos EN 15273:2013 y respeta las especificaciones técnicas de interoperabilidad de los subsistemas de infraestructura, material rodante y energía de los sistemas ferroviarios transeuropeos de alta velocidad y convencional.
1.2 ÁMBITO DE APLICACIÓN
1.2.1 GÁLIBO DEL MATERIAL RODANTE
Esta Instrucción es de aplicación a la definición del gálibo del material rodante, a considerar en el proyecto de los perfiles constructivos de cualquier tipo de material motor o remolcado, ya sea nuevo ó acondicionado.
A los efectos de esta Instrucción, se considera «material acondicionado» aquél cuyas modificaciones afectan a su perfil constructivo.
El material motor o remolcado, proyectado, construido o acondicionado antes de la entrada en vigor de la presente Instrucción podrá circular en las condiciones actuales de inscripción en gálibo, sin ninguna limitación derivada de la aprobación de la misma.
Las fórmulas para la obtención de los gálibos del material rodante y del cargamento definidos en esta Instrucción son de aplicación directa a vehículos de caja suspendida sobre dos ejes o sobre dos bogies de dos ejes cada uno, así como a vehículos articulados simétricos. Para el resto, deberán adaptarse las fórmulas a la configuración geométrica real de sus elementos de rodadura.
La figura 1.1 muestra la equivalencia entre las unidades articuladas simétricas y los vehículos de dos ejes o de dos bogies.
|
Figura 1.1. Equivalencia entre unidades articuladas simétricas y vehículos aislados |
1.2.2 GÁLIBO DE IMPLANTACIÓN DE OBSTÁCULOS
Esta Instrucción es de aplicación a la definición del gálibo de implantación de obstáculos a considerar en el proyecto de líneas ferroviarias de nueva construcción ó de acondicionamiento de las existentes, integradas en la red ferroviaria de interés general de anchos ibérico, estándar europeo, o métrico (excepto la línea Cercedilla-Cotos).
A los efectos de esta Instrucción, se considera como «acondicionamiento de una línea existente», cualquier actuación de mejora de ésta que incremente alguno de sus parámetros característicos (gálibo, carga por eje admisible, velocidad o longitud máxima permitida de tren) o bien su capacidad.
Las obras de acondicionamiento que requieren una nueva autorización de puesta en servicio deberán cumplir los gálibos definidos en el apartado 1.3.2. Son las siguientes:
– Modificación sustancial del trazado en parte de un itinerario existente.
– Adición de una o más vías en un itinerario existente, cuando la separación entre la existente y la nueva sea significativa.
– En general, aquellas que hayan requerido la redacción de un estudio informativo para su tramitación administrativa.
Las obras de modificación del ancho de vía o de adición de uno o más carriles a la vía existente, serán asimilables a un acondicionamiento, por lo que deberán cumplir la presente Instrucción.
En las obras de acondicionamiento de líneas existentes que no requieran una nueva autorización de puesta en servicio, se recomienda el cumplimiento de la presente Instrucción. En caso contrario, el promotor informará a la Autoridad ferroviaria de las razones para ello.
Las actuaciones en líneas existentes que supongan la implantación o cambio de ubicación de elementos aledaños a la vía (por ejemplo: estructuras, instalaciones de electrificación o de seguridad y comunicaciones), se realizarán respetando el gálibo de implantación de obstáculos definido en el cuadro 1.2 para líneas acondicionadas.
La definición de los gálibos históricos se incluye en el anejo 3.
Las líneas ferroviarias existentes no acondicionadas se podrán catalogar como de gálibos GEA16, GEB16 ó GEC16, cuando tras un estudio detallado se compruebe que respetan el gálibo límite de implantación de obstáculos.
1.3 GÁLIBOS CONSIDERADOS
En la figura 1.2 se definen los diferentes tipos de gálibos y contornos considerados en esta Instrucción.
|
(1) Gálibo de implantación de obstáculos (2) Perfil constructivo máximo del material (3) Suma de los movimientos del vehículo y de los fenómenos de interacción con la infraestructura (4) Infraestructura (5) Vehículo (6) Contorno de referencia Figura 1.2. Gálibos considerados |
Para cada gálibo (GHE16, GEA16, GA, etc.) se define un contorno de referencia. A partir de éste, y mediante la aplicación de unas reglas asociadas, se obtienen el gálibo del material rodante y el gálibo de implantación de obstáculos correspondientes a ese gálibo.
En el cuadro 1.1 se definen los diferentes contornos de referencia considerados en esta Instrucción para los distintos anchos de vía nominal.
El contorno de referencia del gálibo G1, se define en la norma EN 15273-3:2013.
| TIPOS DE GÁLIBO | ANCHO DE VÍA (mm) | ||
|---|---|---|---|
| 1668 | 1435 | 1000 | |
| NUEVOS | GEA16 | GA | GED10 |
| GEB16 | GB | GEE10 | |
| GEC16 | GC | ||
| HISTÓRICOS | GHE16 | GEC14 | |
| GC14 | |||
|
Cuadro 1.1. Contornos de referencia |
|||
Además, en cada punto kilométrico de la línea, y para cada gálibo (GHE16, GEA16, GA, etc.), se definen unos gálibos límite y nominal de implantación de obstáculos, que son función de las características del trazado (radio, peralte, etc.) en ese punto. Comparativamente, el gálibo nominal es algo mayor que el límite, al incorporar márgenes para futuros incrementos de velocidad, paso de transportes excepcionales, etc.
Para evitar tener un gálibo distinto en cada punto de la línea, se define un gálibo uniforme, que es envolvente de los gálibos nominales, y que se obtiene para unas características de trazado suficientemente desfavorables, como para no ser superadas más que excepcionalmente en algún punto de la línea.
Los gálibos se denominan mediante unas siglas cuyo significado es el siguiente:
a) Para los gálibos en líneas con ancho de vía estándar europeo o ibérico:
– G: Gálibo
– H: Histórico
– E: Español
– A: Gálibo envolvente del gálibo GA
– B: Gálibo envolvente del gálibo GB
– C: Gálibo envolvente del gálibo GC
– Las dos cifras indican el ancho de vía redondeado a decímetros
Para los gálibos G1, GA, GB y GC por tratarse de gálibos interoperables europeos se omite la indicación del ancho de vía, al entenderse que solo se definen para el ancho estándar europeo.
b) Para los gálibos en líneas con ancho de vía métrico:
– G: Gálibo
– E: Español
– E: Eléctrico
– D: Diesel
– Las dos cifras indican el ancho redondeado a decímetros
1.3.1 GÁLIBO DEL MATERIAL RODANTE
El registro de infraestructura especificará los gálibos admitidos en cada línea o sección de línea. No obstante, el Administrador de la Infraestructura podrá autorizar la circulación por la línea, de material rodante con gálibos mayores.
El diseño del material rodante interoperable (que cumple con los gálibos G1, GA, GB o GC) se realizará de acuerdo con las Especificaciones Técnicas de Interoperabilidad del material rodante correspondientes.
1.3.2 GÁLIBO DE IMPLANTACIÓN DE OBSTÁCULOS
En general, el gálibo de implantación de obstáculos a respetar en líneas nuevas o acondicionadas será el gálibo uniforme de implantación de obstáculos.
En situaciones excepcionales, como consecuencia de condicionantes técnicos o económicos, la Autoridad Ferroviaria podrá autorizar en determinados tramos o secciones de la línea un gálibo límite o nominal de implantación de obstáculos obtenido a partir de los parámetros de trazado de ese tramo o sección.
En las actuaciones que afecten a la electrificación de líneas existentes, y siempre que sea compatible con las exigencias de explotación, se valorará la posible instalación de catenaria rígida, si ésta facilita la futura implantación de los gálibos definidos en el cuadro 1.2.
Mediante Resolución, la Autoridad Ferroviaria podrá establecer en determinados corredores, gálibos superiores a los definidos en el cuadro 1.2, a fin de permitir ciertos tipos de tráfico.
Las líneas existentes en las que se varíe el ancho de vía nominal de 1668 mm a 1435 mm con descentramiento del eje de la vía, deberán respetar como mínimo el gálibo límite de implantación de obstáculos calculado a partir de las características de la línea.
En el caso de vía con tres hilos, para la circulación simultánea de vehículos en ancho ibérico y estándar europeo, el gálibo de implantación de obstáculos será el envolvente de ambos.
En la memoria de todo proyecto de construcción de una línea nueva, o de acondicionamiento de una línea existente, se indicará el gálibo de implantación de obstáculos considerado.
Cuando en un tramo o línea solamente exista un pequeño número de secciones en las que no se pueda alcanzar el gálibo límite de implantación de obstáculos GEB16, se elaborará, a la mayor brevedad posible, un plan de modificación de dichas secciones.
La definición de los diferentes tipos de gálibos figura en el anejo 1.
Los gálibos de implantación de obstáculos a respetar serán los siguientes:
a) En líneas con ancho de vía estándar europeo o ibérico:
En el cuadro 1.2 se indican los gálibos de implantación de obstáculos a respetar en las partes altas en cada tipo de línea.
| Tipo de línea | Galibo uniforme de implantación de obstáculos | Gálibo en situaciones excepcionales | ||||
|---|---|---|---|---|---|---|
| Ancho de vía | 1435 mm | 1668 mm | Ancho mixto (tres carriles) (8) | 1435 mm | 1668 mm | Ancho mixto (tres carriles) |
| Líneas nuevas | GC | GEC16 | GEC16+GC |
(4) (5) |
(8) | |
| Líneas acondicionadas |
GC GB(1) |
GEC16 GEB16(2) |
GEC16+GC GEC16+GB(3) GEB16+GC(3) GEB16+GB(3) |
(6) | (7) | |
|
Cuadro 1.2. Gálibos de implantación de obstáculos en partes altas a considerar en cada tipo de línea (ancho de vía 1435 mm y 1668 mm) |
||||||
(1) Cuando mediante un estudio de viabilidad técnica y económica se demuestre la no conveniencia del gálibo GC.
(2) Cuando mediante un estudio de viabilidad técnica y económica se demuestre la no conveniencia del gálibo GEC16.
(3) Cuando mediante un estudio de viabilidad técnica y económica se demuestre la no conveniencia del gálibo GEC16+GC.
(4) Cuando para algún tramo de línea exista un itinerario alternativo que cumpla el gálibo uniforme de implantación de obstáculos, la Autoridad Ferroviaria podrá autorizar excepcionalmente en dicho tramo, por condicionantes técnicos o económicos, un gálibo mayor o igual al gálibo límite de implantación de obstáculos, calculado con las características del tramo.
(5) Cuando para algún tramo de línea no exista itinerario alternativo que cumpla el gálibo uniforme de implantación de obstáculos, la Autoridad Ferroviaria podrá autorizar excepcionalmente en dicho tramo, por condicionantes técnicos o económicos, un gálibo mayor o igual al gálibo nominal de implantación de obstáculos, calculado con las características del tramo.
(6) La Autoridad Ferroviaria podrá autorizar excepcionalmente por condicionantes técnicos o económicos, algún tramo con un gálibo mayor o igual al gálibo límite de implantación de obstáculos GB, calculado con las características del tramo.
(7) La Autoridad Ferroviaria podrá autorizar excepcionalmente, por condicionantes técnicos o económicos, algún tramo con el gálibo existente GHE16.
(8) Gálibo envolvente definido por la combinación del gálibo considerado en cada ancho, teniendo en cuenta la posición del tercer carril.
En el cuadro 1.3 se indican los gálibos de implantación de obstáculos a respetar en las partes bajas en cada tipo de línea.
En general se considerará en las partes bajas el gálibo uniforme de implantación de obstáculos, si bien con carácter excepcional, en el caso de líneas nuevas serán de aplicación las notas 4 y 5 indicadas en el cuadro 1.2.
En el caso de líneas acondicionadas la Autoridad Ferroviaria podrá autorizar excepcionalmente por condicionantes técnicos o económicos, algún tramo con un gálibo de partes bajas mayor o igual al gálibo límite de implantación de obstáculos, calculado con las características del tramo.
| Tipo de línea | Ancho de vía | |
|---|---|---|
| 1435 mm | 1668 mm | |
| Apta para transporte mediante autopista ferroviaria (1) | GI3 | GEI3 |
| No apta para transporte mediante autopista ferroviaria | GI2 | GEI2 |
|
Cuadro 1.3. Gálibos de implantación de obstáculos en partes bajas a considerar en cada tipo de línea (ancho de vía 1435 mm y 1668 mm) |
||
(1) El gálibo de partes bajas apto para transporte mediante autopista ferroviaria se establecerá en los nuevos corredores de mercancías y tráfico mixto así como en aquellos acondicionamientos de corredores existentes que determine la Autoridad Ferroviaria. En el caso de líneas acondicionadas la implementación de dicho gálibo deberá ir precedida de un estudio de viabilidad técnica y económica.
Las vías de las estaciones de clasificación se diseñarán para un gálibo GI2 en las líneas con ancho de vía nominal 1435 mm y GEI2 en las líneas con ancho de vía nominal 1668 mm, salvo donde existan frenos de vía, donde se adoptará el gálibo GI1 en las líneas con ancho de vía nominal 1435 mm y GEI1 en las líneas con ancho de vía nominal 1668 mm
En las líneas de ancho mixto el gálibo de partes bajas será una envolvente del gálibo considerado en cada ancho.
b) En líneas con ancho de vía métrico:
En los proyectos de líneas nuevas el gálibo uniforme de implantación de obstáculos será el GEE10, si bien en situaciones excepcionales serán aplicables las notas 4 y 5 del cuadro 1.2.
En los proyectos de líneas acondicionadas, el gálibo uniforme de implantación de obstáculos será el GEE10, no obstante la Autoridad Ferroviaria podrá autorizar por condicionantes técnicos o económicos el gálibo de implantación de obstáculos GED10, calculado con las características del tramo, o incluso mantener el gálibo existente.
1.3.3 COMPATIBILIDAD ENTRE EL MATERIAL RODANTE Y LA INFRAESTRUCTURA
El gálibo del material rodante deberá ser compatible con el gálibo de implantación de obstáculos de la línea por la que circule.
En el cuadro 1.4 se indican los gálibos de material rodante interoperable (G1, GA, GB y GC) compatibles con el gálibo de implantación de obstáculos en partes altas, independientemente del ancho de vía.
No se contemplan los gálibos de implantación de obstáculos G1, GA y GEA16 al estar englobados los dos primeros en el gálibo GB y el último en el GEB16.
| Gálibo de implantación de obstáculos | Gálibos de material rodante interoperable compatibles | |||
|---|---|---|---|---|
| G1 | GA | GB | GC | |
| GEB16 | X | X | X | |
| GEC16 | X | X | X | X |
| GB | X | X | X | |
| GC | X | X | X | X |
| GHE16 | X | |||
| GEC14 | X | X | X | X |
|
Cuadro 1.4. Compatibilidad entre material rodante interoperable e infraestructura (partes altas) |
||||
En el cuadro 1.5 se indican los gálibos de las partes bajas del material rodante interoperable (GI1, GI2 y GI3) compatibles con el gálibo de partes bajas de implantación de obstáculos, independientemente del ancho de vía.
| Gálibo de implantación de obstáculos | Gálibos de material rodante interoperable compatibles | ||
|---|---|---|---|
| GI1 | GI2 | GI3 | |
| GEI1 | X | ||
| GEI2 | X | ||
| GEI3 | X | X | |
|
Cuadro 1.5. Compatibilidad entre material rodante interoperable e infraestructura (partes bajas) |
|||
1.4 CONVENIO ENTRE EL MATERIAL RODANTE Y LA INFRAESTRUCTURA
Para la determinación del gálibo en un punto o tramo de la línea, se adopta el siguiente convenio entre el material rodante y la infraestructura:
‒ Se parte de un contorno de referencia cinemático a partir del cual se determinan los diferentes gálibos mediante la aplicación de las reglas asociadas del gálibo cinemático. Dicho contorno se define para vía en recta, ancho de vía nominal y sin peralte.
‒ Las reglas asociadas definen las reducciones a aplicar en cualquier sección del vehículo o de la infraestructura, respecto a dos ejes de coordenadas ortogonales contenidos en un plano perpendicular al eje de la vía, y que son los siguientes:
‒ Eje vertical Y, perpendicular al plano de rodadura en el eje de vía. Los desplazamientos y reducciones en altura se medirán paralelamente a este eje y por encima del eje X.
‒ Eje horizontal X, es la intersección de un plano perpendicular al eje de la vía con el plano de rodadura. Los desplazamientos y reducciones laterales se medirán paralelamente a este eje y a cada lado del eje Y.
Conviene puntualizar que, salvo en recta, el eje X no es realmente horizontal, ni el Y es vertical, sino que son paralelo y perpendicular, respectivamente, al plano de rodadura. No obstante se ha utilizado está denominación al resultar más intuitiva.
Para la aplicación de las reglas asociadas, se adoptan los parámetros del cuadro 1.6.
| Parámetro | Gálibo material rodante | Gálibo de obstáculos |
|---|---|---|
| D ó I | Do ó I o | (D-Do) ó (I-I o) |
| s | s | s o |
| h c | h c | h co |
| η o | (η o -1) >0 | 1.º |
|
Cuadro 1.6. Parámetros adoptados por convenio para los gálibos de material rodante y de obstáculos |
||
Para el cálculo de los gálibos del material rodante y de implantación de obstáculos se considerarán los siguientes casos:
a) Vehículo circulando a la máxima velocidad
Se considerará el efecto de la insuficiencia de peralte en el cálculo de las secciones externas del vehículo, y adicionalmente en el cálculo de las secciones internas de los vehículos de caja inclinable.
Asimismo se considerará el efecto de la insuficiencia de peralte en la determinación del gálibo de implantación de obstáculos en el lado exterior de la curva.
b) Vehículo parado
Se considerará el efecto del peralte en el cálculo de las secciones internas del vehículo, así como en la determinación del gálibo de implantación de obstáculos en el lado interior de la curva.
En la figura 1.3 se muestra la comparación entre los diferentes gálibos considerados.
|
donde: 1. Perfil constructivo máximo del material. z Desplazamientos cuasiestáticos teniendo en cuenta: I 0 o D 0 Disimetría en exceso sobre 1.º (Imáx-I0) o (Dmáx-D0) en el caso de s>so y/o hc>hco E Reducción Ei o Ea 2.Contorno de referencia. S Saliente D Desplazamiento lateral. 3. Contorno de referencia más salientes. 4. Desplazamiento cuasiestático debido a (I-I0) o (D-D0) Para s=s0 y hc=hco 5. Lugar envolvente del material considerado cinemáticamente (envolvente cinemática). 6. Desplazamientos aleatorios laterales (M1+M2). 7. Gálibo límite de implantación de obstáculos. 8. Márgenes complementarios laterales M3b. 9. Gálibo nominal de implantación de obstáculos. Figura 1.3. Comparación entre los diferentes gálibos |
1.5 NOTACIÓN Y UNIDADES
La definición de los parámetros utilizados en las fórmulas así como sus unidades de medida se recoge en el anejo 2.
2.1 CONSIDERACIONES GENERALES
El gálibo del material rodante se obtendrá a partir de los contornos de referencia cinemáticos definidos en los apartados 2.7.1, 2.8.1 y 2.9.1 y de las reglas asociadas para el gálibo cinemático del apartado 2.2.
El contorno resultante define el perfil constructivo máximo del material rodante apto para circular, tanto en recta como en curva.
Dentro del gálibo del material rodante se incluyen las siguientes tolerancias de construcción del vehículo:
– 0,010 m, en la altura de las partes altas y bajas.
– 0,0025 m, en el semiancho del vehículo.
En el caso de tolerancias superiores a las indicadas, la diferencia deberá contabilizarse como una reducción adicional, en el cálculo del gálibo del material rodante.
2.2 REGLAS ASOCIADAS
Consisten en un conjunto de reducciones y ampliaciones a aplicar al contorno de referencia cinemático, que tienen en cuenta posibles desplazamientos del vehículo, respecto a su posición media, debidos a: desgastes, holguras, deformaciones, efectos de la suspensión, peraltes, inscripciones en curva o en acuerdos verticales, etc.
2.2.1 REDUCCIONES Y AMPLIACIONES A CONSIDERAR
Las reducciones y ampliaciones a considerar en la modificación del contorno de referencia cinemático serán las siguientes:
1. Reducciones verticales en las partes inferior y superior del contorno de referencia, para considerar posibles desplazamientos verticales debidos a:
a) Desgastes de los elementos de rodadura del vehículo.
b) Deformaciones de la estructura del vehículo.
c) Efecto de la suspensión.
d) Inscripción del vehículo en acuerdos verticales.
2. Reducciones del semiancho del contorno de referencia cinemático (bCR), para considerar los posibles desplazamientos cinemáticos laterales (Dplcin) debidos a:
a) Desplazamientos geométricos (dg) por inscripción en curva, entre el eje de simetría del vehículo y el de la vía.
b) Holguras laterales entre eje de ruedas y vía (wv).
c) Holguras laterales entre eje de ruedas y bastidor de bogie o entre eje de ruedas y caja, en vehículos sin bogie (q).
d) Holguras laterales entre bastidor de bogie y caja (w).
e) Desplazamientos cuasiestáticos (z1) debidos a un exceso (Do) o insuficiencia (Io) de peralte, para un coeficiente de flexibilidad de la suspensión s.
Este desplazamiento deberá aumentarse en aquellos vehículos cuyos valores de s o hc supongan un desplazamiento adicional, respecto al considerado en la determinación del gálibo de implantación de obstáculos para un exceso (Dmáx-Do) o insuficiencia de peralte (Imáx-Io), conlos valores de so y hco.
f) Desplazamientos (z2) por disimetría en exceso sobre 1.º, debida a eventuales tolerancias de construcción ó reglaje, o a reparto asimétrico de las cargas.
3. Ampliación del semiancho del contorno de referencia con los «salientes» (S) indicados en los apartados 2.7.2.4, 2.8.2.4 y 2.9.2.4, en función del radio de curva de inscripción del vehículo (R) y del ancho de vía (l).
No se tendrán en cuenta para el cálculo del gálibo del material rodante, aunque sí para el cálculo del gálibo de implantación de obstáculos, los desplazamientos, respecto a la posición media del vehículo en la vía, causados por:
a) Efectos cuasiestáticos laterales debidos a un exceso (D) o insuficiencia (I) de peralte comprendido entre D0 ó I0 y el máximo posible en cada caso, para un coeficiente de flexibilidad so.
b) Efectos cuasiestáticos verticales debidos a un exceso (D) o insuficiencia (I) de peralte comprendido entre D0 ó I0 y el máximo posible en cada caso, para un coeficiente de flexibilidad so.
c) Giros aleatorios del material rodante por disimetría ηo≤1.º debida a eventuales tolerancias de construcción ó reglaje (αsusp), o a reparto asimétrico de la carga (αc).
d) Giros aleatorios por oscilación del material rodante en su interacción dinámica con la vía, a causa de las irregularidades de ésta (αosc).
e) Efectos geométricos y cuasiestáticos debidos a defectos de alineación (Tvía), nivelación (TN) o peralte (TD) de la vía, respecto a su valor teórico.
f) Márgenes complementarios para reserva de infraestructura e incremento de la seguridad (M3b y M3h).
2.2.2 DESPLAZAMIENTOS VERTICALES
En este apartado se definen los desplazamientos verticales a considerar en la reducción de las partes altas y bajas del contorno de referencia.
2.2.2.1 Determinación de la altura mínima
La parte baja del gálibo del material rodante se dispondrá a una altura mínima sobre el plano de rodadura igual a la del contorno de referencia, más las reducciones (elevaciones) indicadas en este apartado. Estas reducciones contrarrestan posibles acercamientos entre la caja del vehículo y la vía, debidos a diferentes factores (descensos de la caja, inscripción del vehículo en acuerdos verticales, paso por frenos de vía, etc.).
2.2.2.1.1
Descenso de caja por desgaste de los elementos de rodadura (Usr,
![]() )
)
Se considerarán los descensos de caja debidos a los desgastes siguientes:
a) En ruedas (Usr): Se tomará el desgaste máximo correspondiente al tipo de vehículo que se esté considerando. En el caso de vehículos con sistema de compensación de altura previsto en su mantenimiento, se tomará el desgaste de rueda no compensado.
b) En equipos (resbaladeras, timonerías de freno, etc.): máximo desgaste admisible (![]() ).
).
c) En cajas de grasa: no se consideran desgastes.
2.2.2.1.2 Descenso por deformaciones de la estructura del vehículo (Flc)
Se considerarán los descensos de caja debidos a las deformaciones siguientes:
a) En ejes: no se consideran deformaciones.
b) En bastidor de bogie: no se consideran deformaciones.
c) En caja: no se considera la torsión. Únicamente se tienen en cuenta los desplazamientos verticales para los vagones (Flc), debidos al peso suspendido (con carga máxima), más una sobrecarga del 30%, a fin de tener en cuenta los esfuerzos dinámicos.
2.2.2.1.3 Descenso de las suspensiones (Aff)
Se considerarán los descensos de las suspensiones primarias y secundarias siguientes:
a) En muelles de acero y de caucho:
– Descenso bajo carga estática.
– Descenso adicional bajo carga dinámica.
– Descenso adicional debido a tolerancias de la flexibilidad.
b) En muelles neumáticos:
– Descenso total con suspensión deshinchada (incluida, en su caso, la suspensión de respaldo).
En el caso de muelles de acero y caucho, el descenso a considerar, en función del tipo de vehículo, será:
1. Locomotoras: descenso correspondiente al peso suspendido, más una sobrecarga del 30%.
2. Vagones: descenso total (vencimiento de la suspensión).
3. Coches, furgones, vagones especiales y material autopropulsado: descenso correspondiente al peso suspendido (con carga máxima), más una sobrecarga del 30%.
2.2.2.1.4 Inscripción en acuerdos verticales de vehículos no aptos para circular por lomos de asno, ni por frenos de vía en posición activa
La inscripción de cualquier vehículo en acuerdos verticales cóncavos o convexos produce unos desplazamientos geométricos (dgv).
En secciones internas: 
En secciones externas: 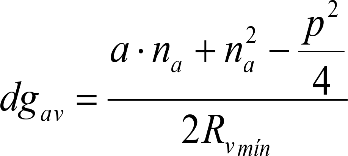
|
(1) Plano de rodadura (2) Contorno de referencia (3) Posición límite de los obstáculos humín: Altura mínima considerada para el desplazamiento vertical por inscripción en acuerdos verticales del material rodante por debajo del contorno de referencia homín: Altura mínima considerada para el desplazamiento vertical por inscripción en acuerdos verticales del material rodante por encima del contorno de referencia Rvmín: Radio de curvatura mínimo del acuerdo vertical Figura 2.1. Desplazamientos geométricos por inscripción en acuerdos verticales |
Los vehículos no aptos para circular por lomos de asno, ni por frenos de vía en posición activa, estarán diseñados para circular por acuerdos verticales cóncavos o convexos de radio Rv mín = 500 m, sin que ningún elemento, salvo las pestañas de las ruedas, quede bajo el plano de rodadura. En consecuencia, para contrarrestar el acercamiento entre el plano de rodadura y las partes bajas (h≤0,4m) del vehículo, éstas deberán elevarse las magnitudes indicadas a continuación:
a) En secciones internas del vehículo:

|
El signo [ ]>0 significa que cuando la expresión entre paréntesis es positiva, mantiene su valor, y cuando es negativa o nula, se toma cero. |
donde:
humin= 0,08 m para h<0,1 m y 0,10 m para h>0,1m
ei: Elevación a aplicar en las partes bajas del contorno de referencia, en secciones internas, en m.
a: Empate del vehículo, en m.
ni: Distancia en secciones internas, entre la sección considerada y el pivote (vehículos con bogies) o eje extremo (vehículos sin bogies) más próximo, en m.
p: Empate del bogie, en m.
b) En secciones externas del vehículo:

|
El signo [ ]>0 significa que cuando la expresión entre paréntesis es positiva, mantiene su valor, y cuando es negativa o nula, se toma cero. |
donde:
humin= 0,08 m para h<0,1 m y 0,10 m para h>0,1m
ea: Elevación a aplicar en las partes bajas del contorno de referencia, en secciones externas, en m.
na: Distancia en secciones externas, entre la sección considerada y el pivote (vehículos con bogies) o eje extremo (vehículos sin bogies) más próximo, en m.
2.2.2.1.5 Inscripción en acuerdos verticales de vehículos aptos para circular por lomos de asno y con mecanismos de frenado o maniobra
Estos elementos son habituales en las estaciones de clasificación. Se consideran los siguientes casos:
– Vehículos maniobrables por gravedad, aptos para circular por lomos de asno con frenos de vía en posición activa.
– Vehículos no maniobrables por gravedad, aptos para circular por lomos de asno con frenos de vía en posición no activa.
A los bogies y a su equipamiento se le aplicarán las mismas fórmulas que a los vehículos, reemplazando el valor de a (empate del vehículo) por p (empate del bogie) y el valor de p por cero.
a) Valores normales de incremento ei o ea de la altura mínima
Son de aplicación a:
– Vagones vacíos o cargados (se excluyen vagones de más de ocho ejes y cargados con mercancías peligrosas).
– Vehículos motores de maniobras utilizados en las estaciones de clasificación.
|
Figura 2.2. Reducciones ei o ea en acuerdos cóncavos o convexos |
|||||||||||||||
Tanto los vehículos maniobrables por gravedad, como los no maniobrables, estarán diseñados para circular por frenos de vía o por mecanismos de maniobra, situados:
‒ A una distancia x’ ≥ 3. m, del final de un acuerdo convexo de radio Rv ≥ 250 m. Afecta a las secciones internas de los vehículos.
‒ En acuerdos cóncavos de Rv ≥ 300 m o en sus proximidades. Afecta a las secciones externas de los vehículos.
En ambas secciones, los vehículos maniobrables por gravedad dispondrán de una altura mínima humín de 0,115/0,125 m sobre el plano de rodadura, que permita su paso por frenos de vía en posición activa. Análogamente, los no maniobrables por gravedad, dispondrán de una altura mínima humín de 0,08 m, que permita su paso por frenos de vía en posición no activa.
En consecuencia, las partes bajas se elevarán respecto al contorno de referencia correspondiente (0,115/0,125 m o 0,08 m) los valores ei o ea indicados a continuación.
a.1) Secciones internas
| Condiciones | Elevación normal a aplicar a h umin (m) |
|---|---|
Si: a ≤ 17,80 m y  |

|
Si: a ≤ 17,80 m y  |
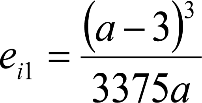
|
Si: a > 17,80 m y  |
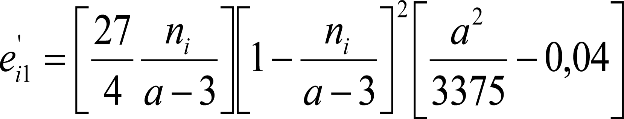
|
Si: a > 17,80 m y  |
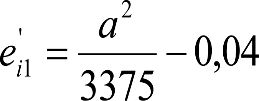
|
|
NOTA: Todos los valores del cuadro están expresados en metros. |
|
Además, los vehículos maniobrables por gravedad, estarán diseñados para circular por acuerdos verticales convexos de radio Rv ≥ 250 m, sin que ningún elemento, salvo las pestañas de las ruedas, quede bajo del plano de rodadura. Esta condición se traduce en una elevación:
|
Figura 2.3. Reducciones ei1 o e’i1 para secciones internas |
||||
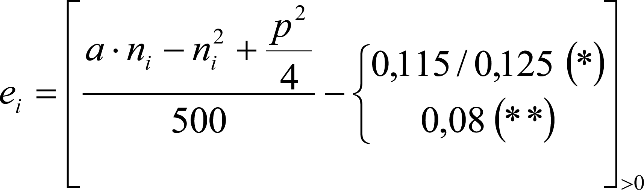
|
El signo [ ]>0 significa que cuando la expresión entre paréntesis es positiva, mantiene su valor, y cuando es negativa o nula, se toma cero. |
|
(*) Material apto para circular por frenos de vía en posición activa. (**) Material no apto para circular por frenos de vía en posición activa. |
a.2) Secciones externas (valores expresados en metros)
|
(1) (0,115 m/0,125 m) o 0,080 m Figura 2.4. Reducción ea para secciones externas |

b) Valores reducidos del incremento ei de la altura mínima en secciones internas
Únicamente son de aplicación a ciertos tipos de vagones, como los utilizados en transporte combinado (carretera/ferrocarril), que obligarían a aumentos significativos de la altura mínima. Su utilización puede requerir precauciones especiales.
Para estos vehículos se considera una longitud x’ = 5 m.
| Condiciones |
Elevación reducida a aplicar a humin (m) (solo para secciones internas) |
|---|---|
Si: a ≤ 15,80 m y 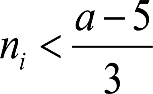 |
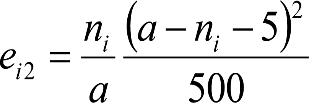
|
Si: a ≤ 15,80 m y 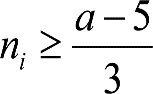 |
|
Si: a > 15,80 m y  |

|
Si: a > 15,80 m y  |
|
|
NOTA: Todos los valores del cuadro están expresados en metros. |
|
Además, los vehículos maniobrables por gravedad, estarán diseñados para circular por acuerdos verticales convexos de radio Rv ≥ 250 m, sin que ningún elemento, salvo las pestañas de las ruedas, quede bajo del plano de rodadura. Esta condición se traduce en una elevación:
|
Nota: Para bogies se reemplazará a por p. Figura 2.5. Reducciones ei2 o e’i2 para secciones internas |
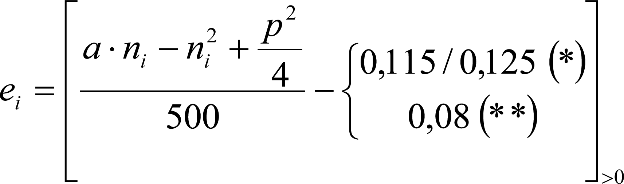
|
El signo [ ]>0 significa que cuando la expresión entre paréntesis es positiva, mantiene su valor, y cuando es negativa o nula, se toma cero. |
|
(*) Material apto para circular por frenos de vía en posición activa. (**) Material no apto para circular por frenos de vía en posición activa. |
En el cuadro 2.1 se indican los valores de ei1, e’i1, ei2 y e’i2 en función de a y de n.
|
Cuadro 2.1. Valores de ei1, e’i1, ei2 y e’i2(en mm), en función de a y n (en m) |
2.2.2.1.7 Descenso total
Para definir el descenso total del vehículo, se considerarán las zonas indicadas en la figura 2.6.
|
Figura 2.6. Zonas a considerar para el cálculo de los descensos. |
En el cuadro 2.2 se indican de forma resumida, y para cada zona A, B, C y D de la figura 2.6, los descensos a considerar en los cálculos de un caso genérico, los cuales deberán adaptarse a la arquitectura real del vehículo estudiado.
| Material motor, coches y autopropulsados | Vagones (una etapa de suspensión) | ||
|---|---|---|---|
| ZONA A | Desgaste de ruedas | Usr | Usr |
| Juego de las resbaladeras | ------ |
|
|
| Deformaciones de la estructura del vehículo | 0 | Flc | |
| Descenso de las suspensiones | Aff | Aff | |
| Acuerdos verticales | Ver apartados 2.2.2.1.4 y 2.2.2.1.5 | ||
| ZONA B | Desgaste de ruedas | Usr | Usr |
| Juego de las resbaladeras | ------ |
|
|
| Deformaciones de la estructura del vehículo | 0 | Flc | |
| Descenso de las suspensiones |
Ver nota |

|
|
| Acuerdos verticales | Ver apartados 2.2.2.1.4 y 2.2.2.1.5 | ||
| ZONA C | Desgaste de ruedas |
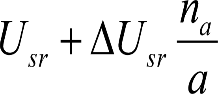
|

|
| Juego de las resbaladeras | ------ |
|
|
| Deformaciones de la estructura del vehículo | 0 | Flc | |
| Descenso de las suspensiones |

|

|
|
| Acuerdos verticales | Ver apartados 2.2.2.1.4 y 2.2.2.1.5 | ||
| ZONA D | Desgaste de ruedas |

|
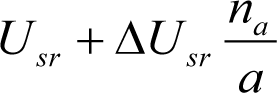
|
| Juego de las resbaladeras | ------ |
|
|
| Deformaciones de la estructura del vehículo | 0 | Flc | |
| Descenso de las suspensiones |
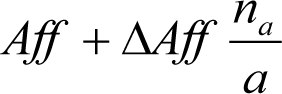
|
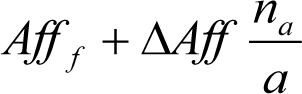
|
|
| Acuerdos verticales | Ver apartados 2.2.2.1.4 y 2.2.2.1.5 | ||
|
NOTAS |
‒ El valor de s incluye posibles descensos residuales de las suspensiones. ‒ Según la arquitectura de la suspensión el parámetro b1 puede reemplazarse por el b2 en las fórmulas indicadas ‒ Aff: Descenso de las suspensiones (incluyendo tolerancias de los muelles), según apartado 2.2.2.1.3. ‒ ΔAff: Diferencia de descenso de las suspensiones: ∙ En sentido longitudinal (zonas C y D) se toma la diferencia de descenso entre los dos bogies. El primero sometido a la máxima carga estática y el segundo con el descenso (Aff) definido en 2.2.2.1.3. ∙ En sentido transversal (zonas B y C), se toma la diferencia de descenso entre los dos lados del vehículo. Uno sometido a la máxima carga estática y el segundo con el descenso (Aff) definido en 2.2.2.1.3. ‒ Usr: Diferencia entre el radio nominal y el radio mínimo admitido por operaciones de reperfilado. ‒ ΔUsr: Diferencia máxima admisible entre el radio de las ruedas de los dos bogies (vehículo de bogies) o entre las ruedas de los dos ejes (vehículo de ejes), debido a operaciones de reperfilado. ‒ Flc: Descenso por deformaciones de la estructura del vehículo, según apartado 2.2.2.1.2. ‒ b: Distancia desde cualquier punto del contorno del vehículo a su eje de simetría, medida en una sección transversal, paralelamente al plano de rodadura. Corresponde al semiancho del vehículo en ese punto. ‒ b1: Semidistancia entre los muelles de la suspensión primaria, medida en una sección transversal, paralelamente al plano de rodadura. ‒ b2: Semidistancia entre los muelles de la suspensión secundaria, medida en una sección transversal, paralelamente al plano de rodadura. |
||
|
Cuadro 2.2. Descensos a tener en cuenta en el cálculo de la altura mínima |
|||
2.2.2.2 Determinación de la altura máxima
La parte alta del gálibo del material se dispondrá a una altura máxima sobre el plano de rodadura igual a la del contorno de referencia, menos las reducciones indicadas en este apartado.
2.2.2.2.1 Elevación por deformación de la estructura del vehículo
Las contraflechas longitudinales de construcción no se tendrán en cuenta, salvo en el caso de los vagones.
2.2.2.2.2 Extensión de las suspensiones
Para cada nivel de la suspensión, se considerará una extensión de 0,010 m, o bien la obtenida mediante un cálculo específico.
No se considerará la componente vertical de los desplazamientos cuasiestáticos por considerarse despreciable (causados por D0 e I0), ni de los fenómenos aleatorios debidos a desviaciones de peralte (TD), disimetrías (η0) o irregularidades de la vía (αosc).
2.2.2.2.3 Inscripción en acuerdos verticales de R v ≥ 500 m
Los vehículos deberán disminuir su altura en las magnitudes indicadas a continuación:
a) En secciones internas:

b) En secciones externas:
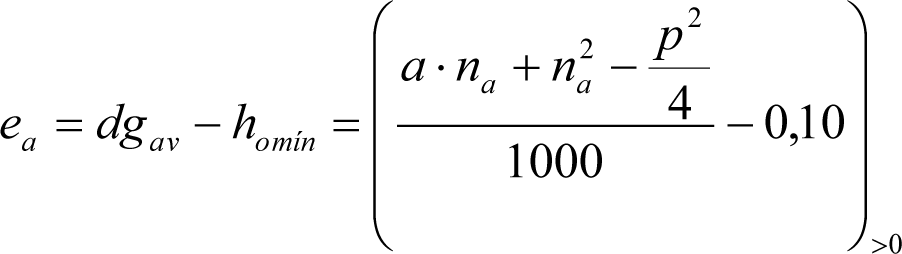
2.2.3 DESPLAZAMIENTOS HORIZONTALES
2.2.3.1 desplazamiento geométrico (dg) por inscripción en curva
El desplazamiento horizontal, en una curva de radio R, entre los ejes de simetría del vehículo y de la vía, varía con la sección transversal del vehículo considerada, por lo que se calculará en las secciones más desfavorables.
En secciones internas:

En secciones externas:
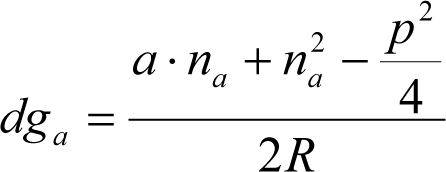
En ambas fórmulas, el término ![]() es la parte del desplazamiento geométrico debido a la inscripción en curva de los bogies.
es la parte del desplazamiento geométrico debido a la inscripción en curva de los bogies.
En vehículos con bogies pero sin pivote, se tomará como pivote ficticio, el punto de corte del eje longitudinal del bogie con el de la caja, considerando el vehículo inscrito en una curva de R=150 m (anchos ibérico y estándar europeo) o R=80 m (ancho métrico), y con las holguras uniformemente repartidas.
Siendo y la distancia entre el pivote ficticio y el centro geométrico del bogie (a igual distancia de ejes extremos) y p’ el empate del bogie portador (en vehículos con un bogie motor y otro portador), se reemplazará en las fórmulas anteriores p2 por (p2-y2) y p’2 por (p’2-y2).
|
Figura 2.7. Desplazamiento geométrico del vehículo por inscripción en curva |
|
Figura 2.8. Desplazamiento geométrico del bogie por inscripción en curva |
2.2.3.2 holguras laterales
En este apartado se definen las holguras laterales de los elementos del vehículo que ponen en contacto la caja con la vía.
2.2.3.2.1 holgura lateral entre eje de ruedas y vía (w v )
La holgura lateral entre eje de ruedas y vía, a cada lado del vehículo, respecto a su posición media, será:

siendo:
l: ancho de vía.
l = lmáx = lN+ sobre ancho máximo = lN +0,03 (caso general).
l = lN (casos de secciones internas en curva, tanto para vehículos remolcados con dos bogies portadores o cuasiportadores, como para vagones con bogies).
d: distancia mínima entre las caras activas de las pestañas de las ruedas de un eje, medida a 10 mm por debajo del círculo de rodadura, con ambas pestañas al límite de desgaste.
|
(1) Holgura lateral entre eje de ruedas y vía (2) Eje de la vía (3) Posición central del eje de ruedas del vehículo (4) Desplazamiento transversal relativo entre el eje de ruedas y el eje de la vía: Figura 2.9. Holgura lateral entre eje de ruedas y vía |
2.2.3.2.2 Holgura lateral entre eje de ruedas y bastidor del bogie o entre eje y caja, en vehículos sin bogies (q)
La holgura lateral q entre eje de ruedas y bastidor del bogie será la suma de las holguras entre eje y caja de grasa, y entre ésta y las placas de guarda o el bastidor del bogie, medidas a partir de su posición media y a cada lado, con todos los elementos al límite de desgaste.
En vehículos sin bogies esta holgura se da entre el eje y la caja del vehículo.
2.2.3.2.3 Holgura lateral entre bastidor del bogie y caja (w)
Esta holgura se da entre la estructura soporte de los elementos de rodadura (bogie, rodal, etc.) y la caja del vehículo.
En los vehículos convencionales esta holgura se produce entre los pivotes de los bogies y las vigas bailadoras. Para vehículos sin pivote, es la holgura de la caja respecto al bastidor del bogie. Se mide desde la posición media y a cada lado.
Es función del radio de la curva R y de la posición de rodadura del vehículo sobre la vía.
En general, w no es constante, por lo que cabe distinguir entre:
w∞ para vía en recta.
wi(R) para curva de radio R, y del lado interior de la curva.
wa(R) para curva de radio R, y del lado exterior de la curva.
|
(1) Holgura lateral q (2) Holgura lateral w (3) Posición central del eje de ruedas del vehículo Figura 2.10. Holguras laterales q y w |
2.2.3.2.4 Posición de rodadura del vehículo sobre la vía y factores de desplazamiento (A)
La aplicación de las holguras anteriores al cálculo de las reducciones del semiancho del contorno de referencia de un vehículo, tanto en secciones internas Ei, como externas Ea, requiere multiplicarlas, en determinados casos, por unos factores de desplazamiento Awv, Aq, Aw, Ap, específicos para cada tipo de holgura.
Dichos factores, son función de la posición de inscripción de los ejes de rodadura del vehículo sobre la vía, lo que a su vez depende de la tipología de éstos (ejes independientes, bogies motores, bogies portadores, etc.).
Por ello, es necesario considerar las posiciones más desfavorables.
En el cuadro 2.4 se definen, para distintos tipos de vehículo y posiciones de rodadura, los factores de desplazamiento a aplicar a cada tipo de holgura y al factor ![]() , en el caso de vehículos con bogies. Para configuraciones no representadas en el cuadro, se seleccionará la posición de rodadura más desfavorable.
, en el caso de vehículos con bogies. Para configuraciones no representadas en el cuadro, se seleccionará la posición de rodadura más desfavorable.
En el caso de vehículos articulados, se elegirá la posición de rodadura correspondiente a vehículos convencionales de dos bogies.
Los vehículos de ruedas independientes pueden no respetar las posiciones de rodadura indicadas en el cuadro 2.4.
En el caso de los vehículos autopropulsados, los bogies se clasifican según el coeficiente de adherencia de los ejes en arranque y marcha (μ), definidos en el cuadro 2.3:
| Tipo de bogie | Coeficiente de adherencia de los ejes del bogie (μ) |
|---|---|
| Bogie motor | μ ≥ 0,2 |
| Bogie cuasi-portador | 0 < μ < 0,2 |
| Bogie portador | μ = 0 |
| Bogie mixto | Un eje con μ < 0,2 y otro con μ ≥ 0,2 |
|
Cuadro 2.3. Coeficiente de adherencia de los vehículos autopropulsados |
|
El coeficiente de adherencia de un eje se define como:
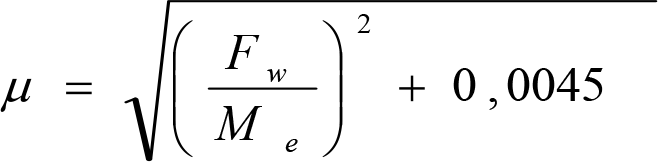
donde:
Fw: Fuerza máxima de tracción en el contacto entre las llantas del eje del vehículo y el carril, en kN.
Me: Carga por eje, en kN.
|
|
|
|
|
donde: a: Empate del vehículo. n: Distancia entre la sección considerada y el pivote (vehículos con bogies) o eje extremo (vehículos sin bogies) más próximo. p: Empate del bogie. p’: Empate del bogie portador en vehículos con un bogie motor y otro portador. w: Holgura lateral entre bastidor de bogie y caja. w∞: Valor de w, en el caso de recta. wi(R): Valor de w, en el lado interior de una curva de radio R. wa(R): Valor de w, en el lado exterior de una curva de radio R. w’∞: Valor de w, en el caso de recta, para el bogie portador en un vehículo con un bogie motor y otro portador. w’i(R): Valor de w, en el lado interior de una curva de radio R, para el bogie portador en un vehículo con un bogie motor y otro portador. w’a(R): Valor de w, en el lado exterior de una curva de radio R, para el bogie portador en un vehículo con un bogie motor y otro portador. Cuadro 2.4. Factor de desplazamiento en función del tipo de vehículo y de su posición de rodadura sobre la vía |
2.2.3.3 Desplazamientos cuasiestáticos (z1) por exceso o insuficiencia de peralte
Un vehículo circulando por una curva de radio R a una velocidad v, está sometido a una aceleración centrífuga ![]() , que es preciso reducir mediante un peralte D.
, que es preciso reducir mediante un peralte D.
La diferencia entre la aceleración centrífuga y la reducción por peralte, se expresa como aceleración centrífuga no compensada (γc’) o como insuficiencia de peralte (I):
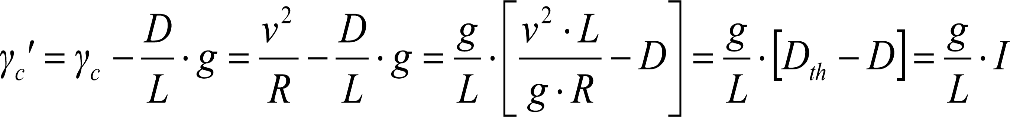
siendo:
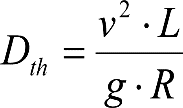 el peralte de equilibrio
el peralte de equilibrio
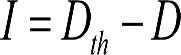 la insuficiencia de peralte.
la insuficiencia de peralte.
Con I=0 el peralte compensa la totalidad de la aceleración centrífuga, por lo que la suspensión no está sometida a ninguna solicitación lateral.
Con I>0, el peralte no compensa la totalidad de la aceleración centrífuga, por lo que la suspensión inclina la caja del vehículo hacia el exterior de la curva.
Con I<0, hay un exceso de peralte, por lo que la suspensión inclina la caja del vehículo hacia el interior de la curva.
Para un peralte D dado, la máxima insuficiencia de peralte se produce cuando el vehículo circula a la máxima velocidad permitida en esa sección.
Análogamente, el máximo exceso de peralte se produce con el vehículo parado sobre la curva (V=0).
En cualquiera de los casos anteriores, la caja del vehículo sufre simultáneamente los siguientes movimientos:
∙ Un desplazamiento lateral paralelo al plano de rodadura, de forma que su eje central se sitúa en la posición XX.
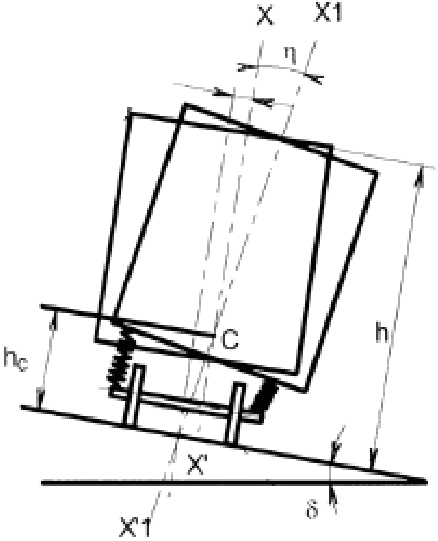
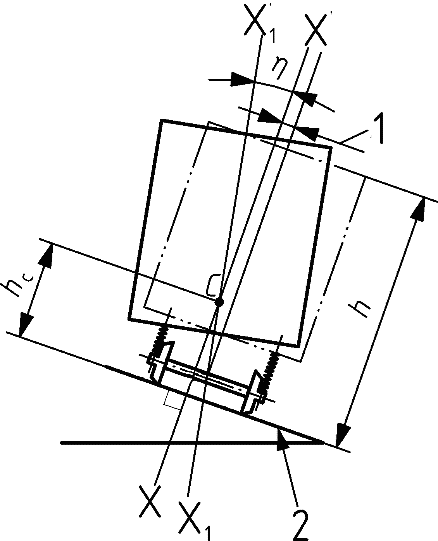
∙ Un giro tal que su eje central adopta la posición X1X1. El giro de la caja se realiza alrededor de un punto situado en la intersección de los ejes XX y X1X1 denominado centro de balanceo (C), situado a una altura hc, respecto al plano de rodadura, que es prácticamente independiente de la magnitud de la fuerza transversal aplicada.
La posición del centro de balanceo varía en función de que el vehículo esté: parado en vía peraltada; circulando en curva con insuficiencia de peralte; o parado en vía sin peralte.
|
|

|
| Vehículo parado en vía peraltada | Vehículo circulando en curva con insuficiencia de peralte | Vehículo con disimetría parado en vía sin peralte |
|
(1) Desplazamiento transversal de la caja del vehículo (2) Plano de rodadura Figura 2.11 Giro de un vehículo sobre su centro de balanceo |
||
Se denomina coeficiente de flexibilidad de un vehículo al valor positivo: ![]()
Siendo:
η: giro de la caja respecto al centro de balanceo (C), del vehículo parado sobre vía peraltada, en ausencia de disimetrías y de rozamientos en la suspensión, debido a la flexión de las suspensiones.
![]() :ángulo que forma el plano de rodadura con el plano horizontal.
:ángulo que forma el plano de rodadura con el plano horizontal.
|
(1) Perpendicular al plano de rodadura (2) Eje del vehículo por efecto de la flexibilidad de las suspensiones Figura 2.12. Giro de la caja debido a la flexibilidad de las suspensiones |
Un vehículo sometido a un exceso (Do) o insuficiencia (Io) de peralte, gira alrededor de su centro de balanceo (C) y se inclina respecto al plano de rodadura un ángulo:  . El desplazamiento lateral de un punto del vehículo situado a una altura h, debido a D0 o I0, será:
. El desplazamiento lateral de un punto del vehículo situado a una altura h, debido a D0 o I0, será:

siendo:
hc: altura del centro de balanceo respecto el plano de rodadura.
L: distancia entre los círculos de rodadura de un eje.
Do, Io: exceso e insuficiencia de peralte considerados en la determinación del gálibo de material rodante.
Los excesos (Dmáx-Do) e insuficiencias (Imáx-Io) de peralte correspondientes a la diferencia entre los máximos admitidos para cada ancho de vía (Dmáx, Imáx) y los considerados para el gálibo del material rodante (Do, Io), se tienen en cuenta en la determinación del gálibo de implantación de obstáculos, pero suponiendo que los vehículos tienen un coeficiente de flexibilidad so y una altura del centro de balanceo hco.
Por tanto, deberá corregirse el valor de z1, en el caso de vehículos cuyos valores de s y hc supongan un desplazamiento adicional respecto al considerado en la determinación del gálibo de implantación de obstáculos (exceso de peralte Dmáx-Do o insuficiencia de peralte Imáx-Io, conlos valores de so y hco). Esto podría ocurrir si s> so y/o hc < hco.
En consecuencia, el desplazamiento lateral, debido a un exceso de p eralte, de un punto del vehículo situado a una altura h, será:

Análogamente se calcularía el desplazamiento debido a una insuficiencia de peralte, sustituyendo D y D0 por I e I0.
2.2.3.4 Desplazamientos cuasiestáticos (z2) por disimetría
Un vehículo parado sobre una vía horizontal, y en ausencia de rozamiento, puede presentar una disimetría debida a un defecto de construcción, a un reglaje imperfecto o a un reparto desigual de cargas, por lo que considerando la flexibilidad de la suspensión, su caja girará alrededor del centro de balanceo (C) un ángulo:
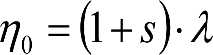
donde:
λ: Disimetría del vehículo (ángulo que forma la vertical con la línea que une los centros de gravedad y de rotación) sin considerar la flexibilidad de las suspensiones.
|
Figura 2.13. Disimetría del vehículo |
El desplazamiento lateral debido a η0, de un punto situado a una altura h será:
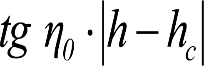
Y el desplazamiento lateral debido al exceso sobre 1.º del ángulo η0, será:
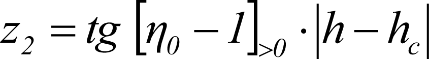
|
El signo [ ]>0 significa que cuando la expresión entre paréntesis es positiva, mantiene su valor, y cuando es negativa o nula, se toma cero. |
2.2.3.5 Salientes
El saliente es lo que sobresaldría lateralmente, respecto al contorno de referencia, un vehículo de referencia (tipo) al inscribirse en curva, considerando sus holguras correspondientes. Se obtiene como suma de los siguientes parámetros:
∙ Diferencia entre los semianchos del contorno de referencia y del vehículo de referencia.
∙ Desplazamiento geométrico por inscripción en curva del vehículo de referencia.
∙ Holguras del vehículo de referencia (wvr, qr y wr) afectadas por sus correspondientes factores de desplazamiento (Ai).
∙ Desplazamientos cuasiestáticos del vehículo de referencia.
En la figura 2.14 se muestra el espacio ocupado por los salientes.
|
(1) Vehículo de referencia (2) Contorno de referencia (3) Saliente hacia el exterior Sa de la curva (4) Saliente hacia el interior Si de la curva Figura 2.14. Salientes |
Los salientes a aplicar para cada ancho de vía, en función del gálibo, se definen en los apartados 2.7.2.4, 2.8.2.4 y 2.9.2.4.
2.3 CÁLCULO DEL GÁLIBO DEL MATERIAL RODANTE
La determinación de los desplazamientos verticales del apartado 2.2.2, permite definir la altura mínima de las partes bajas y la altura máxima de las partes altas del gálibo del material rodante.
Análogamente, la determinación de los desplazamientos horizontales del apartado 2.2.3, junto con el saliente correspondiente, permite calcular la reducción del semiancho del contorno de referencia, a fin de obtener el gálibo del material rodante.
El perfil constructivo del vehículo deberá estar contenido dentro del gálibo del material rodante.
|
(1) Contorno de referencia (2) Gálibo del material rodante (perfil constructivo máximo del material) (3) Perfil constructivo del vehículo (4) Perfilado Ei y Ea: reducciones de la semianchura del contorno de referencia en secciones internas y externas, respectivamente. Figura 2.15. Espacio disponible para la construcción del vehículo |
El semiancho máximo del vehículo (bveh) a una altura h sobre el plano de rodadura, se obtendrá añadiendo al contorno de referencia cinemático (bCR) el correspondiente saliente cinemático (S) y restando los desplazamientos cinemáticos (Dplcin).

Las reducciones del semiancho del contorno de referencia en secciones internas (Ei) y externas (Ea) serán, respectivamente:
 , siendo: , siendo: 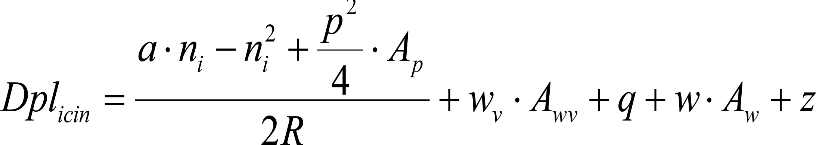 |
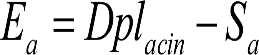 , siendo: , siendo: 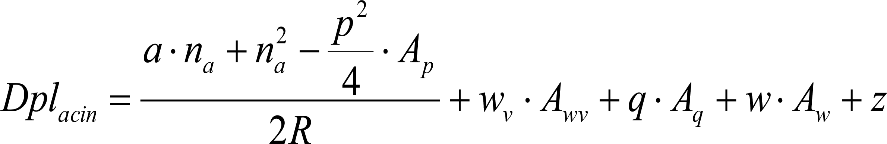 |
dónde:
Si y Sa: Salientes en secciones internas y externas, respectivamente.
La suma de los desplazamientos (z) debidos al exceso de peralte Do con sus correcciones correspondientes, más el desplazamiento debido a disimetría en exceso de 1.º, será:
a) Caso general:
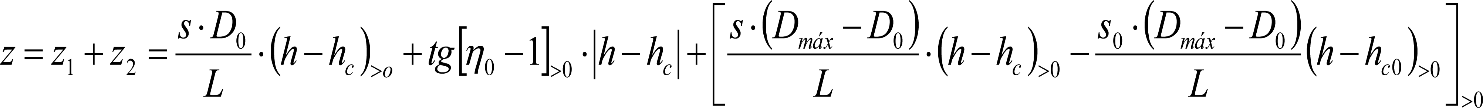
b) Vagones equipados con bogies:
Se distinguen dos casos, en función de la holgura de las resbaladeras (J):
b.1) Si J ≤ 5 mm, se supone que esta holgura está englobada en la disimetría η0=1.º, por lo que:
![]()
b.2) Si J > 5 mm, hay que considerar un giro suplementario de la caja:

dónde:
J: Holgura de las resbaladeras, en m.
bG: Semidistancia entre ejes de resbaladera, medida en una sección transversal, paralelamente al plano de rodadura, en m.
Este giro de la caja α produce un desnivelado de la suspensión que se traduce en un giro adicional de la caja de valor ![]() , por lo que el giro total de ésta será:
, por lo que el giro total de ésta será: 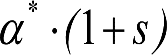 .
.
Añadiendo este término a la ecuación del caso general, se tiene:
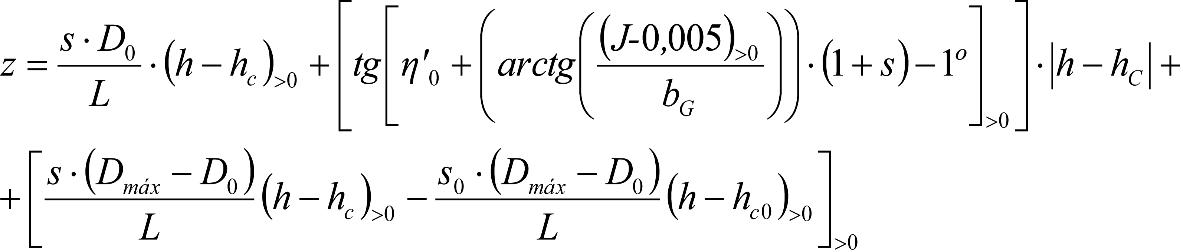
dónde η’0 es la disimetría para el caso de J = 5 mm.
Se consideran los siguientes casos particulares:
a) 
b) 
c) 
d) Para las partes del vehículo no suspendidas: z=0
Análogamente se obtendría el valor de z para el caso de insuficiencia de peralte más disimetría, sustituyendo Dmáx y Do por Imáx e Io.
Las fórmulas de reducción para diferentes tipos de gálibos y de vehículos, se definen en los apartados 2.7.3, 2.8.3 y 2.9.3.
2.4 CÁLCULO DEL GÁLIBO DE VEHÍCULOS DE CAJA INCLINABLE (VCI)
2.4.1 Sistemas de inclinación de las cajas
Hay dos sistemas básicos:
a) Activo. La inclinación de la caja se realiza a través de unos mecanismos que actúan en función del radio de la curva y de la velocidad de circulación (p.ej. TRD BASCULANTE). Generalmente éstos mecanismos están situados por encima de la suspensión secundaria, aunque en algunos casos se sitúan entre la suspensión primaria y la secundaria.
b) Pasivo. La inclinación se produce mediante un movimiento pendular natural o equivalente alrededor de un centro de rotación situado por encima del centro de gravedad de la caja (p.ej. TALGO).
|
SISTEMA ACTIVO La caja sufre un giro cuasiestático (1) bajo la acción de la fuerza centrífuga, pero el sistema impone la inclinación final de la caja (2). La fig. 2.16 representa el principio de inclinación activa de un vehículo. |
SISTEMA PASIVO La caja gira, proporcionalmente a la insuficiencia de peralte, bajo la acción de la fuerza centrífuga. La fig. 2.17 representa el principio de inclinación natural o pasiva de un vehículo. |
|
Figura 2.16. |
Figura 2.17. |
|
SISTEMA ACTIVO La fig. 2.18 representa el esquema de un caso particular de inclinación activa. El movimiento efectivo de la caja se puede descomponer en dos rotaciones: La 1, debida a la fuerza centrífuga, hacia el exterior de la curva, alrededor del centro de balanceo (C), y la 2, impuesta por el sistema, contraria a la anterior, alrededor de un punto situado a una altura ho respecto al plano de rodadura. |
SISTEMA PASIVO La fig. 2.19 representa el esquema de un caso particular de inclinación pasiva. El movimiento efectivo de la caja se puede descomponer en dos rotaciones debidas a la fuerza centrífuga: La 1, hacia el exterior de la curva, alrededor del centro de balanceo (C), y la 2, alrededor de un punto situado a una altura ho respecto al plano de rodadura. |
|
Figura 2.18. |
Figura 2.19. |
2.4.2 Condiciones de partida
El constructor de un VCI deberá:
a) Realizar un informe de los criterios adoptados y de los dispositivos en los que se sustenta la seguridad.
b) Comprobar que el vehículo respeta el gálibo del material rodante de los vehículos convencionales, para cada situación operativa del vehículo, eligiendo la más desfavorable en cada caso.
c) Estudiar posibles situaciones de avería del vehículo en las que éste pueda rebasar el gálibo del material rodante de los vehículos convencionales. Según la importancia de sus efectos, el Operador ferroviario podrá adoptar medidas particulares a nivel de explotación (p.ej.: alarmas, avisos al maquinista, etc.).
Las comprobaciones del gálibo del material rodante se realizarán a partir de los contornos de referencia y de las fórmulas de reducción de los apartados 2.7 y 2.8, con las indicaciones dadas en el apartado 2.4.3. Dichas comprobaciones se realizarán, como se ha indicado en el punto b), para las diferentes situaciones operativas del vehículo, eligiendo las más desfavorables. En particular, se analizarán:
∙ SITUACIÓN 1): Vehículo circulando en curva con insuficiencia de peralte máxima (inclinación máxima de la caja). Se calcularán secciones externas e internas del vehículo. Cuando no existan secciones externas (p.ej. en vehículos articulados) se calcularán en las secciones más próximas al eje de rodadura.
∙ SITUACIÓN 2): Vehículo detenido en curva. En este caso los sistemas de inclinación de la caja están desactivados, por lo que la situación es análoga a la de un vehículo clásico y se analizará conforme a los apartados 2.7 ó 2.8. Se calcularán únicamente secciones internas.
Para ciertos vehículos TALGO, no existe inclinación cuasiestática zp debida a la flexibilidad (s=0).
En el anejo 5 se incluyen algunos ejemplos de aplicación.
2.4.3 REGLAS ASOCIADAS
2.4.3.1 Holguras laterales
Las holguras a considerar, con sus signos, en la verificación de las distintas situaciones operativas de los VCIs, en los lados interior y exterior de la curva se indican en el cuadro 2.5.
| Wv | q | w (*) | ||
|---|---|---|---|---|
| SITUACIÓN 1 | Lado exterior de la curva |
|
+ q | + w a(R) |
| Lado interior de la curva (caso de sistemas activos con bogies) | 0 (**) | 0 (**) | - w a(R) | |
| SITUACIÓN 2 | Lado interior de la curva |
|
+ q | + w i(R) |
|
(*) w se mide a una altura hc sobre el plano de rodadura. Para un mismo vehículo, y en función de la tecnología de inclinación, puede tener valores diferentes en cada situación operativa. En los sistemas pasivos tipo TALGO el valor de w a considerar será el w* indicado dentro de este apartado 2.4.3.1. (**) Se adopta una posición neutra debido a que unas veces las ruedas recorren la curva con la pestaña en contacto con el carril exterior, y otras veces no. |
||||
|
Cuadro 2.5. Holguras a considerar en las situaciones de comprobación de VCIs |
||||
En el caso particular de los vehículos tipo TALGO, con ruedas independientes, la holgura w* se calculará mediante la fórmula:
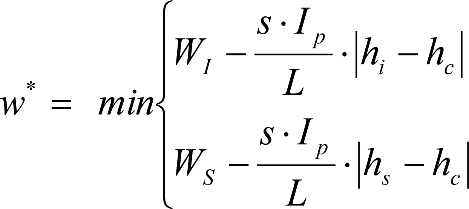
siendo:
WI: Holgura entre la caja y la estructura del vehículo en el tope lateral inferior.
WS: Holgura entre la caja y la estructura del vehículo en el tope lateral superior.
hi: Altura del tope inferior del sistema de basculación de la caja, respecto al plano de rodadura.
hs: Altura del tope superior del sistema de basculación de la caja, respecto al plano de rodadura.
Las características del sistema de inclinación para estos vehículos se indican en la figura 2.20.
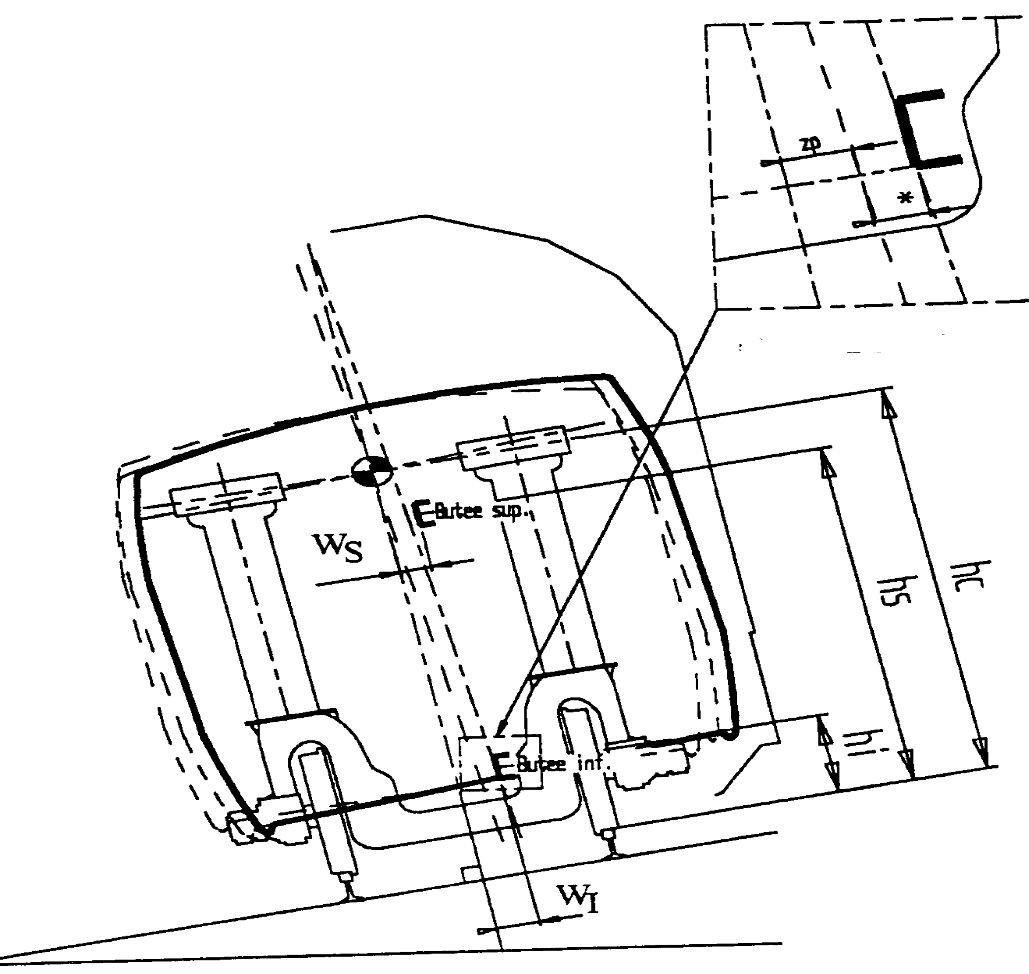
|
Cuando el vehículo circula sobre una vía en curva con una Ip>0, la caja gira alrededor del centro de balanceo un ángulo correspondiente a Ip, (línea de trazos) y además, se desplaza lateralmente hasta contactar, en su caso, con uno de los topes (línea mixta). En la figura se indica con un * la holgura disponible hasta el contacto con el tope. |
|
Figura 2.20. Características del sistema de inclinación de vehículos tipo TALGO, con ruedas independientes |
|
Los valores WS(R), WI(R), y en consecuencia w*, pueden ser distintos en recta o en curva, y en secciones internas o externas, por lo que hay que distinguir entre:
w*∞, WI∞, WS∞ para vía en recta.
w*i(R), WI,i(R), WS,i(R) para curva de radio R, y del lado interior de la curva.
w*a(R), WI,a(R), WS,a(R) para curva de radio R, y del lado exterior de la curva.
2.4.3.2 Desplazamientos cuasiestáticos (zp) en los VCI
Los VCI pueden circular con insuficiencias de peralte (Ip) muy superiores a las de los vehículos convencionales (Imáx) y a las consideradas por el Administrador de la Infraestructura ferroviaria (Ic). Así, para determinar los desplazamientos cuasiestáticos zp de los VCI, hay que modificar las fórmulas del apartado 2.3.
Las fórmulas de este apartado son aplicables a Ip>Ic.
En cada situación operativa a verificar, el constructor del VCI analizará con detalle la obtención del término zp a utilizar en las fórmulas de reducción, teniendo en cuenta los diferentes topes, centros de balanceo, etc., del sistema.
En SITUACIÓN 1:
a) En el lado exterior de la curva, los desplazamientos cuasiestáticos zp, a considerar en el cálculo del gálibo del material rodante, para una insuficiencia de peralte Ip, serán la diferencia entre los totales, ztotal, y los considerados por el Administrador de la Infraestructura en la obtención del gálibo de implantación de obstáculos, qsi/a, es decir:
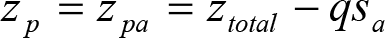 , siendo:
, siendo: 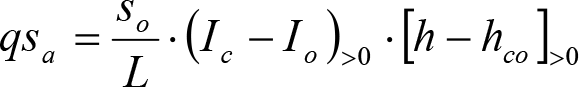
b) En el lado interior de la curva, los desplazamientos cuasiestáticos zp, a considerar en el cálculo del gálibo del material rodante coincidirán con los totales, ztotal, ya que el Administrador de la Infraestructura no considera ningún desplazamiento cuasiestático en el gálibo de implantación de obstáculos, 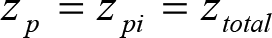
El valor de ztotal, se obtendrá de los siguientes cuadros:
| SITUACIÓN 1 para VCIs con sistemas de inclinación activos cuyo mecanismo de giro impuesto por el sistema esté situado por encima de la suspensión secundaria, (el giro β no afecta a los desplazamientos cuasiestáticos causados por la flexibilidad de las suspensiones) y para VCIs con sistemas de inclinación pasivos. | |
|
∙ Lado exterior de la curva en sistemas activos con mecanismo de giro situado por encima de la suspensión secundaria. ∙ Lado interior de la curva en sistemas pasivos. |
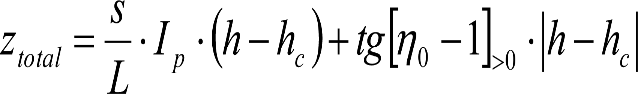
|
|
∙ Lado interior de la curva en sistemas activos con mecanismo de giro situado por encima de la suspensión secundaria. ∙ Lado exterior de la curva en sistemas pasivos. |
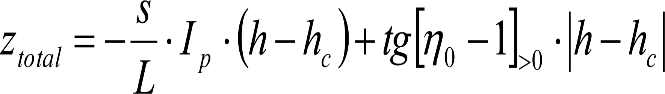
|
| SITUACIÓN 1 para VCIs con sistemas de inclinación activos cuyo mecanismo de giro impuesto por el sistema esté situado entre la suspensión primaria y la secundaria (p.ej. TRD Basculantes, en los que el giro β afectará a los desplazamientos cuasiestáticos causados por la flexibilidad de la suspensión secundaria) | |
|
a) Lado exterior de la curva en sistemas activos con mecanismo de giro situado entre las suspensiones primaria y secundaria.
|
|
|
b) Lado interior de la curva en sistemas activos con mecanismo de giro situado entre las suspensiones primaria y secundaria.
|
|
|
donde: anccaja: Aceleración centrífuga no compensada a nivel de caja, en m/s2. ancvía: Aceleración centrífuga no compensada a nivel de vía, en m/s2. hccaja: Altura del centro de rotación de la suspensión secundaria, en m. hcvía: Altura del centro de rotación de la suspensión primaria, en m. |
|
En SITUACIÓN 2:
Los desplazamientos cuasiestáticos zp serán los correspondientes a los vehículos clásicos definidos en el apartado 2.3, es decir:
![]()
Los valores de s y hc pueden variar en función de la situación operativa a verificar.
Los elementos de los VCI no asociados a la caja (p.ej. bogies y ciertos pantógrafos), no están afectados por su inclinación, por lo que sufrirán una aceleración no compensada superior a la admitida. En consecuencia, el valor de zp será: 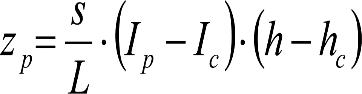
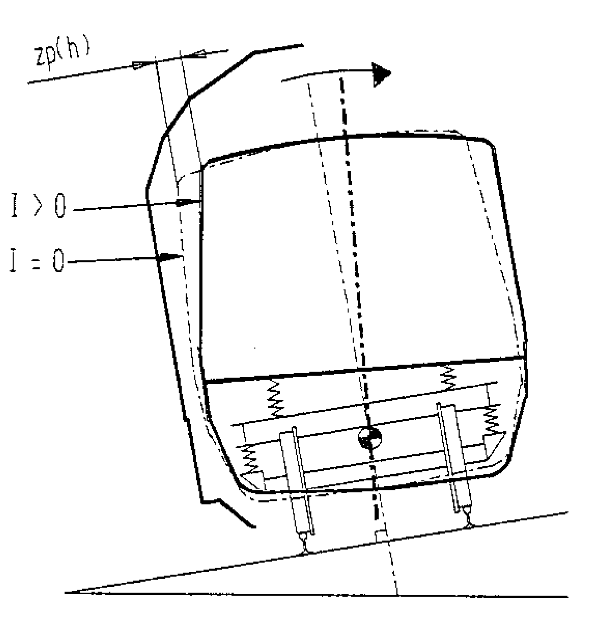
2.4.3.2.1 SITUACIÓN 1. Lado interior de la curva.
Las figuras 2.21 y 2.22 representan el giro de la caja del vehículo debido a una insuficiencia Ip>Ic>0 (a partir de la posición I=0), en función del sistema de inclinación de la caja.
|
SISTEMA ACTIVO La caja gira hacia el exterior de la curva. Los mayores desplazamientos se dan en su parte superior. |
SISTEMA PASIVO La caja gira hacia el interior de la curva. Los mayores desplazamientos se dan en su parte inferior. |
|
|
|
Nota: No se representa la inclinación impuesta por el sistema. Figura 2.21. |
Figura 2.22. |
|
Considerando el contorno de referencia del lado interior de la curva, los puntos del vehículo situados a una altura h>hc, se alejan del mismo, es decir, el desplazamiento ztotal <0. Lo contrario ocurre en los puntos situados a una altura h<hc. |
Considerando el contorno de referencia del lado interior de la curva, los puntos del vehículo situados a una altura h>hc se aproximan al mismo, es decir, el desplazamiento ztotal >0. Lo contrario ocurre en los puntos situados a una altura h<hc. |
|
Para una insuficiencia de peralte Ip>Ic, los desplazamientos cuasiestáticos serán:
|
Para una insuficiencia de peralte Ip>Ic, los desplazamientos cuasiestáticos serán:
|
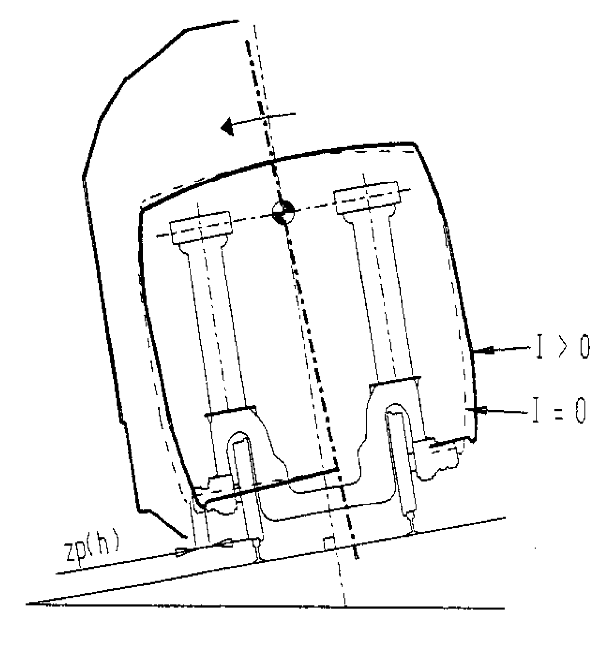
2.4.3.2.2 SITUACIÓN 1. Lado exterior de la curva.
Las figuras 2.23 y 2.24 representan el giro de la caja del vehículo debido a una insuficiencia Ip>Ic>0. (a partir de la posición I=0), en función del sistema de inclinación.
|
SISTEMA ACTIVO La caja gira hacia el exterior de la curva. Los mayores desplazamientos se dan en la parte superior de la caja. |
SISTEMA PASIVO La caja gira hacia el interior de la curva. Los mayores desplazamientos se dan en la parte inferior de la caja. |
|

|
|
Nota: No se representa la inclinación impuesta por el sistema. Figura 2.23. |
Figura 2.24. |
|
Considerando el contorno de referencia del lado exterior de la curva, los puntos del vehículo situados a una altura h>hc se aproximan al mismo, es decir, el desplazamiento ztotal >0. Lo contrario ocurre en los puntos situados a una altura h<hc. Para una insuficiencia de peralte Ip>Ic, los desplazamientos cuasiestáticos serán:
|
Considerando el contorno de referencia del lado exterior de la curva, los puntos del vehículo situados a una altura h>hc se alejan del mismo, es decir, el desplazamiento ztotal <0. Lo contrario ocurre en los puntos situados a una altura h<hc. Para una insuficiencia de peralte Ip>Ic, los desplazamientos cuasiestáticos serán:
|
2.4.3.2.3 SITUACIÓN 2. Lados interior y exterior de la curva.
Los desplazamientos cuasiestáticos zp serán los correspondientes a los vehículos clásicos definidos en el apartado 2.3, es decir:
![]()
2.4.3.3 Valores Ic e Ip
El operador con los datos que le facilite el administrador de la infraestructura deberá asegurar que, en cualquier situación operativa, se cumple la limitación 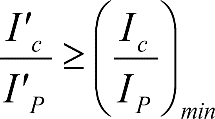 , para los valores de
, para los valores de ![]() indicados en el cuadro 2.6.
indicados en el cuadro 2.6.
En función del ancho de vía se adoptarán para el cálculo de los desplazamientos cuasiestáticos los valores de Ic y máximo de Ip indicados en el cuadro 2.6.
| Ancho de vía | 1668 | 1435 |
|---|---|---|
|
|
175/1,0 | 153/1,0 |
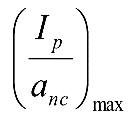
|
318/1,8 | 275/1,8 |
|
|
0,56 | 0,56 |
|
Cuadro 2.6. Valores de Ic y máximo de Ip |
||
2.4.3.4 Fórmulas de reducción
Son las definidas en los apartados 2.7 y 2.8, sustituyendo z por el valor de zp definido en el apartado 2.4.3.2, y con las particularidades indicadas en los apartados 2.4.3.4.1 y 2.4.3.4.2.
2.4.3.4.1 Sistema activo
a) Para la situación 1 se introducirá en las fórmulas de reducción un término complementario z* que representa la inclinación de la caja impuesta por el sistema:
∙ Lado interior de la curva (se acerca al contorno): 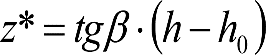
∙ Lado exterior de la curva (se aleja del contorno): 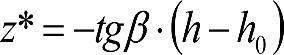
b) Para la validez de las fórmulas, es necesario que la caja se incline proporcionalmente a la insuficiencia de peralte. En los sistemas pasivos esta condición se cumple siempre, ya que la inclinación es provocada por la insuficiencia de peralte. En los sistemas activos, la inclinación de las cajas se fijará externamente durante la concepción o regulación del sistema, por lo que éste deberá garantizar el cumplimiento de las condiciones siguientes:
– Los valores intermedios de I’p, I’c y D’ comprendidos entre 0 y sus valores máximos, deben verificar que:
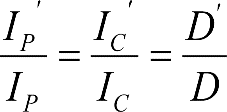
– En el caso de verificación de vehículos en el lado exterior de la curva, el giro de la caja impuesto por el sistema (hacia el interior de la curva) deberá compensar, e incluso superar, al giro cuasiestático de la caja (hacia el exterior de la curva) debido a la fuerza centrífuga, es decir:
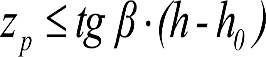
siendo:
β: giro de la caja impuesto por el sistema.
c) Para los distintos valores de Ip, Ic y β, el constructor del VCI calculará las reducciones necesarias. Al final deberá encontrar la combinación de valores (Ip,Ic) que den el valor máximo de zp, y en consecuencia, la máxima reducción.
A tal efecto deberá tener en cuenta las posiciones de los mayores salientes permitidos para las cajas en las diferentes secciones de vía (rectas, transiciones y curvas) y las tolerancias posibles respecto a la posición efectiva del vehículo (debido a retardos del accionamiento del sistema, inercias, rozamientos, etc.).
d) Considerando la previsible evolución técnica de los VCI, en el futuro se podrán añadir hipótesis y modificaciones a las fórmulas propuestas.
Terminado el estudio de todas las situaciones operativas a verificar, el constructor del VCI realizará una comparación de los diferentes semianchos admisibles y elegirá, para cada altura h considerada, el valor más pequeño.
2.4.3.4.2 Sistema pasivo. Vehículos tipo TALGO
En el caso de vehículos tipo TALGO, con ruedas independientes, se utilizarán las siguientes fórmulas de reducción:
a) Situación 1:
∙ Secciones internas: 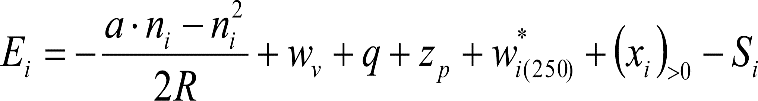

∙ Secciones externas: 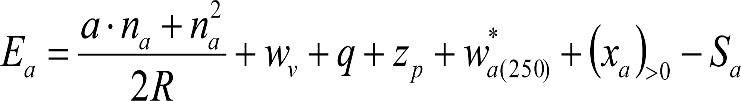
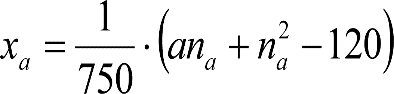
b) Situación 2:
∙ Secciones internas: 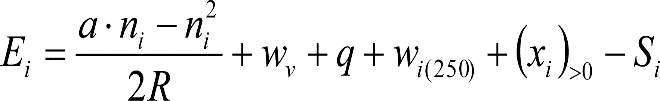
2.4.4 CONDICIONES SOBRE LA VELOCIDAD DE LOS VCI
Para los VCI se puede definir una velocidad máxima de circulación, superior a la máxima en la sección de vía considerada y función de ésta.
La insuficiencia de peralte está ligada a la velocidad mediante la fórmula:
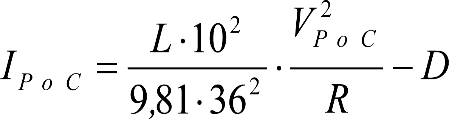
siendo:
Vp: velocidad admitida para los VCI, en km/h.
Vc: velocidad máxima para la sección de vía considerada, según el régimen de velocidad de la línea, en km/h.
R: radio de la curva, en metros.
de donde se obtiene que la velocidad máxima admitida para los VCI será:
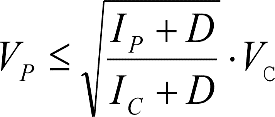
2.5 CÁLCULO DEL GÁLIBO DEL PANTÓGRAFO EN POSICIÓN DE CAPTACIÓN
2.5.1 PANTÓGRAFOS EN VEHÍCULOS CLÁSICOS
Se comprobará que los desplazamientos laterales máximos del pantógrafo en el vehículo real, no superan a los del vehículo tipo usado para definir los contornos de referencia de los apartados 3.10.4.1, 3.11.4.1 y 3.12.4.1. Es decir, que la diferencia (P) entre las reducciones laterales del contorno de referencia en el vehículo real (E), y las del vehículo tipo (Etipo), serán menor o igual que cero. De este modo el pantógrafo en posición de captación permanecerá dentro del contorno de referencia del pantógrafo.
|
(1) Eje de la vía (2) Contorno de referencia del pantógrafo (3) Desplazamiento del pantógrafo (4) Hilo de contacto Figura 2.25. Gálibo del pantógrafo |
Las reducciones del semiancho del contorno de referencia serán las correspondientes al vehículo (indicadas en el apartado 2.3), más las propias del pantógrafo. Para secciones internas (Ei) y externas (Ea) serán, respectivamente:
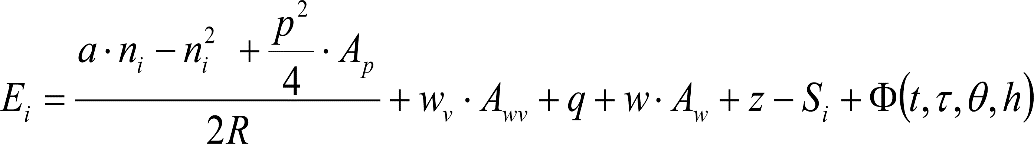
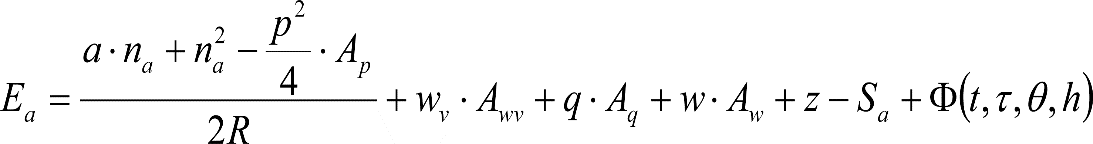
donde:
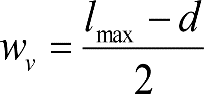
l máx = l N +0,03

t, τ, θ: parámetros de desplazamientos propios del pantógrafo, indicados más abajo.
ht: altura de la articulación más baja del pantógrafo respecto al plano de rodadura.
Las reducciones del semiancho del contorno de referencia en el vehículo real serán:
Para la altura máxima (h’o) de verificación del gálibo:
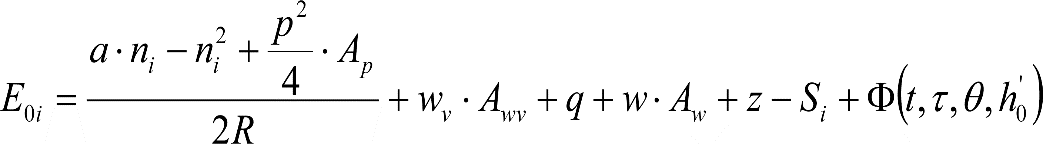

Para la altura mínima (h’u) de verificación del gálibo:

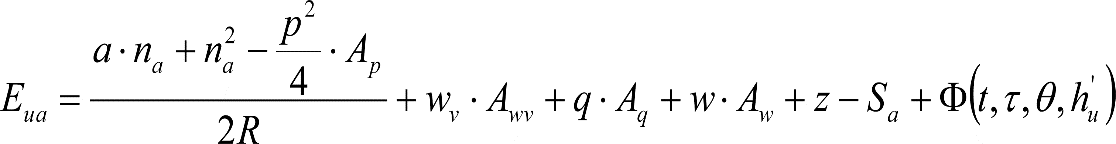
Para calcular z (en ausencia de disimetría) se consideran un exceso y una insuficiencia de peralte, D’o e I’o. Para s > s’o, se deberá corregir el valor de z1, considerando el efecto del exceso (Dmáx-D’o) de peralte y de la insuficiencia (Imáx-I’o) de peralte para la parte de flexibilidad que excede de s’o. Esto se debe a que el exceso (Dmax-D’o) e insuficiencia (Imax-I’o) están considerados en la determinación del gálibo de implantación de obstáculos, pero suponiendo un coeficiente de flexibilidad de los vehículos s’o.

Las características del vehículo tipo son:
∙ Holgura lateral entre eje de ruedas y vía: 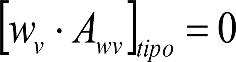
∙ Holguras laterales, q y w: 
∙ Flexibilidad de la suspensión: s ≤ s’o
∙ Índice de flexibilidad del pantógrafo: t = 0,030 m.
∙ Tolerancia de construcción y fijación del pantógrafo: τ = 0,010 m.
∙ Tolerancia de reglaje de la suspensión: θ = 0,005 rad. Este giro produce un desplazamiento adicional del pantógrafo de θ·(h-hc).
Para un vehículo tipo con su eje de ruedas centrado respecto al eje de la vía, los máximos desplazamientos laterales del pantógrafo a ambos lados de dicho eje, para las dos alturas de verificación, serán:
∙ Para la máxima (h’o): 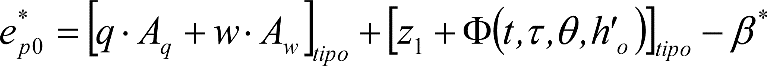
∙ Para la mínima (h’u): 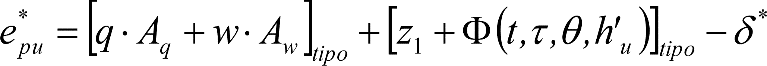
∙ Para una intermedia (h): 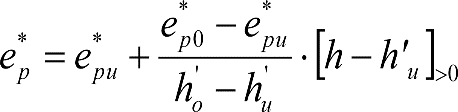
siendo:
β* = 0,005 m, es una reducción para cubrir el carácter aleatorio de los desplazamientos.
δ* = 0,02 m, es una reducción para cubrir el carácter aleatorio de los desplazamientos.
Las reducciones del semiancho del contorno de referencia en el vehículo tipo serán:
Para la altura máxima (h’o) de verificación del gálibo:
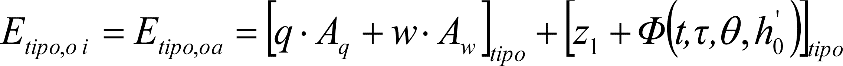
Para la altura mínima (h’u) de verificación del gálibo:

Como se ha dicho antes, la diferencia P entre los desplazamientos laterales del pantógrafo en el vehículo real y en el tipo, deberá cumplir:
∙ En secciones internas: 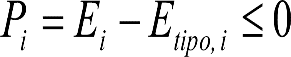
∙ En secciones externas: 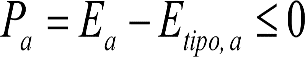
es decir:
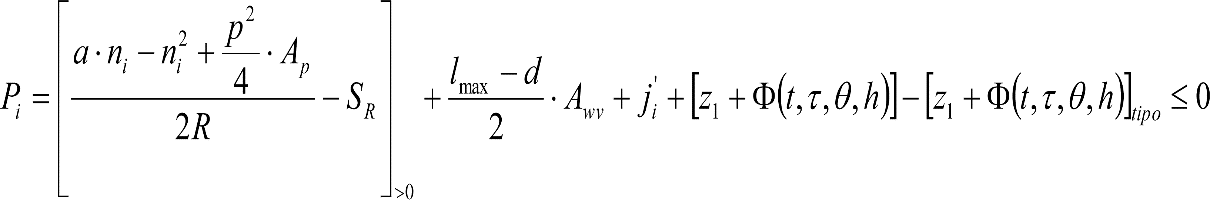
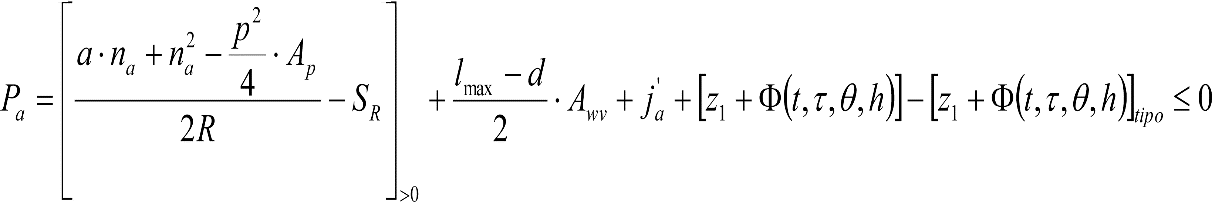
siendo:


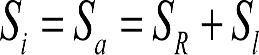
Para la altura máxima (h’o) de verificación del gálibo:
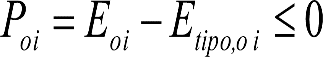

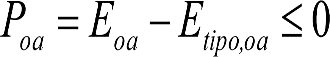
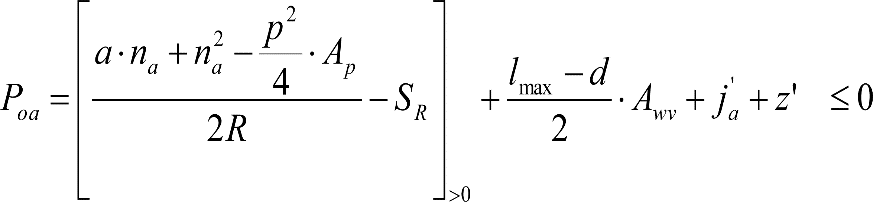
siendo:

Para la altura mínima (h’u) de verificación del gálibo:
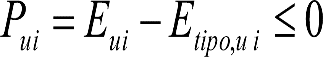
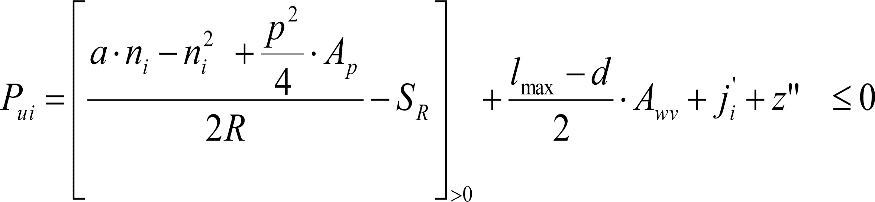

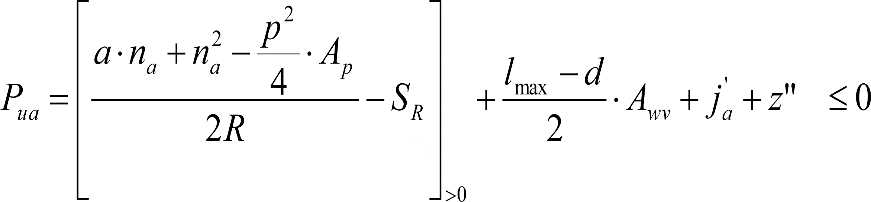
siendo:
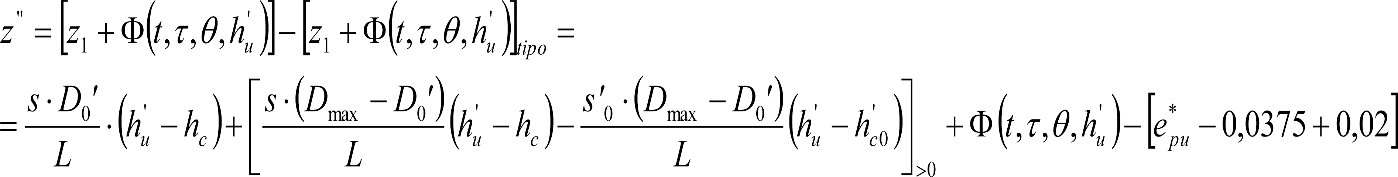
Análogamente se obtendrían los valores de z’ y z’’ para una insuficiencia de peralte Imáx, sustituyendo Dmáx por Imáx, y D’o por I’o.
2.5.1.1 Secciones internas
En el caso de dos bogies motores, en curva: Awv = Aw = Ap = 1.
a) Para s ≤ s’0 y alturas de verificación h’0 y h’u

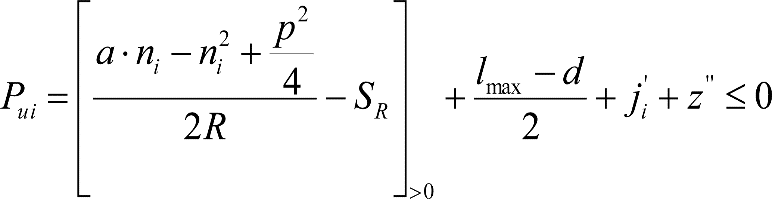
siendo:


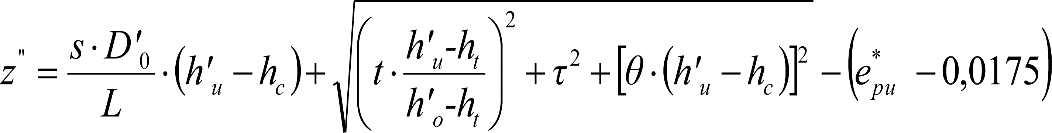
b) Para s > s’0 y alturas de verificación h’0 y h’u


siendo:

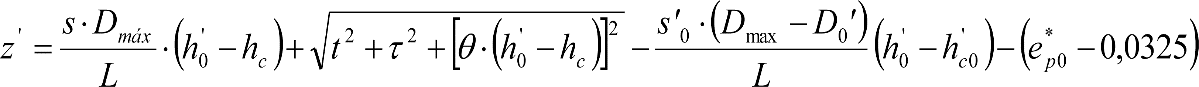
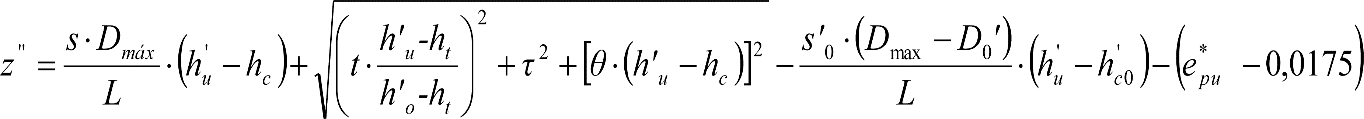
2.5.1.2 Secciones externas
En el caso de dos bogies motores, en curva: 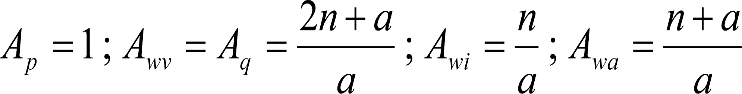
a) Para s ≤ s’0 y alturas de verificación h’0 y h’u

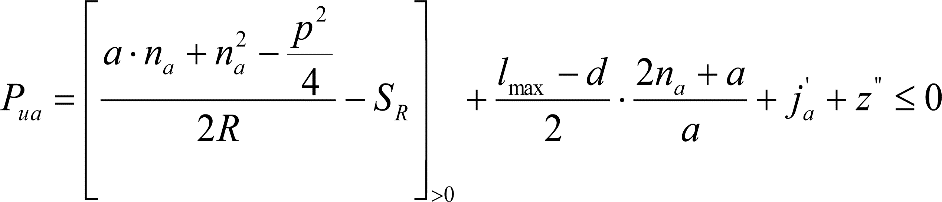
siendo:



b) Para s > s’0 y alturas de verificación h’0 y h’u

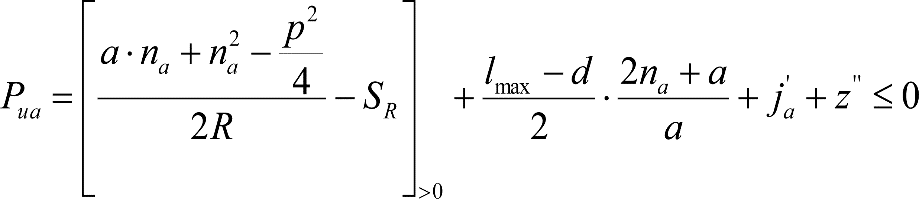
siendo:
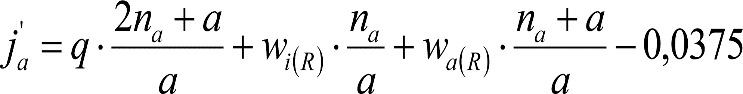
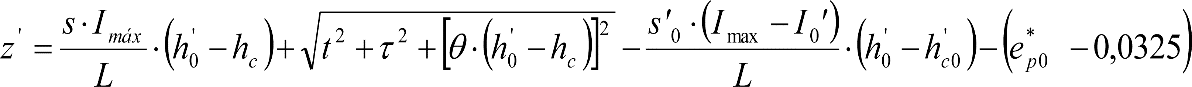

Los valores de z’ y z’’ se definen en los apartados 2.7.5, 2.8.5 y 2.9.4.
2.5.2 PANTÓGRAFOS EN VEHÍCULOS DE CAJA INCLINABLE
En los VCI, el giro de la caja puede crear problemas de contacto entre el pantógrafo y la catenaria, debido a los desplazamientos transversales de aquél. La solución será fijar el pantógrafo a estructuras que no giren, o bien utilizar pantógrafos dotados de sistemas contrarrotación para contrarrestar ésta.
Se considerará lo siguiente:
– En el caso de sistemas contrarrotación, el pantógrafo deberá permanecer en el interior del contorno de referencia del vehículo tipo como en el caso de los vehículos convencionales.
– El constructor del vehículo deberá realizar un análisis de riesgos contemplando los diferentes modos de fallo de los sistemas contrarrotación, a fin de evitar cualquier contacto con la catenaria y principalmente el arranque del hilo de contacto.
2.5.2.1 Pantógrafos independientes del sistema de inclinación de la caja
2.5.2.1.1 Secciones internas
a) Vehículo parado en vía peraltada
Las fórmulas serán análogas a las de los vehículos convencionales.
b) Vehículo circulando en curva con insuficiencia de peralte
Se utilizan las fórmulas generales del apartado 2.5.1.1, sustituyendo:
z1 por z1p
z’ por z’p
z» por z»p
Para sn ≤ s’0 y alturas de verificación h’0 y h’u
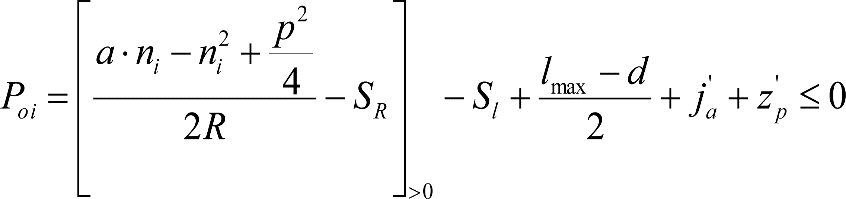
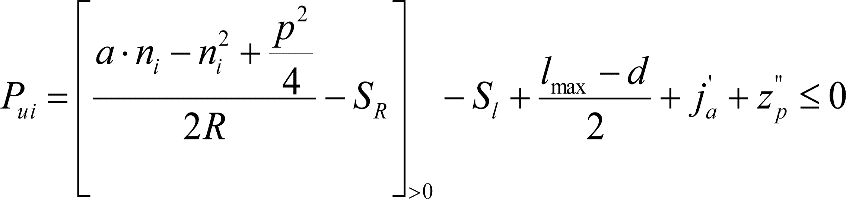
siendo:
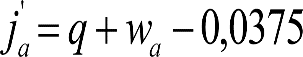
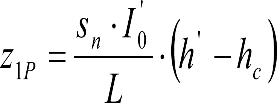

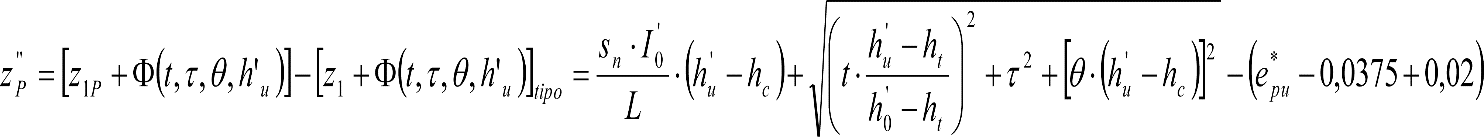
siendo sn el coeficiente de flexibilidad de la estructura portante del pantógrafo.
Para sn> s’0 y alturas de verificación h’0 y h’u
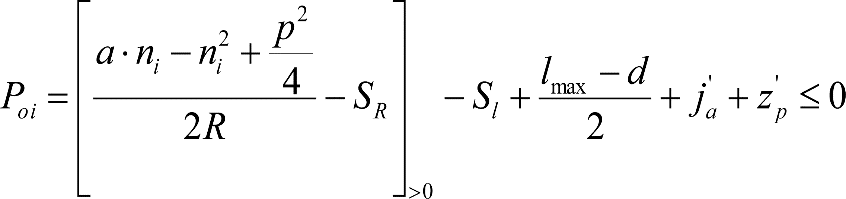

siendo:
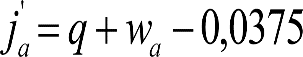
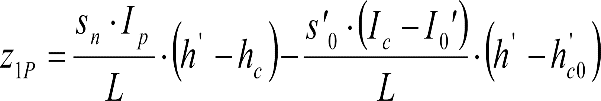
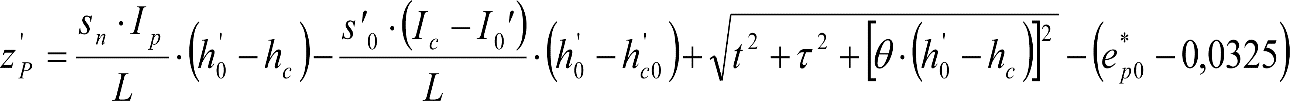
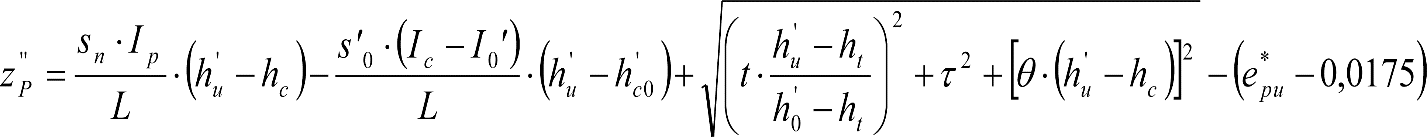
2.5.2.1.2 Secciones externas
Vehículo circulando en curva con insuficiencia de peralte
Se utilizan las fórmulas generales del apartado 2.5.1.2, sustituyendo:
z1 por z1p
z’ por z’p
z» por z»p
Para sn ≤ s’0 y alturas de verificación h’0 y h’u

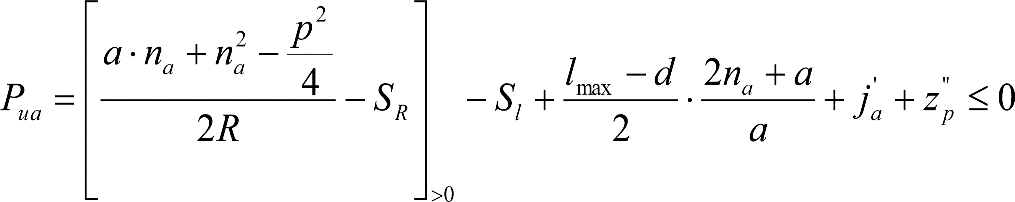
La verificación se realizará con el valor de R que maximiza los valores de Poa y Pua.
siendo:

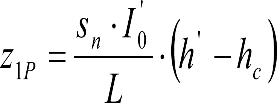

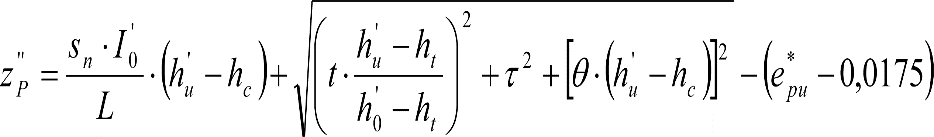
Para sn> s’0 y alturas de verificación h’0 y h’u
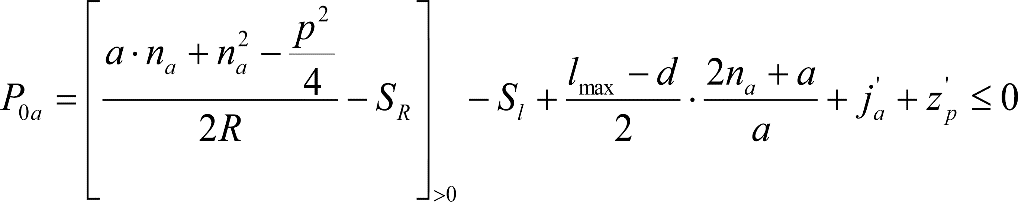
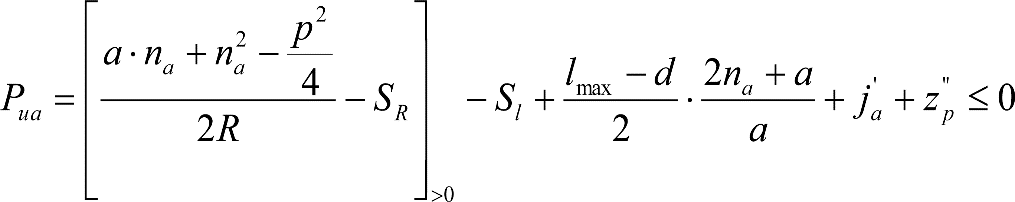
La verificación se realizará con el valor de R que maximiza los valores de Poa y Pua.
siendo:


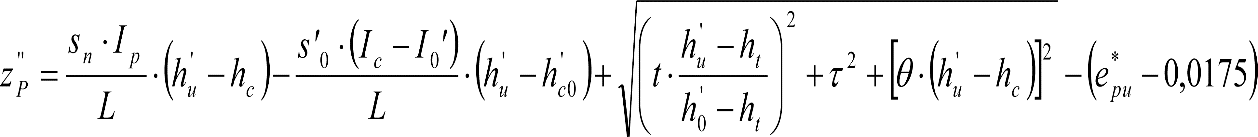
2.5.2.2 Pantógrafos dependientes del sistema de inclinación de la caja.
En este caso, los giros que afectan al pantógrafo se reproducen en la figura 2.26.
|
η: Giro de la caja debido a la flexibilidad de las suspensiones. β’: Giro de la caja del vehículo impuesto por el sistema de inclinación activo. α: Ángulo de contrarrotación del pantógrafo. h0: Altura del centro de rotación de la caja, para el giro impuesto por el sistema. hp: Altura del centro de rotación del pantógrafo. Figura 2.26. Posición de los centros de rotación y ángulos asociados |
El desplazamiento del pantógrafo debido al giro de la caja impuesto por el sistema será:  .
.
El desplazamiento del pantógrafo debido a su contrarrotación será:  .
.
A fin de que los valores Poi, Pui, Poa y Pua sean negativos o nulos, el fabricante del vehículo desplazará el pantógrafo una cantidad al menos igual al valor positivo dado por las fórmulas siguientes.
a) Secciones internas
Para la altura máxima (h’o) de verificación del gálibo:
Cuando:
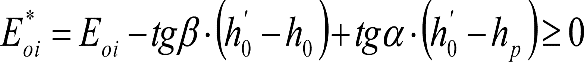

Cuando:
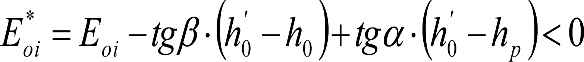
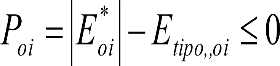
siendo:
E*0i: desplazamiento en secciones internas del vehículo real dotado de pantógrafo dependiente del sistema de inclinación de la caja a la altura máxima de verificación del gálibo (h’0).
E0i: desplazamiento en secciones internas del vehículo real convencional a la altura máxima de verificación del gálibo (h’0), definido en el apartado 2.5.1.
Etipo,0i: desplazamiento del vehículo tipo a la altura máxima de verificación del gálibo (h’0), definido en el apartado 2.5.1.
Para la altura mínima (h’u) de verificación del gálibo:
Cuando:
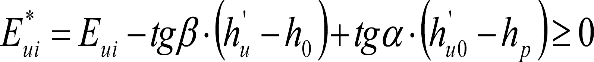
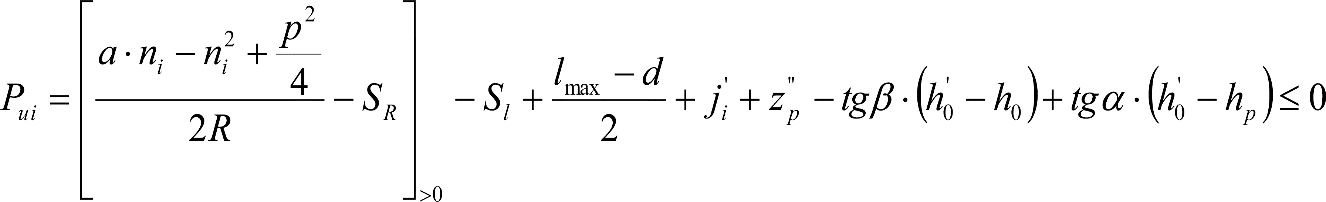
Cuando:
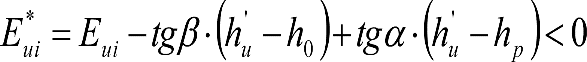
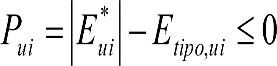
siendo:
E*ui: desplazamiento en secciones internas del vehículo real dotado de pantógrafo dependiente del sistema de inclinación de la caja a la altura mínima de verificación del gálibo (h’u).
Eui: desplazamiento en secciones internas del vehículo real convencional a la altura mínima de verificación del gálibo (h’u), definido en el apartado.
Etipo,ui: desplazamiento del vehículo tipo a la altura mínima de verificación del gálibo (h’u), definido en el apartado 2.5.1.
b) Secciones externas
Para la altura máxima (h’o) de verificación del gálibo:
Cuando:
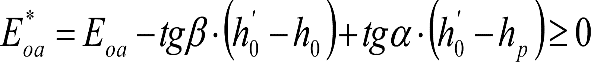

Cuando:


siendo:
E*0a: desplazamiento en secciones externas del vehículo real dotado de pantógrafo dependiente del sistema de inclinación de la caja a la altura máxima de verificación del gálibo (h’0).
E0a: desplazamiento en secciones externas del vehículo real convencional a la altura máxima de verificación del gálibo (h’0), definido en el apartado 2.5.1.
Etipo,0a: desplazamiento del vehículo tipo a la altura máxima de verificación del gálibo (h’0), definido en el apartado 2.5.1.
Para la altura mínima (h’u) de verificación del gálibo:
Cuando:


Cuando:
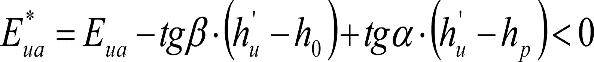
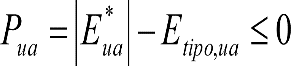
siendo:
E*ua: desplazamiento en secciones externas del vehículo real dotado de pantógrafo dependiente del sistema de inclinación de la caja a la altura mínima de verificación del gálibo (h’u).
Eua: desplazamiento en secciones externas del vehículo real convencional a la altura mínima de verificación del gálibo (h’u), definido en el apartado.
Etipo,ua: desplazamiento del vehículo tipo a la altura mínima de verificación del gálibo (h’u), definido en el apartado 2.5.1.
2.5.3 CONTORNO DE REFERENCIA DE LOS PANTÓGRAFOS Y DE LAS PARTES DEL VEHÍCULO SUSCEPTIBLES DE ESTAR EN TENSIÓN ELÉCTRICA, NO AISLADAS, SITUADAS EN EL TECHO
Se reducirá el contorno de referencia cinemático del material en la distancia de aislamiento, en aquellas partes del vehículo susceptibles de estar en tensión eléctrica situadas en el techo.
Dichas partes en tensión no deberán penetrar en las áreas rayada y sombreada, definidas en la figura 2.27.
En las líneas electrificadas el área sombreada definida en la figura 2.27 podrá ser utilizada por los pantógrafos bajados y por las partes del vehículo que no estén bajo tensión.
En el caso de líneas no electrificadas la utilización de las zonas especiales requerirá llevar a cabo un estudio especial a fin de comprobar la no interferencia con los obstáculos.
2.6 ELEMENTOS RETRÁCTILES EN OPERACIÓN DE APERTURA
En aquellos casos en que no se pueda garantizar que los elementos móviles están cerrados cuando el vehículo está en movimiento se podrán aplicar las siguientes salvedades:
En andenes, con el vehículo en su posición más baja posible, y para velocidades menores o iguales a 5 km/h, los siguientes elementos retráctiles podrán rebasar el gálibo del material rodante, en los valores máximos indicados a continuación.
a) Elementos tales como puertas, espejos, etc, en posición de apertura:
a.1) Para alturas sobre el plano de rodadura superiores a 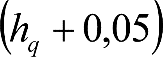 : 0,2 m.
: 0,2 m.
a.2) Para alturas sobre el plano de rodadura menores o iguales a 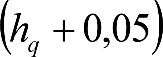 :
:
∙ Secciones internas: wi, con 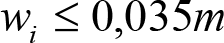 .
.
∙ Secciones externas: 
Se determinará la holgura lateral residual x, que depende de la tecnología del vehículo. A falta de datos, se adoptará un valor de x=0,02 m, puesto que a velocidad del vehículo igual o inferior a 30 km/h los juegos transversales no superan dicho valor.
b) Peldaños en posición de apertura:
∙ Secciones internas: wi, con 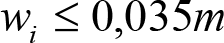 .
.
∙ Secciones externas: 
Asimismo se comprobará que el punto situado en el centro del mamperlán del peldaño de cada puerta de acceso a ambos lados de un vehículo colocado centralmente en el carril y en condiciones de servicio, con ruedas nuevas pero sin viajeros, se encuentra en el área de situación del peldaño de la figura 2.28, para cada tipo de andén utilizado por el material rodante, en condiciones normales de explotación.
La comprobación se realizará, tanto para vehículo situado en alineación recta, como en curva de radio 300 m (ancho ibérico y estándar europeo), o 100 m (ancho métrico).
|
(*) Desplazamiento admitido del pantógrafo. Permite verificar que el desplazamiento no sobrepasa el valor máximo admitido por la infraestructura (1) Altura máxima del pantógrafo bajado (2) Contorno de referencia cinemático (3) Plano de rodadura (4) Altura del contorno de referencia cinemático (5) Distancia de aislamiento eléctrico según la UNE-EN 50119:2.010
Figura 2.27. Contorno de referencia de los pantógrafos y de las partes del vehículo susceptibles de estar en tensión eléctrica, no aisladas, situadas en el techo |
|
δv+: Máxima diferencia de altura entre el peldaño y el andén (peldaño por encima del andén). δv-: Máxima diferencia de altura entre el peldaño y el andén (peldaño por debajo del andén). δh: Distancia que determina la zona a la que puede ubicarse el umbral del peldaño respecto bqo. bqo: Máxima distancia entre el umbral del peldaño y el eje de la vía. Los valores de δv+,δv-,δhy bqo se indican en los apartados 2.7.6 y 2.8.6 en función del ancho de vía. Figura 2.28. Situación del peldaño |
2.7 APLICACIÓN A LÍNEAS CON ANCHO IBÉRICO
2.7.1 CONTORNOS DE REFERENCIA
Se consideran los siguientes contornos de referencia en las partes altas:
∙ GHE16
∙ GEA16
∙ GEB16
∙ GEC16
Se consideran los siguientes contornos de referencia en las partes bajas:
∙ GEI1: material rodante apto para circular por vías equipadas con frenos de vía en posición activa y lomos de asno de las estaciones de clasificación.
∙ GEI2: material rodante no apto para circular por vías equipadas con frenos de vía en posición activa ni lomos de asno de las estaciones de clasificación.
Los vehículos motores de maniobras utilizados en las estaciones de clasificación podrán tener el gálibo GEI2 si van a pasar por los lomos de asno con los frenos de vía en posición no activa.
∙ GEI3: material rodante apto para circular por vías acondicionadas para transporte mediante autopista ferroviaria.
2.7.1.1 Contornos de referencia de las partes altas
2.7.1.1.1 GHE16
El contorno de referencia de las partes altas se define en la figura 2.29.
|
(1) Plano de rodadura NOTA Partes bajas definidas en las figuras 2.33, 2.34 y 2.35 Figura 2.29. Contorno de referencia del gálibo cinemático GHE16. Partes altas |
2.7.1.1.2 GEA16
Este contorno es una envolvente de los contornos GHE16 y GA (definido en la norma EN15273-2:2.013).
La figura 2.30 define el contorno de referencia para las partes altas.
|
(1) Plano de rodadura NOTA Partes bajas definidas en las figuras 2.33, 2.34 y 2.35 Figura 2.30. Contorno de referencia del gálibo cinemático GEA16. Partes altas |
2.7.1.1.3 GEB16
Este contorno es una envolvente de los contornos GHE16 y GB (definido en la norma EN15273-2:2.013).
La figura 2.31 define el contorno de referencia para las partes altas.
|
(1) Plano de rodadura NOTA Partes bajas definidas en las figuras 2.33, 2.34 y 2.35 Figura 2.31. Contorno de referencia del gálibo cinemático GEB16. Partes altas |
2.7.1.1.4 GEC16
Este contorno es una envolvente de los contornos GHE16 y GC (definido en la norma EN15273-2:2.013).
La figura 2.32 define el contorno de referencia para las partes altas.
|
(1) Plano de rodadura NOTA Partes bajas definidas en las figuras 2.33, 2.34 y 2.35 Figura 2.32. Contorno de referencia del gálibo cinemático GEC16. Partes altas |
2.7.1.2 Contornos de referencia de las partes bajas
2.7.1.2.1 GEI1
La figura 2.33 define el contorno de referencia del gálibo cinemático GEI1.
|
(1) Plano de rodadura l: Ancho de vía Figura 2.33. Contorno de referencia del gálibo cinemático GEI1. Partes bajas |
2.7.1.2.2 GEI2
La figura 2.34 define el contorno de referencia del gálibo cinemático GEI2.
|
(1) Plano de rodadura l: Ancho de vía Figura 2.34. Contorno de referencia del gálibo cinemático GEI2. Partes bajas |
2.7.1.2.3 GEI3
La figura 2.35 define el contorno de referencia del gálibo cinemático GEI3, en el caso de que el material rodante sea apto para circular por vías acondicionadas para transporte mediante autopista ferroviaria. Este contorno es una envolvente de los contornos GHE16 y GI3 (definido en la norma EN 15273-2:2013).
|
(1) Plano de rodadura l: Ancho de vía Figura 2.35. Contorno de referencia del gálibo cinemático GEI3 del material apto para circular por autopista ferroviaria. Partes bajas |
2.7.2 REGLAS ASOCIADAS
2.7.2.1 desplazamientos verticales
Serán los indicados en el apartado 2.2.2, con las particularidades siguientes:
1) Los desplazamientos verticales a considerar en la determinación de la altura mínima sobre el plano de rodadura, solo se aplicarán a las partes bajas del vehículo situadas a una altura h ≤ 1.150 mm.
2) Los desplazamientos verticales a considerar en la determinación de la altura máxima sobre el plano de rodadura solo se aplicarán a las partes altas del vehículo situadas a una altura h ≥ 3.320 mm.
2.7.2.2 holgura lateral entre eje de ruedas y vía
De la expresión del apartado 2.2.3.2.1, se tiene:
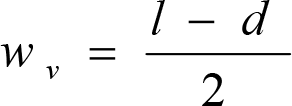
siendo:
l: ancho de vía. Se toma:
l = lmáx = lN + sobre ancho máximo = lN +0,03 = 1,698m (caso general).
l = lN = 1,668m (casos de secciones internas en curva, tanto para vehículos remolcados con dos bogies portadores o cuasiportadores, como para vagones con bogies).
2.7.2.3 desplazamientos por exceso o insuficiencia de peralte y disimetría
Se obtendrán particularizando las fórmulas de los apartados 2.2.3.3 y 2.2.3.4 para los valores siguientes:
hco = 0,5 m
L = 1,733 m
Io = Do = 0,050 m
Dmax= Imax= 0,160 m
a) Vehículos en general

donde:
![]() es valor absoluto, es decir, que si h<hc se toma hc-h.
es valor absoluto, es decir, que si h<hc se toma hc-h.
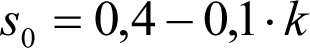 , donde k se define en el cuadro 2.9 en función del gálibo.
, donde k se define en el cuadro 2.9 en función del gálibo.
Finalmente:
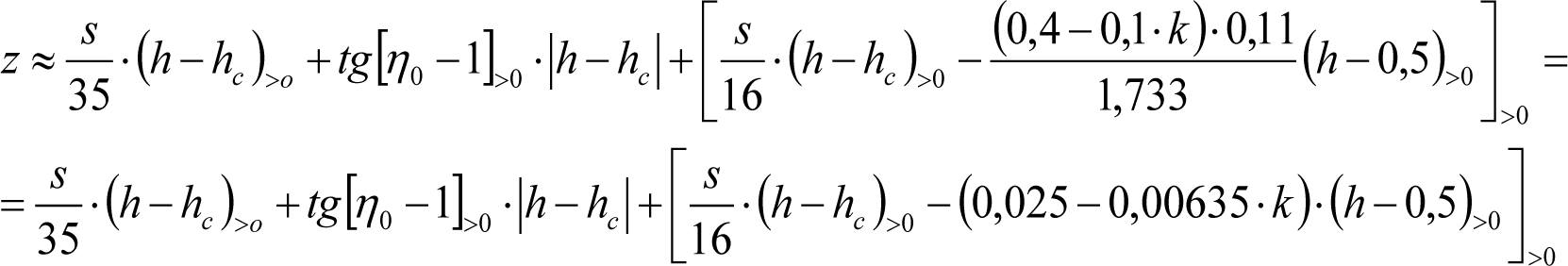
b) Vagones equipados con bogies
∙ Si J ≤ 5 mm: 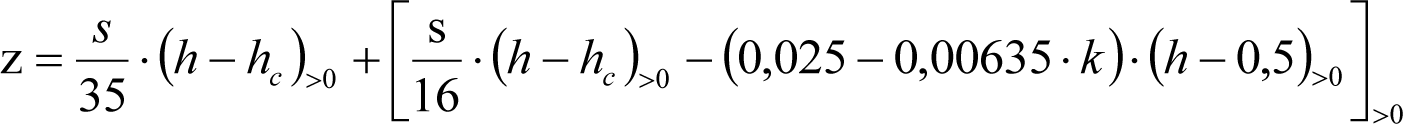
∙ Si J > 5 mm:
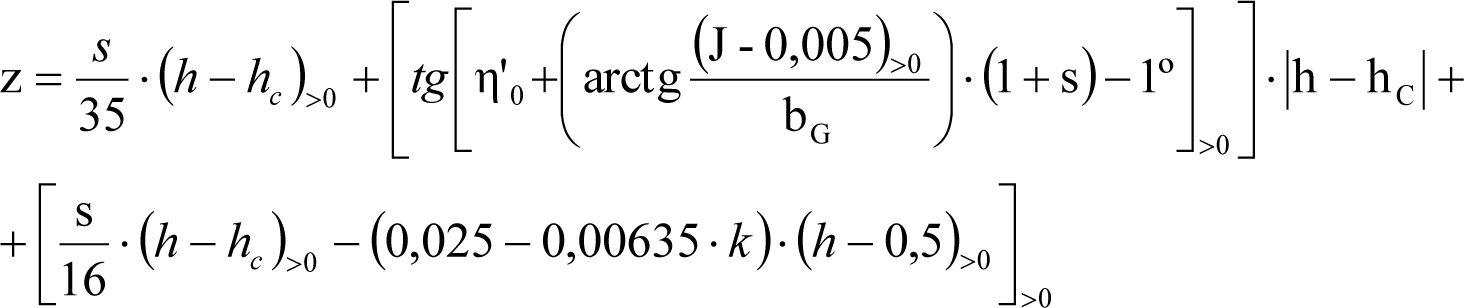
2.7.2.4 Salientes
Se adoptarán los salientes indicados en los cuadros 2.7 y 2.8 en función del gálibo en partes altas y bajas.
Como valor de l se tomará el indicado en el apartado 2.7.2.2.
Como valor de k se tomará el indicado en el cuadro 2.9 en función del gálibo.
| Salientes máximos para un ancho de vía l y para una altura h del punto considerado sobre el plano de rodadura | ||||
|---|---|---|---|---|
| Gálibo | Radio | h > 0,4 m | Zona de pantógrafos | |
| 0,4 m < h ≤ 3,32 m | h > 3,32 m | |||
|
GHE16 GEC16 |
250 ≤ R ≤ ∞ |
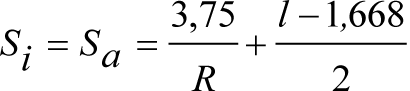
|

|
|
| 150 ≤ R < 250 |
|
|||
|
GEA16 GEB16 |
250 ≤ R ≤ ∞ |
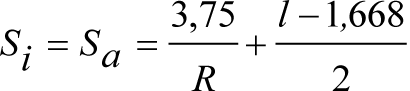
|
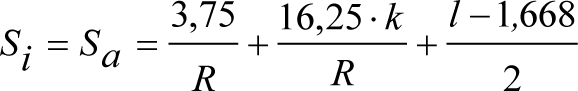
|
|
| 150 ≤ R < 250 |
|
|
||
|
NOTA: Si = Lado interior de la curva (m); Sa = Lado exterior de la curva (m) |
||||
|
Cuadro 2.7. Salientes de los gálibos GHE16, GEA16, GEB16 y GEC16. Partes altas |
||||
| Salientes máximos para un ancho de vía l y para una altura h del punto considerado sobre el plano de rodadura | ||
|---|---|---|
| Gálibo | Radio | h ≤ 0,4 m |
|
GEI1 GEI2 |
250 ≤ R ≤ ∞ |

|
| 150 ≤ R < 250 |
|
|
| GEI3 | 250 ≤ R ≤ ∞ |
|
| 150 ≤ R < 250 |
|
|
|
NOTA: Si = Lado interior de la curva (m); Sa = Lado exterior de la curva (m) |
||
|
Cuadro 2.8. Salientes de los gálibos GEI1, GEI2 y GEI3. Partes bajas |
||
| GÁLIBO | Altura h (m) | s 0 | k |
|---|---|---|---|
| GHE16 | Cualquier altura | 0,4 | 0 |
| GEC16 | Cualquier altura | 0,4 | 0 |
| GEA16 | h ≤ 3,32 | 0,4 | 0 |
| 3,32 < h < 3,70 |
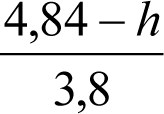
|

|
|
| h ≥ 3,70 | 0,3 | 1 | |
| GEB16 | h ≤ 3,32 | 0,4 | 0 |
| 3,32 < h < 4,11 |
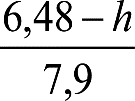
|
|
|
| h ≥ 4,11 | 0,3 | 1 | |
| GEI1 | Cualquier altura | 0,4 | 0 |
| GEI2 | Cualquier altura | 0,4 | 0 |
| GEI3 | h ≤ 0,25 | 0,4 | 1 |
| 0,25 < h ≤ 0,4 | 0,4 |
|
|
|
Cuadro 2.9. Valores de so y k para los gálibos GHE16, GEA16, GEB16, GEC16, GEI1, GEI2 y GEI3 |
|||
2.7.3 CÁLCULO DEL GÁLIBO DEL MATERIAL
2.7.3.1 Fórmulas de reducción para los gálibos GHE16 y GEC16, con gálibo de partes bajas GEI1 y GEI2
2.7.3.1.1 Material motor
Se consideran dos bogies motores.
a) Caso general. Reducción en secciones internas Ei
Para cada punto del vehículo el valor de la reducción Ei que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.

o bien, considerando los distintos salientes Si para partes altas y bajas:
| Para recta R = ∞: | ||||

|
||||
| Para curva de radio R ≥ 250 m: | ||||
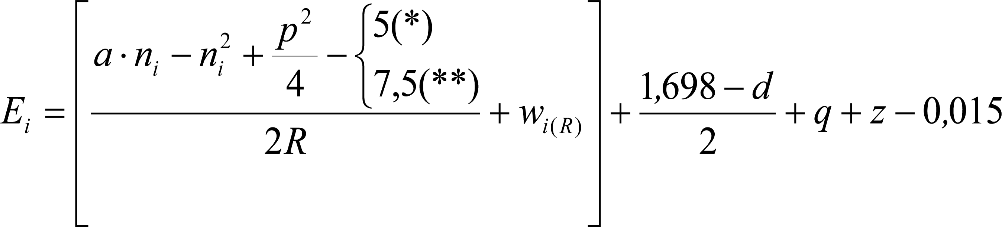
|
||||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |||
| Para curva de radio 150 ≤ R < 250 m: | ||||

|
||||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |||
b) Caso general. Reducción en secciones externas Ea
Para cada punto del vehículo el valor de la reducción Ea que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.

o bien, considerando los distintos salientes Sa para partes altas y bajas:
| Para recta R = ∞: | |||

|
|||
| Para curva de radio R ≥ 250 m: | |||
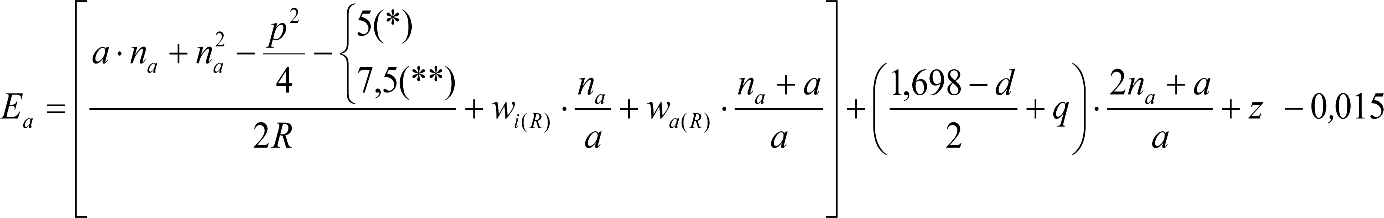
|
|||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | ||
| Para curva de radio 150 ≤ R < 250 m: | |||
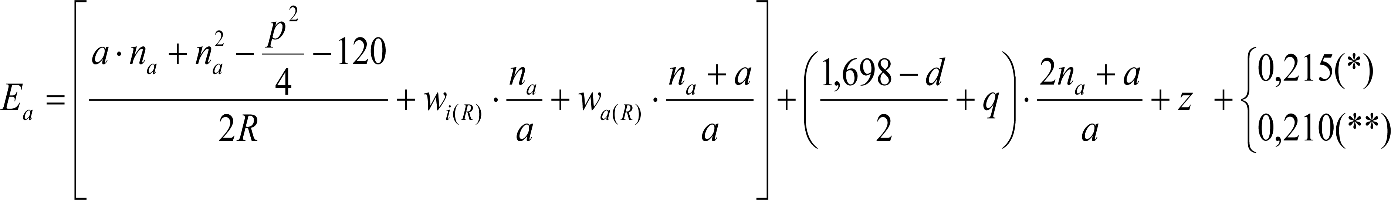
|
|||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | ||
c) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones internas Ei
En este caso: 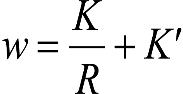 . Las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=250 ó 150 m).
. Las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=250 ó 150 m).
Si: 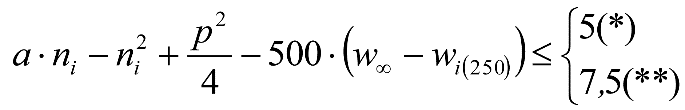 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||||
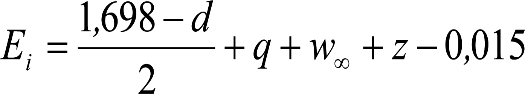
|
||||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |||
Si: 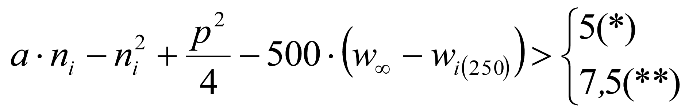 ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |
||||
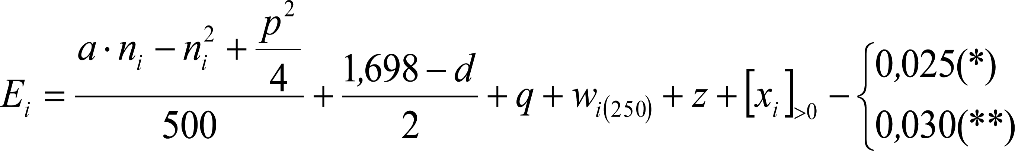
|
||||
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
||||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |||
|
d) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones externas Ea Si: |
||||
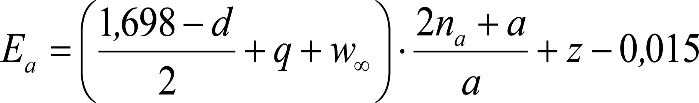
|
||||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | |||
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |
||||
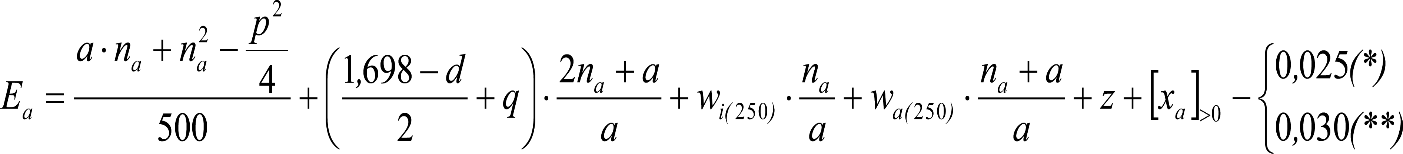
|
||||
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
||||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | |||
2.7.3.1.2 Material remolcado montado sobre bogies
Se consideran indistintamente dos bogies portadores o cuasiportadores.
a) Caso general. Reducción en secciones internas Ei
Para cada punto del vehículo el valor de la reducción Ei que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.
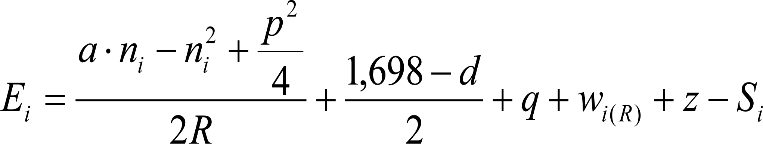
o bien, considerando los distintos salientes Si para partes altas y bajas:
| Para recta R = ∞: | ||||
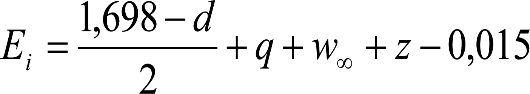
|
||||
| Para curva de radio R ≥ 250 m: | ||||
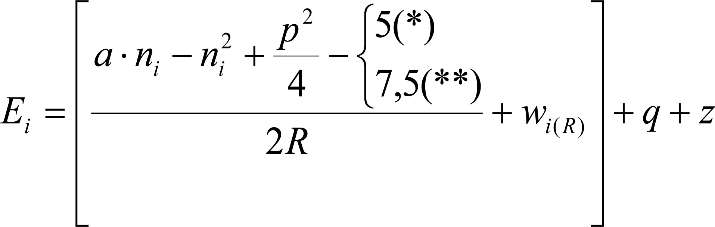
|
||||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |||
| Para curva de radio 150 ≤ R < 250 m: | ||||
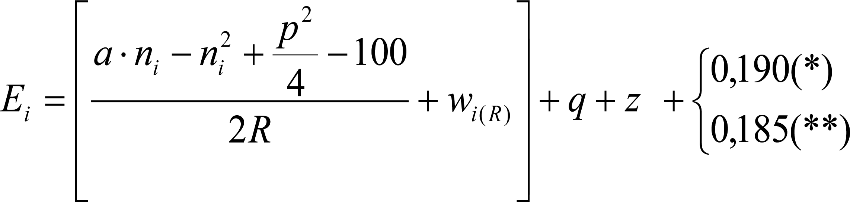
|
||||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |||
b) Caso general. Reducción en secciones externas Ea
Para cada punto del vehículo el valor de la reducción Ea que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.
La reducción considerando los distintos salientes Sa para partes altas y bajas será:
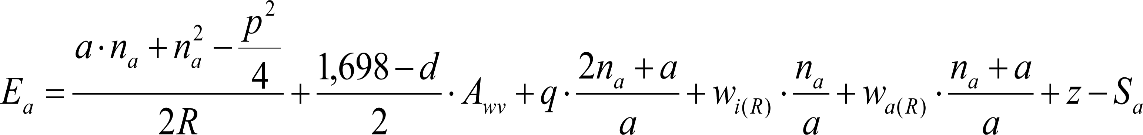
| Para recta R = ∞: | |||

|
|||
| Para curva de radio R ≥ 250 m: | |||
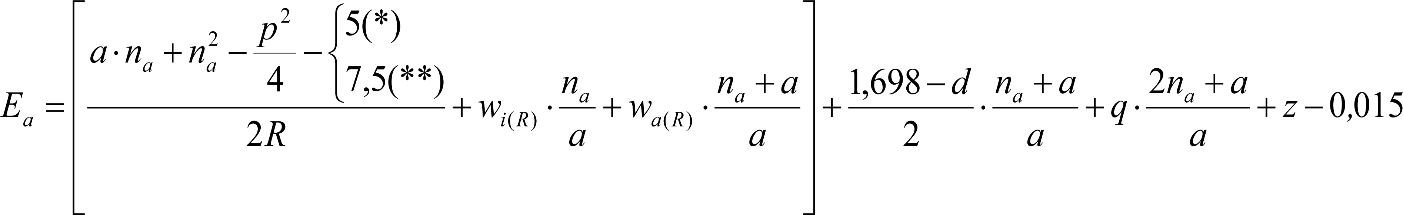
|
|||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | ||
| Para curva de radio 150 ≤ R < 250 m: | |||
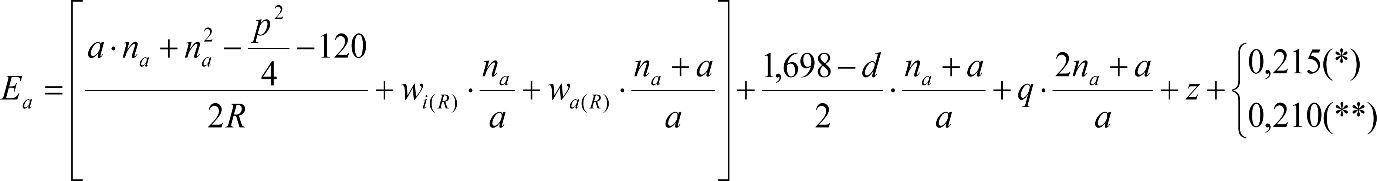
|
|||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | ||
c) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones internas Ei
En este caso: 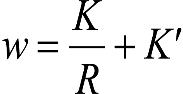 , y las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=250 o 150 m).
, y las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=250 o 150 m).
Si: 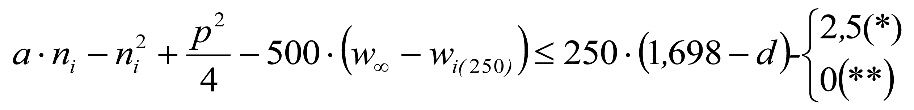 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||
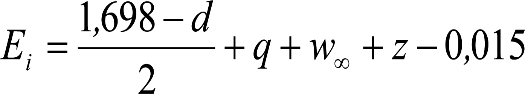
|
||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |
Si: 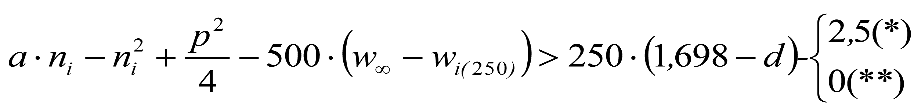 ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |
||
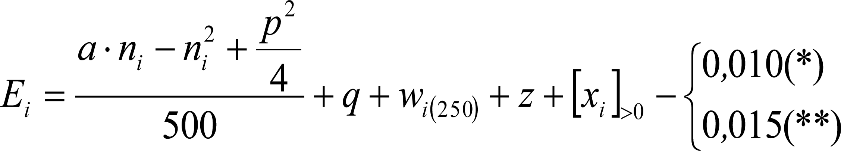
|
||
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |
d) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones externas Ea
Si: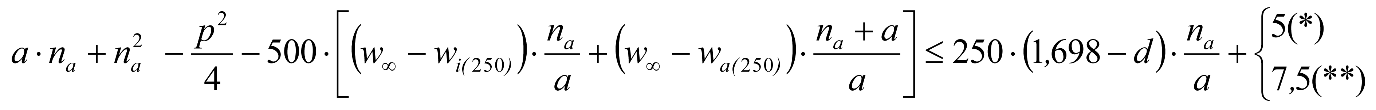 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||
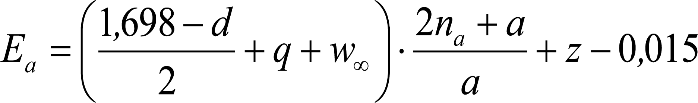
|
||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | |
Si: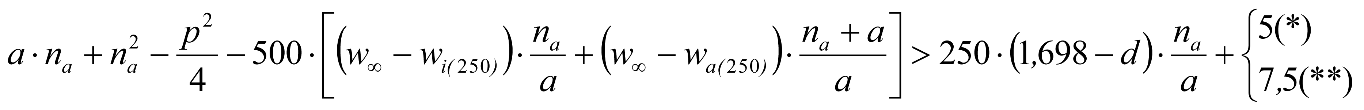 ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |
||
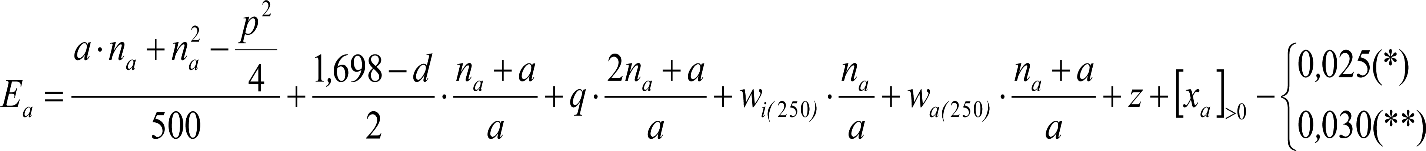
|
||
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | |
e) Caso particular de vagones con bogies. Secciones internas Ei
En este caso, la holgura es constante, es decir, w∞= wi(R)= wa(R) = w.
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||

|
||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |
||
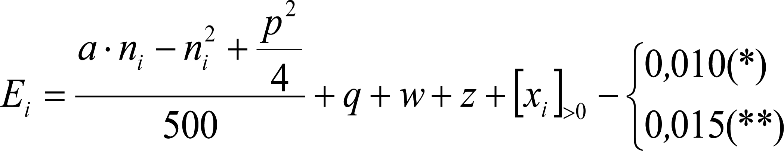
|
||
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |
f) Caso particular de vagones con bogies. Secciones externas Ea
Si: ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||

|
||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | |
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |
||
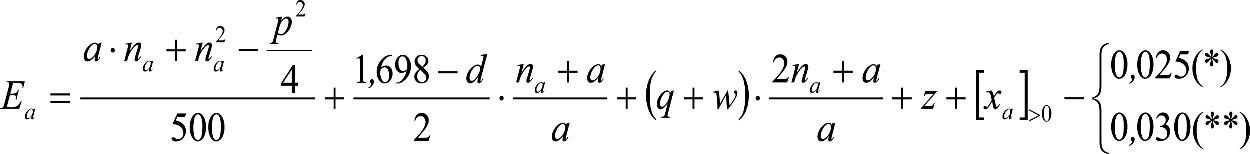
|
||
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | |
2.7.3.1.3 Vagones sin bogies
Las reducciones se obtendrán particularizando las de material motor, con p=0 y w∞= wi(R)= wa(R) = w= 0 (al no existir bogies).
a) Reducción en secciones internas Ei
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
|||
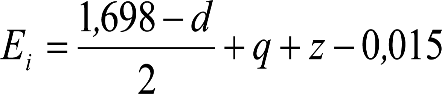
|
|||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | ||
Si: 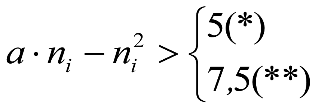 ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |
|||
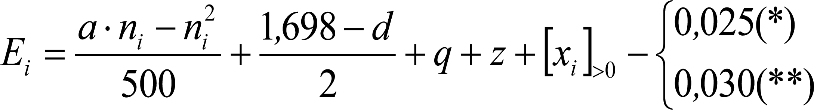
|
|||
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
|||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | ||
b) Reducción en secciones externas Ea
Si: 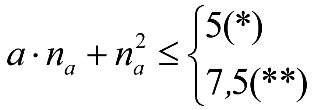 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
|
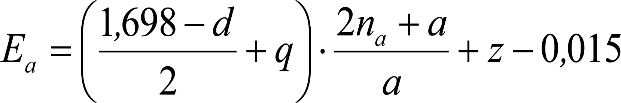
|
|
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) |
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |
|

|
|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
|
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) |
2.7.3.1.4 Vehículos autopropulsados
Se utilizarán las fórmulas de reducción del cuadro 2.10, en función del coeficiente de adherencia rueda-carril (μ).
| Tipo de bogies | Valor de μ de cada bogie | Posición de rodadura sobre la vía | Fórmulas de reducción definidas en apartado |
|---|---|---|---|
| Dos bogies motores | μ ≥ 0,2 | Casos 2 y 5 del cuadro 2.4 | 2.7.3.1.1 |
| Dos bogies cuasi-portadores | 0 <μ < 0,2 | Casos 2 y 7 del cuadro 2.4 | 2.7.3.1.2 |
| Un bogie cuasi-portador y otro portador |
0 <μ < 0,2 μ = 0,2 |
||
| Dos bogies portadores | μ = 0,2 | ||
| Un bogie motor y otro portador |
μ ≥ 0,2 μ = 0,2 |
Casos 3 y 6 del cuadro 2.4 |
2.7.3.1.41 2.7.3.1.11 |
| Un bogie motor y otro cuasi-portador |
μ ≥ 0,2 0 <μ < 0,2 |
||
| Los valores obtenidos de las fórmulas de reducción para vehículos motores y autopropulsados son parecidos. En general se utilizan las de vehículos motores, reservando las fórmulas de autopropulsados para aquellos casos en que la menor reducción obtenida sea significativa (0 a 12,5 mm según la sección considerada del vehículo), lo cual ocurre en el centro y extremos de la caja. | |||
|
Cuadro 2.10. Fórmulas de reducción aplicables a los vehículos autopropulsados |
|||
La potencia de los vehículos autopropulsados es generalmente inferior a la de las locomotoras. Al existir un bogie motor y otro portador, sus características serán diferentes.
Se denomina:
p, w∞, wi(R), wa(R): empate y holguras del bogie motor.
p’, w’∞, w’i(R), w’a(R): empate y holguras del bogie portador.
nμ: distancia desde la sección interior considerada, hasta el pivote del bogie motor.
a) Reducción en secciones internas Ei
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
a.1) En recta:
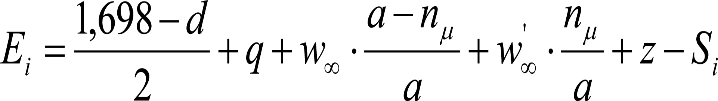
o bien, considerando el saliente Si:

a.2) En curva:
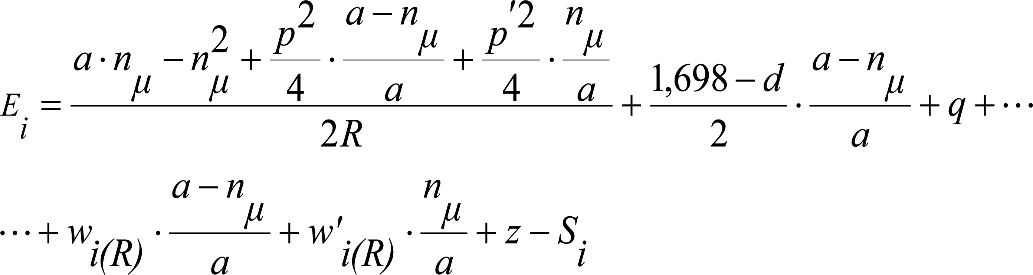
o bien, considerando los distintos salientes Si:
| Para curvas de radio R=250 ó 150 m: | |

|
|
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
|
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
b) Reducción en secciones externas lado bogie motor Ea
En este caso el bogie motor va delante del bogie portador en el sentido de la marcha.
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
b.1) En recta:

o bien, considerando el saliente Sa:
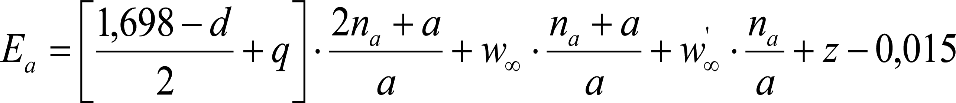
b.2) En curva:

o bien, considerando los distintos salientes Sa:
| Para curvas de radio R=250 ó 150 m: | |
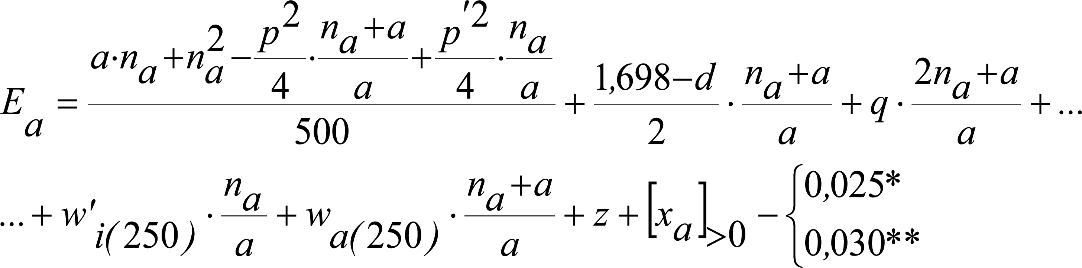
|
|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
|
| (*) valor a aplicar en Ea de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en Ea de partes altas (h > 0,400 m) |
c) Reducción en secciones externas lado bogie portador Ea
En este caso el bogie portador va delante del bogie motor en el sentido de la marcha.
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
c.1) En recta:
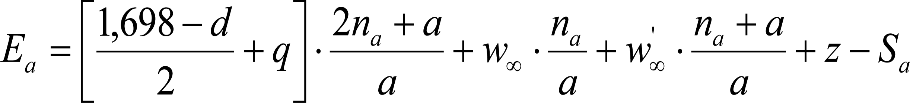
o bien, considerando el saliente Sa:
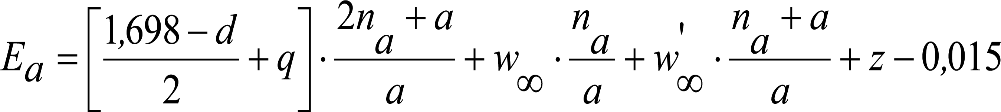
c.2) En curva:
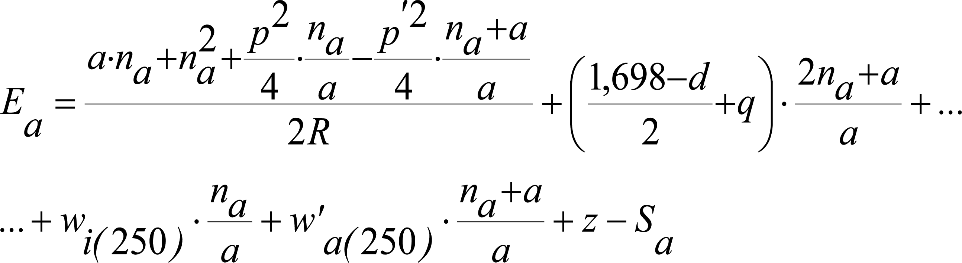
o bien, considerando los distintos salientes Sa:
| Para curvas de radio R=250 ó 150: | |

|
|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
|
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) |
2.7.3.2 Fórmulas de reducción para los gálibos GHE16 y GEC16, con gálibo de partes bajas GEI3
Para h ≥ 0,4 m se aplicarán las fórmulas del apartado 2.7.3.1.
Para h ≤ 0,25 m se aplicarán las fórmulas indicadas a continuación.
Para 0,25 < h < 0,4 m se realizará una interpolación entre los valores obtenidos para h=0,25 m y h=0,4 m.
2.7.3.2.1 Material motor
Se consideran dos bogies motores.
a) Caso general. Reducción en secciones internas Ei
Para cada punto del vehículo el valor de la reducción Ei que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.

o bien, considerando los distintos salientes Si para partes altas y bajas:
| Para recta R = ∞: |

|
| Para curva de radio R ≥ 250 m: |

|
| Para curva de radio 150 ≤ R < 250 m: |
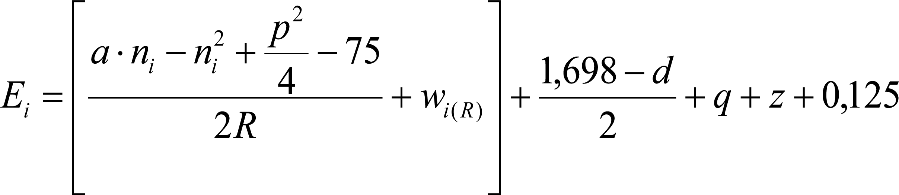
|
b) Caso general. Reducción en secciones externas Ea
Para cada punto del vehículo el valor de la reducción Ea que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.

o bien, considerando los distintos salientes Sa para partes altas y bajas:
| Para recta R = ∞: |

|
| Para curva de radio R ≥ 250 m: |
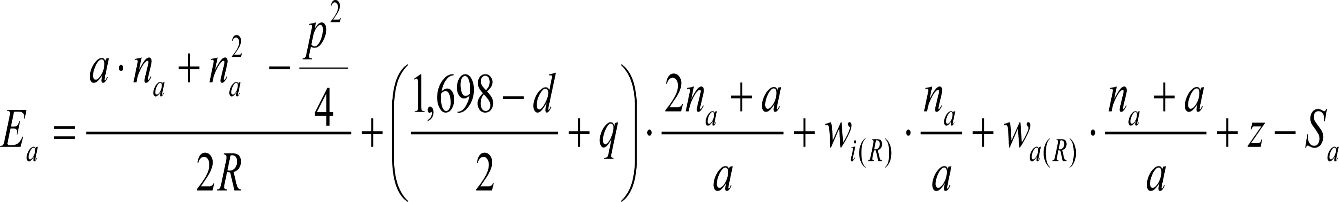
|
| Para curva de radio 150 ≤ R < 250 m: |
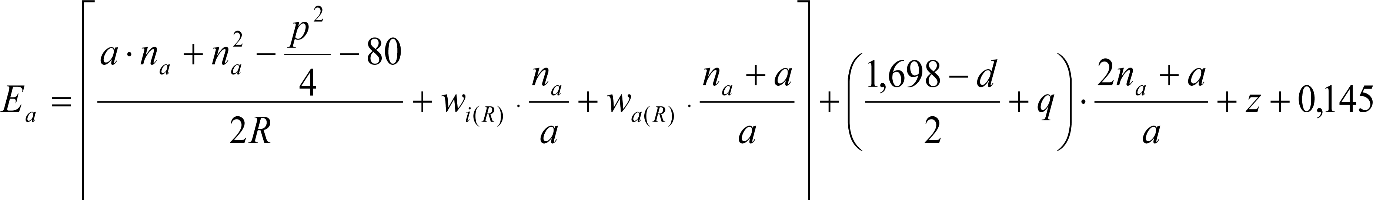
|
c) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones internas Ei
En este caso: 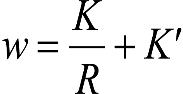 . Las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=250 o 150 m).
. Las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=250 o 150 m).
Si: 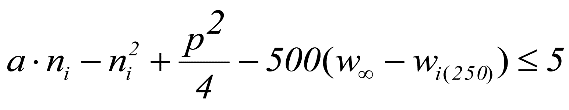 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
|
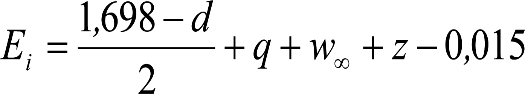
|
|
Si: 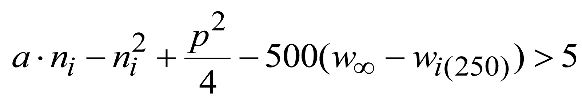 ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |
|
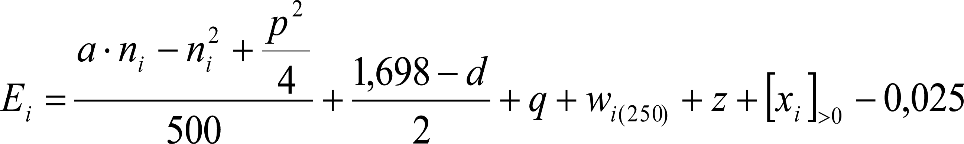
|
|
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
|
d) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones externas Ea
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
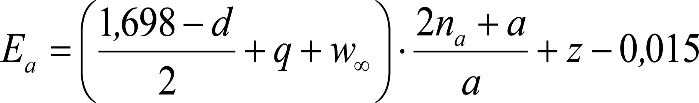
|
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |

|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
2.7.3.2.2 Material remolcado montado sobre bogies
Se consideran indistintamente dos bogies portadores o cuasiportadores.
a) Caso general. Reducción en secciones internas Ei
Para cada punto del vehículo el valor de la reducción Ei que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.
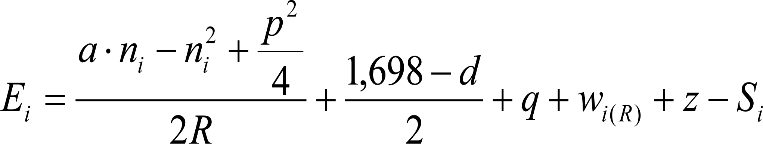
o bien, considerando los distintos salientes Si para partes altas y bajas:
| Para recta R = ∞: |
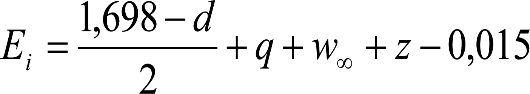
|
| Para curva de radio R ≥ 250 m: |

|
| Para curva de radio 150 ≤ R < 250 m: |

|
b) Caso general. Reducción en secciones externas Ea
Para cada punto del vehículo el valor de la reducción Ea que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.
La reducción considerando los distintos salientes Sa para partes altas y bajas será:
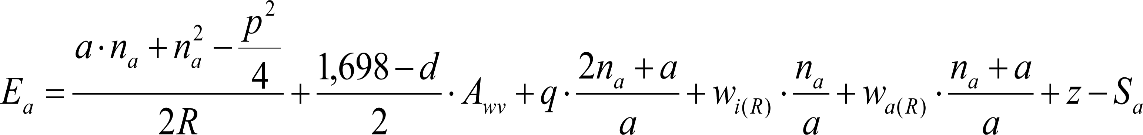
| Para recta R = ∞: |
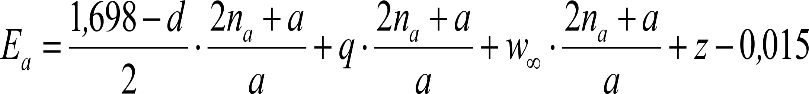
|
| Para curva de radio R ≥ 250 m: | |
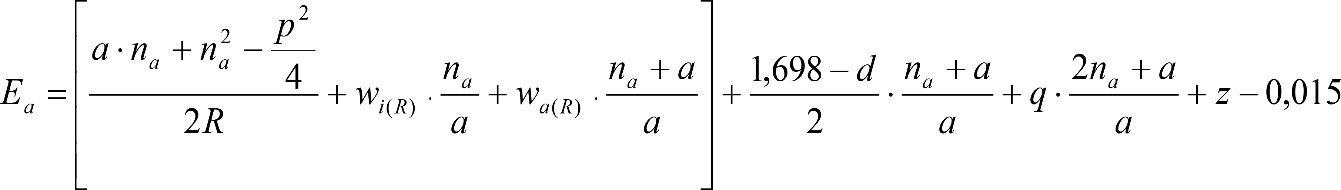
|
|
|
Para curva de radio 150 ≤ R < 250 m: |
|

|
|
c) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones internas Ei
En este caso: 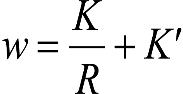 , y las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=250 o 150 m).
, y las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=250 o 150 m).
Si: 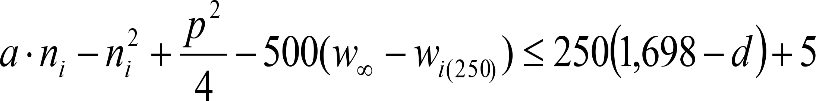 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
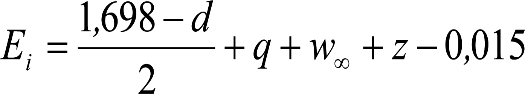
|
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |

|
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
|
d) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones externas Ea Si: |

|
|
Si: |
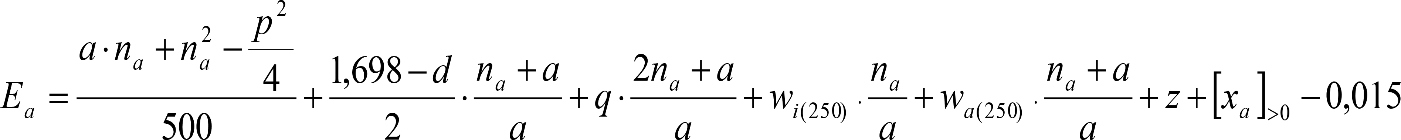
|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
e) Caso particular de vagones con bogies. Secciones internas Ei
En este caso, la holgura es constante, es decir, w∞= wi(R)= wa(R) = w.
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |

|
|
Si: |

|
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
f) Caso particular de vagones con bogies. Secciones externas Ea
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |

|
Si: 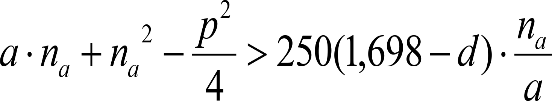 ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |

|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
2.7.3.2.3 Vagones sin bogies
Las reducciones se obtendrán particularizando las de material motor, con p=0 y w∞= wi(R)= wa(R) = w= 0 (al no existir bogies).
a) Reducción en secciones internas Ei
Si: 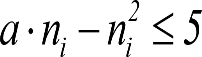 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
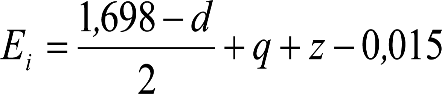
|
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |

|
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
b) Reducción en secciones externas Ea
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |

|
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |
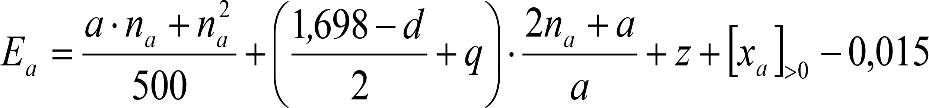
|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
2.7.3.2.4 Vehículos autopropulsados
Se utilizarán las fórmulas de reducción del cuadro 2.11, en función del coeficiente de adherencia rueda-carril (μ).
| Tipo de bogies | Valor de μ de cada bogie | Posición de rodadura sobre la vía | Fórmulas de reducción definidas en apartado |
|---|---|---|---|
| Dos bogies motores | μ ≥ 0,2 | Casos 2 y 5 del cuadro 2.4 | 2.7.3.2.1 |
| Dos bogies cuasi-portadores | 0 <μ < 0,2 | Casos 2 y 7 del cuadro 2.4 | 2.7.3.2.2 |
| Un bogie cuasi-portador y otro portador |
0 <μ < 0,2 μ = 0,2 |
||
| Dos bogies portadores | μ = 0,2 | ||
| Un bogie motor y otro portador |
μ ≥ 0,2 μ = 0,2 |
Casos 3 y 6 del cuadro 2.4 |
2.7.3.2.41 2.7.3.2.11 |
| Un bogie motor y otro cuasi-portador |
μ ≥ 0,2 0 <μ < 0,2 |
||
|
Los valores obtenidos de las fórmulas de reducción para vehículos motores y autopropulsados son parecidos. En general se utilizan las de vehículos motores, reservando las fórmulas de autopropulsados para aquellos casos en que la menor reducción obtenida sea significativa (0 a 12,5 mm según la sección considerada del vehículo), lo cual ocurre en el centro y extremos de la caja. |
|||
|
Cuadro 2.11. Fórmulas de reducción aplicables a los vehículos autopropulsados |
|||
La potencia de los vehículos autopropulsados es generalmente inferior a la de las locomotoras. Al existir un bogie motor y otro portador, sus características serán diferentes.
Se denomina:
p, w∞, wi, wa: empate y holguras del bogie motor.
p’, w’∞, w’i(R), w’a(R): empate y holguras del bogie portador.
nμ: distancia desde la sección interior considerada, hasta el pivote del bogie motor.
a) Reducción en secciones internas Ei
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
a.1) En recta:
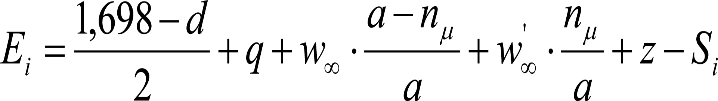
o bien, considerando el saliente Si:
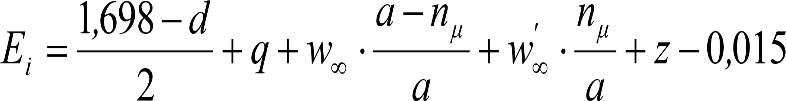
a.2) En curva:

o bien, considerando los distintos salientes Si:
| Para curvas de radio R=250 ó 150 m: |
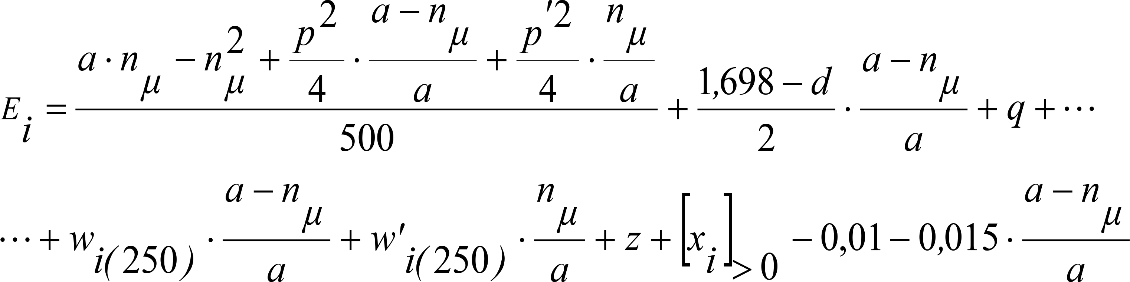
|
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
b) Reducción en secciones externas lado bogie motor Ea
En este caso el bogie motor va delante del bogie portador en el sentido de la marcha.
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
b.1) En recta:

o bien, considerando el saliente Sa:
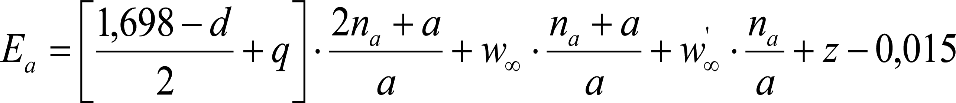
b.2) En curva:

o bien, considerando los distintos salientes Sa:
| Para curvas de radio R=250 ó 150 m: |
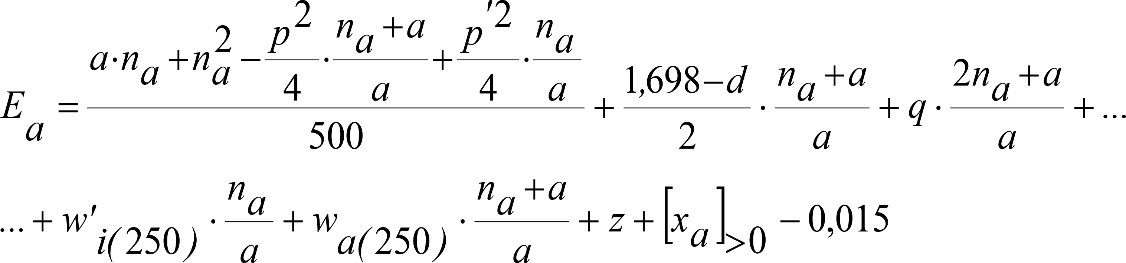
|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
c) Reducción en secciones externas lado bogie portador Ea
En este caso el bogie portador va delante del bogie motor en el sentido de la marcha.
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
c.1) En recta:
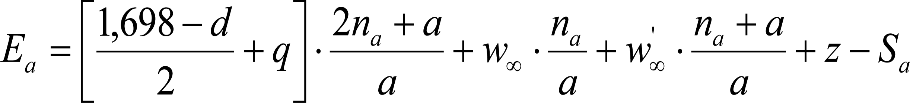
o bien, considerando el saliente Sa:
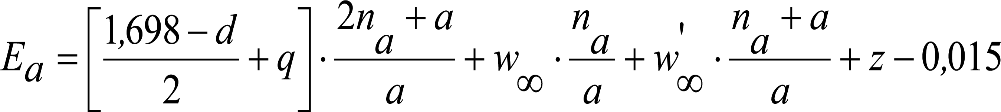
c.2) En curva:
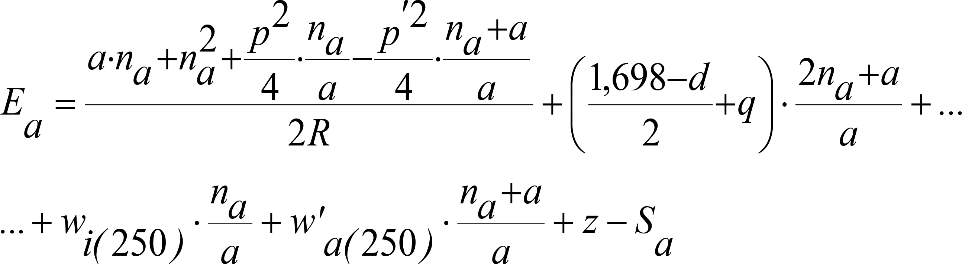
o bien, considerando los distintos salientes Sa:
| Para curvas de radio R=250 ó 150: |

|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
2.7.3.3 Fórmulas de reducción para gálibos GEA16 y GEB16, con gálibo de partes bajas GEI1 y GEI2
Para h ≤ 3,32 m se aplicarán las fórmulas del apartado 2.7.3.1.
Para h > 3,32 m se aplicarán las fórmulas indicadas a continuación.
2.7.3.3.1 Material motor
a) Caso general. Reducción en secciones internas Ei
Para cada punto del vehículo el valor de la reducción Ei que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.
En el caso de recta R = ∞ se aplicará la fórmula indicada en el apartado 2.7.3.1.1.
| Para curvas de radio R ≥ 250 m: |
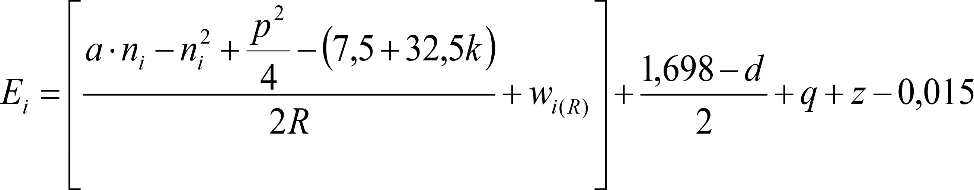
|
| Para curvas de radio 150 ≤ R < 250 m: |
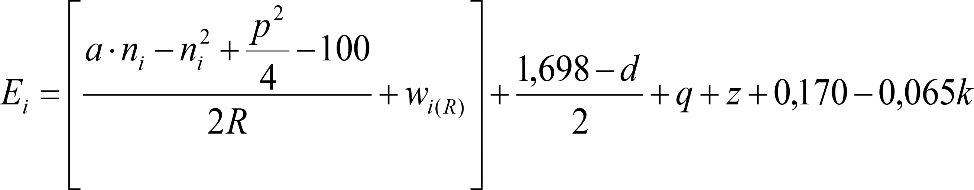
|
b) Caso general. Reducción en secciones externas Ea
Para cada punto del vehículo el valor de la reducción Ea que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.
En el caso de recta R = ∞ se aplicará la fórmula indicada en el apartado 2.7.3.1.1.
| Para curvas de radio R ≥ 250 m: |

|
| Para curvas de radio 150 ≤ R < 250 m: |
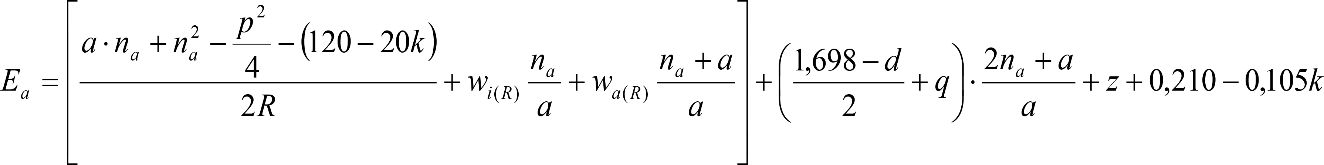
|
c) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones internas Ei
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
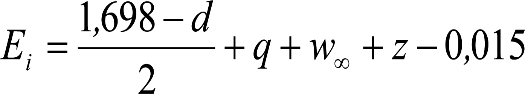
|
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |
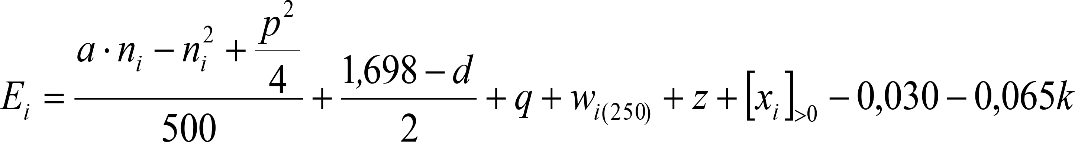
|
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
d) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones externas Ea
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |

|
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |

|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
2.7.3.3.2 Material remolcado montado sobre bogies
a) Caso general. Reducción en secciones internas Ei
Para cada punto del vehículo el valor de la reducción Ei que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.
En el caso de recta R = ∞ se aplicará la fórmula indicada en el apartado 2.7.3.1.2.
| Para curvas de radio R ≥ 250 m: |
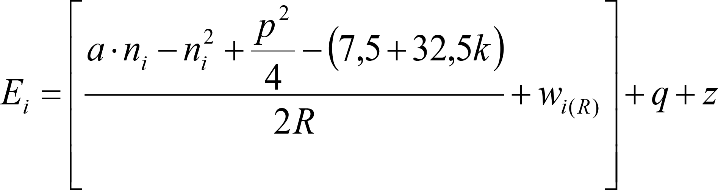
|
| Para curvas de radio 150 ≤ R < 250 m: |
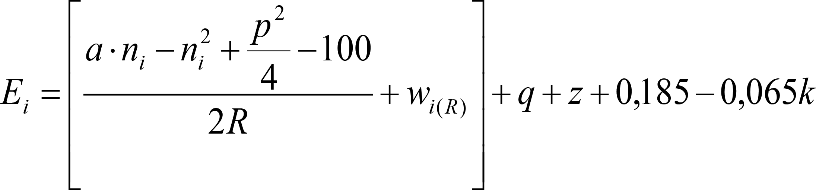
|
b) Caso general. Reducción en secciones externas Ea
Para cada punto del vehículo el valor de la reducción Ea que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.
En el caso de recta R = ∞ se aplicará la fórmula indicada en el apartado 2.7.3.1.2.
| Para curvas de radio R ≥ 250 m: | |
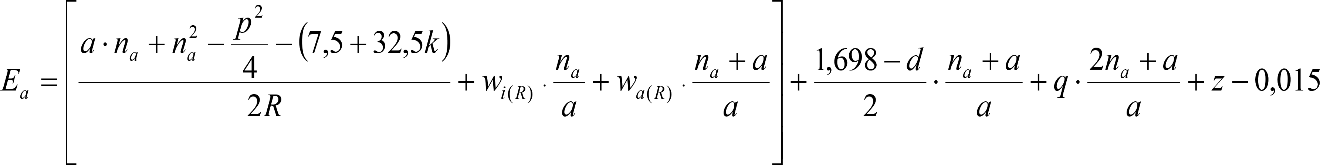
|
|
| Para curvas de radio 150 ≤ R < 250 m: | |
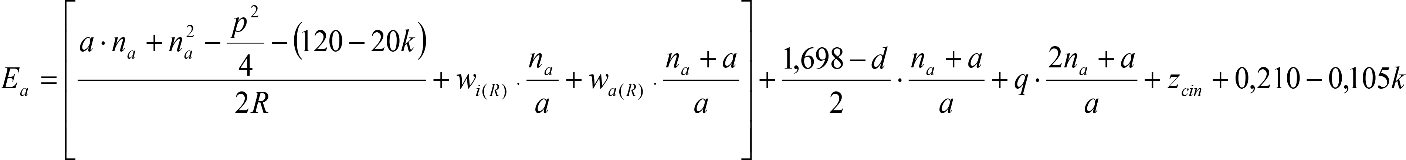
|
|
c) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones internas Ei
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
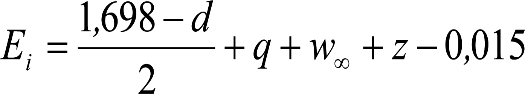
|
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |

|
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
d) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones externas Ea
Si: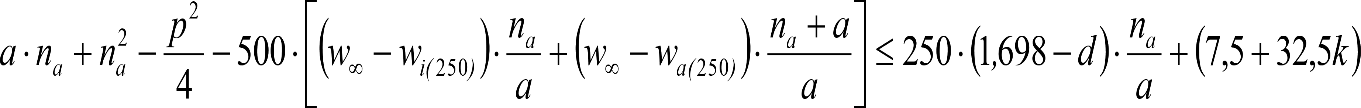 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
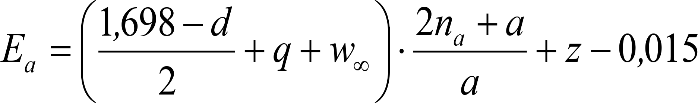
|
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |
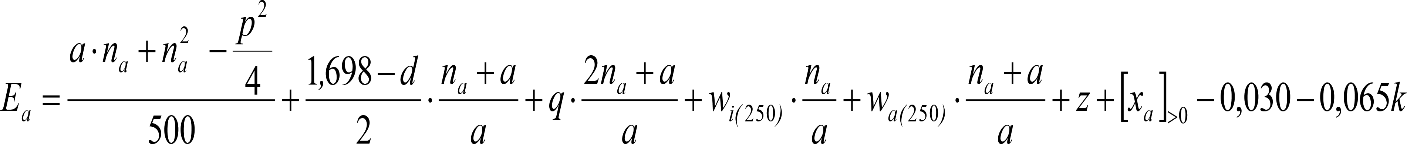
|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
e) Caso particular de vagones con bogies. Secciones internas Ei
En este caso, la holgura es constante, es decir, w∞= wi(R)= wa(R) = w.
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |

|
Si: 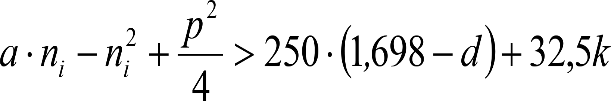 ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |

|
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
f) Caso particular de vagones con bogies. Secciones externas Ea
Si: ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |

|
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |
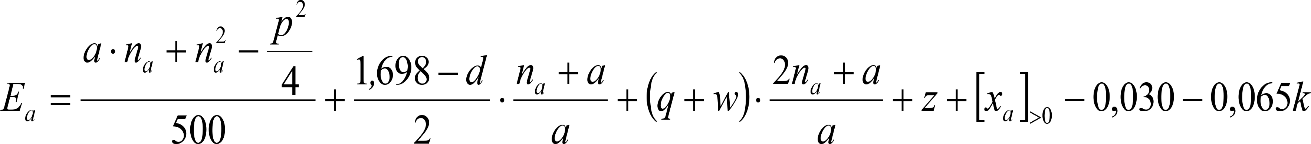
|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
2.7.3.3.3 Vagones sin bogies
Las reducciones se obtendrán particularizando las de material motor, con p=0 y w∞= wi(R)= wa(R) = w= 0 (al no existir bogies).
a) Reducción en secciones internas Ei
Si: 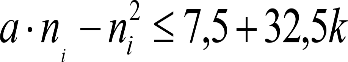 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
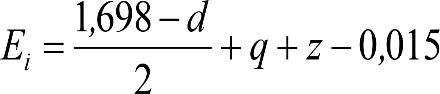
|
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |

|
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
b) Reducción en secciones externas Ea
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
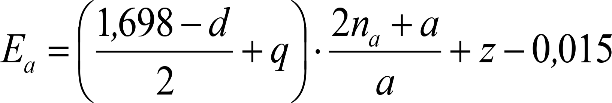
|
Si:  ⇒ La máx. reducción se da en curva (R=250 ó 150 m) ⇒ La máx. reducción se da en curva (R=250 ó 150 m) |

|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
2.7.3.3.4 Vehículos autopropulsados
Se utilizarán las fórmulas de reducción indicadas en el cuadro 2.12, en función del coeficiente de adherencia rueda-carril (μ).
| Tipo de bogies | Valor de μ de cada bogie | Posición de rodadura sobre la vía | Fórmulas de reducción definidas en apartado |
|---|---|---|---|
| Dos bogies motores | μ ≥ 0,2 | Casos 2 y 5 del cuadro 2.4 | 2.7.3.3.1 |
| Dos bogies cuasi-portadores | 0 <μ < 0,2 | Casos 2 y 7 del cuadro 2.4 | 2.7.3.3.2 |
| Un bogie cuasi-portador y otro portador |
0 <μ < 0,2 μ = 0,2 |
||
| Dos bogies portadores | μ = 0,2 | ||
| Un bogie motor y otro portador |
μ ≥ 0,2 μ = 0,2 |
Casos 3 y 6 del cuadro 2.4 |
2.7.3.3.41 2.7.3.3.11 |
| Un bogie motor y otro cuasi-portador |
μ ≥ 0,2 0 <μ < 0,2 |
||
| Los valores obtenidos de las fórmulas de reducción para vehículos motores y autopropulsados son parecidos. En general se utilizan las de vehículos motores, reservando las fórmulas de autopropulsados para aquellos casos en que la menor reducción obtenida sea significativa (0 a 12,5 mm según la sección considerada del vehículo), lo cual ocurre en el centro y extremos de la caja. | |||
|
Cuadro 2.12. Fórmulas de reducción aplicables a los vehículos autopropulsados |
|||
a) Reducción en secciones internas Ei
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
a.1) En recta

a.2) En curva
| Para curvas de radio R=250 ó 150 m: |

|
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
b) Reducción en secciones externas lado bogie motor Ea
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
b.1) En recta

b.2) En curva
| Para curvas de radio R=250 ó 150 m: |

|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
c) Reducción en secciones externas lado bogie portador Ea
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
c.1) En recta

c.2) En curva
| Para curvas de radio R=250 ó 150 m: |
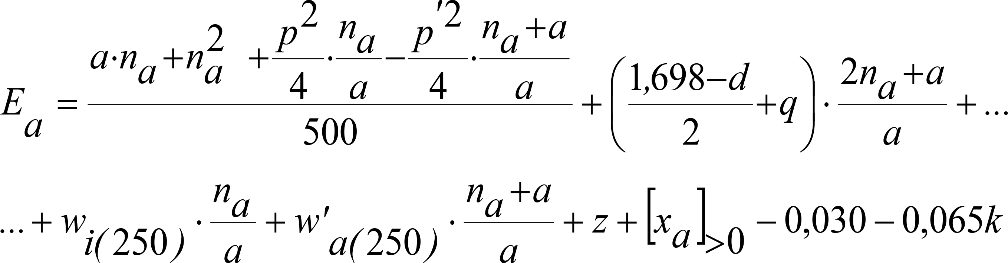
|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
2.7.3.4 Fórmulas de reducción para los gálibos GEA16 y GEB16, con gálibo de partes bajas GEI3
Para h ≥ 0,4 m se aplicarán las fórmulas del apartado 2.7.3.3.
Para h ≤ 0,25 m se aplicarán las fórmulas del apartado 2.7.3.2.
Para 0,25 < h < 0,4 m se realizará una interpolación entre los valores obtenidos para h=0,25 m y h=0,4 m.
2.7.4 CÁLCULO DEL GÁLIBO DE VEHÍCULOS DE CAJA INCLINABLE
Se utilizarán las expresiones del apartado 2.4 considerando los siguientes parámetros:
– L = 1,733 m.
– Ic = 0,175 m.
– l = lmáx = lN + 0,03 = 1,698 m.
2.7.5 CÁLCULO DEL GÁLIBO DEL PANTÓGRAFO EN POSICIÓN DE CAPTACIÓN
Los parámetros considerados para el cálculo del gálibo del pantógrafo serán:
– lN = 1,668 m.
– L = 1,733 m.
– D’o = I’o = ![]()
– Dmáx = Imáx = 0,160 m.
– s’o = 0,225.
– h’co = 0,5 m.
– Salientes del vehículo real: 
Siendo: 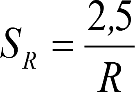 y
y 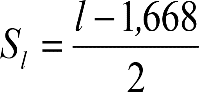
– Altura máxima de verificación del gálibo: h’o = 6,5 m.
– Altura mínima de verificación del gálibo: h’u = 5 m.
– Desplazamientos laterales máximos del vehículo tipo con pantógrafo, a ambos lados de su posición media, para las dos alturas de verificación:
– Para la altura máxima h’o: e*po = 0,150 m.
– Para la altura mínima h’u: e*pu = 0,110 m.
– Para una altura intermedia h: 
Con el pantógrafo en posición de captación, se considerarán dos casos:
– Caso general: Vehículo con holguras no variables linealmente con la curvatura. Se analizarán las situaciones de vehículo en recta R = ∞ y en curvas de R = 150 m y de otros R en los que la variación de w presente alguna discontinuidad.
– Caso particular: Vehículo con holgura variable linealmente con la curvatura 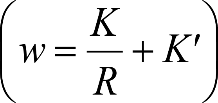 . Se analizarán las situaciones de vehículo en recta R = ∞ y en curva de R = 150 m.
. Se analizarán las situaciones de vehículo en recta R = ∞ y en curva de R = 150 m.
2.7.5.1 Vehículos convencionales
2.7.5.1.1 Secciones internas
Se considera la situación de vehículo parado en vía peraltada.
a) Para s ≤ 0,225
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):

Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):
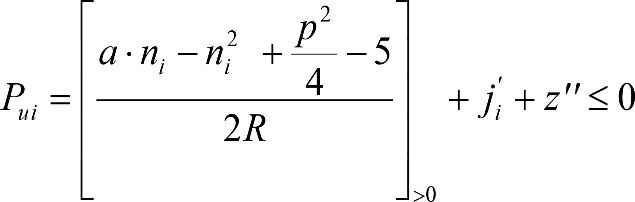
siendo:

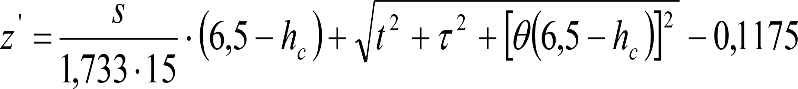

b) Para s > 0,225
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):

Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):

siendo:

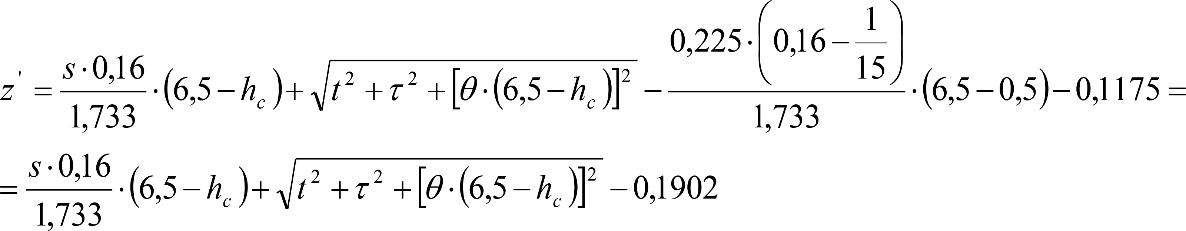

2.7.5.1.2 Secciones externas
Se considera la situación de vehículo circulando con insuficiencia de peralte.
a) Para s ≤ 0,225
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):
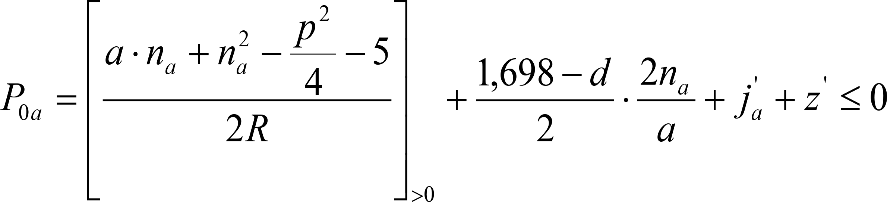
Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):
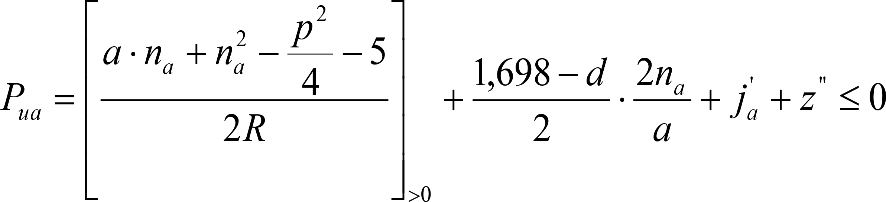
siendo:

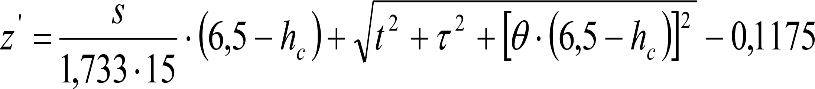
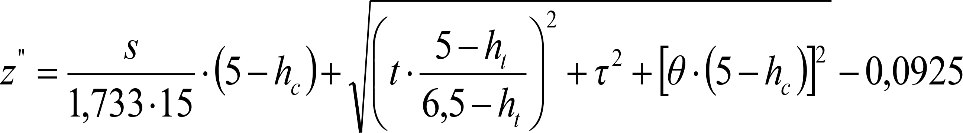
b) Para s > 0,225
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):

Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):

siendo:
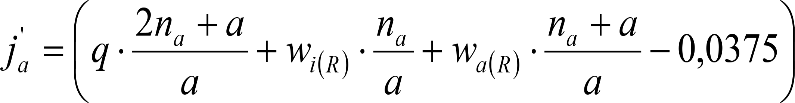
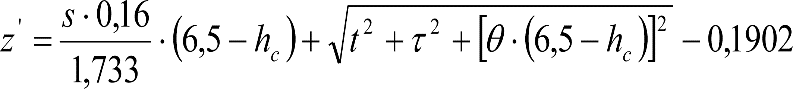

2.7.5.2 Vehículos de caja inclinable
2.7.5.2.1 Pantógrafos independientes del sistema de inclinación de la caja
a) Secciones internas
La verificación se realizará en recta, al tratarse de la situación más desfavorable, por lo tanto wa corresponde al valor w∞.
Para sn ≤ s’0
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):
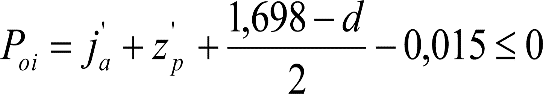
Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):
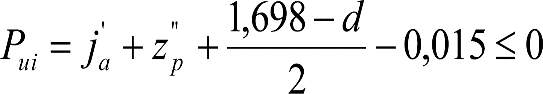
siendo:
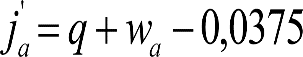
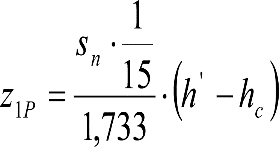
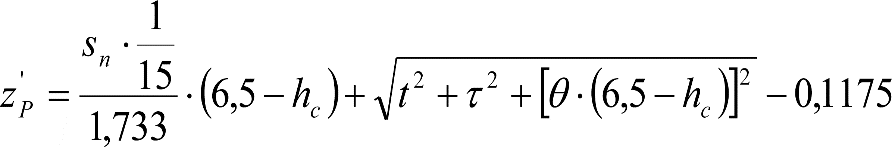

siendo sn el coeficiente de flexibilidad de la estructura portante del pantógrafo.
Para sn> s’0
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):
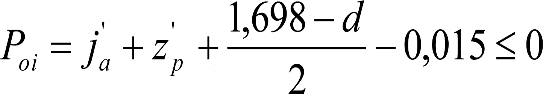
Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):
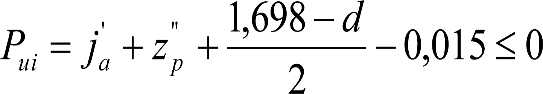
siendo:
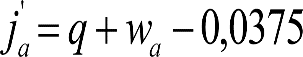
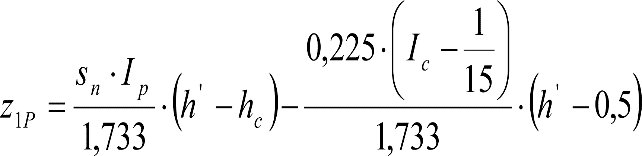
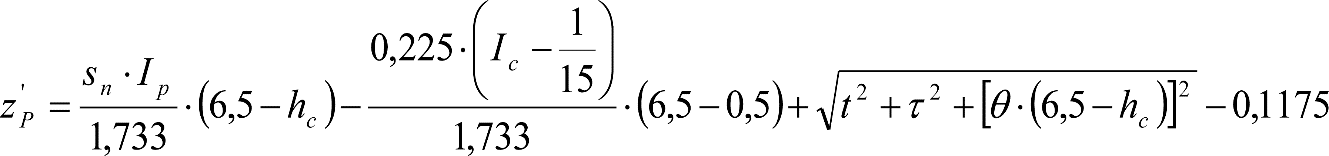
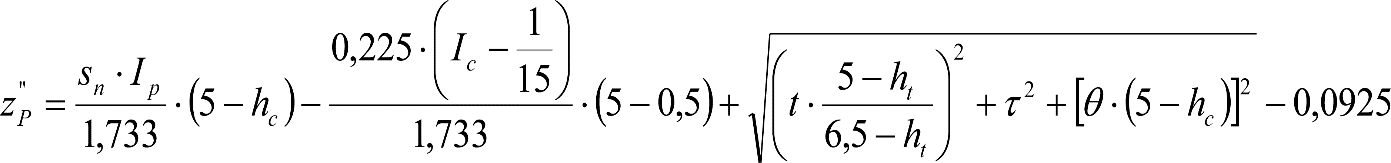
b) Secciones externas
Para sn ≤ s’0
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):
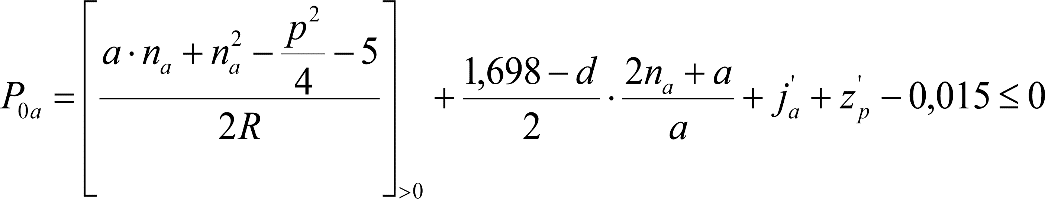
Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):


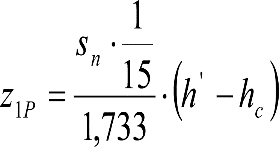
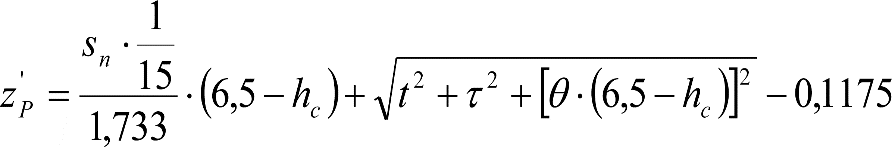
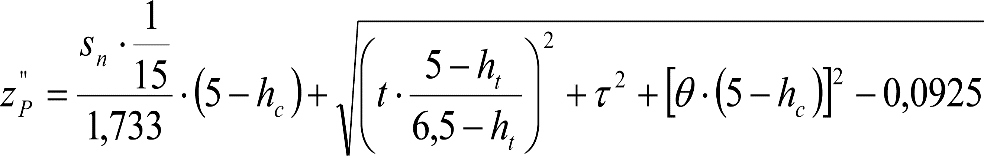
Para sn> s’0
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):
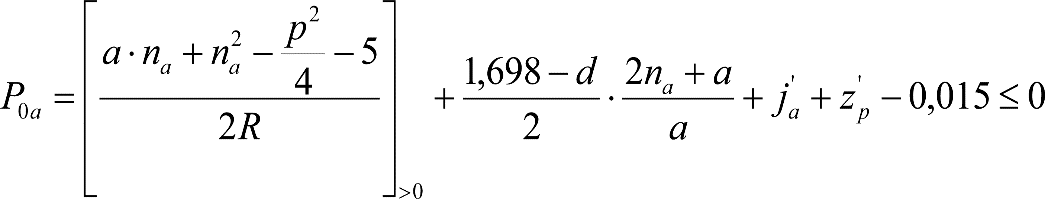
Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):

La verificación se realizará con el valor de R que maximiza los valores de Poa y Pua.
siendo:

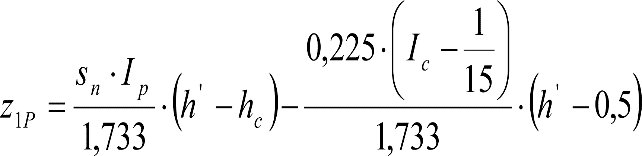
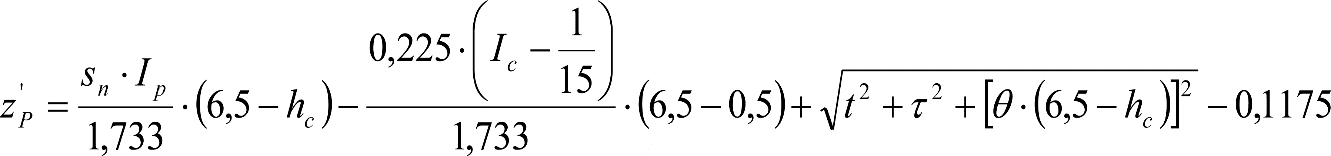
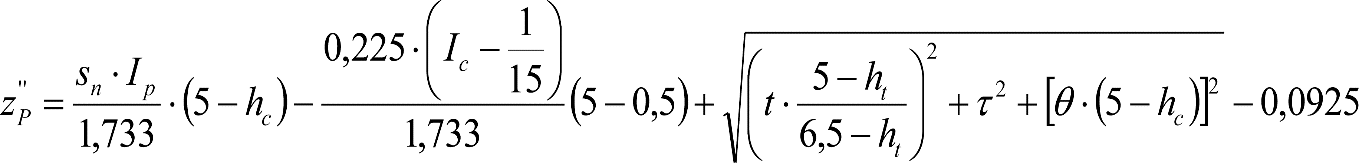
2.7.5.2.2 Vehículos con pantógrafos dependientes del sistema de inclinación de la caja
a) Secciones internas
La verificación se realizará en recta, al tratarse de la situación más desfavorable, por lo tanto wa corresponde al valor w∞.
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):
Cuando:


Cuando:
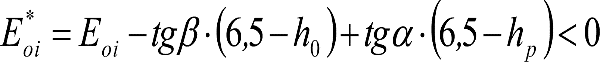

Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):
Cuando:
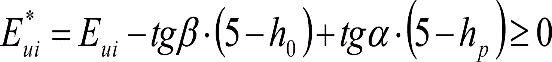

Cuando:
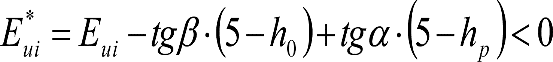
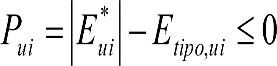
b) Secciones externas
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):
Cuando:
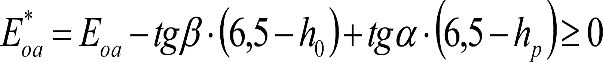
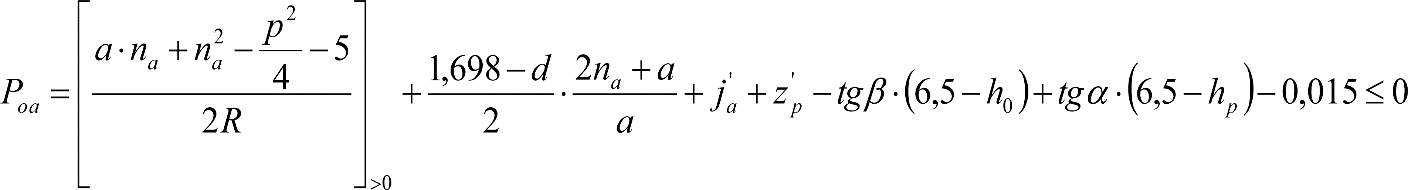
Cuando:

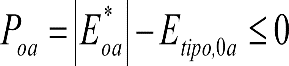
Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):
Cuando:
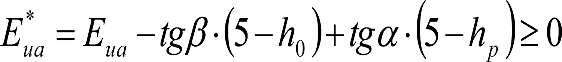

Cuando:

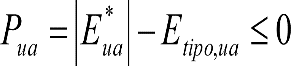
2.7.6 SITUACIÓN DE PELDAÑOS
Se adoptarán los valores de δv+,δv-,δhy bqo indicados en el cuadro 2.13.
| N.º de peldaños | Tipo de alineación de vía | δv+(mm) | δv-(mm) | δh(mm) | bqo(mm) |
|---|---|---|---|---|---|
| 1 | Recta | 230 | 160 | 270 | 1.720 |
| R= 300 m | 230 | 160 | 360 | 1.732,5 | |
| ≥ 2 | Recta | 230 | 160 | 450 | 1.720 |
| R= 300 m | 230 | 160 | 540 | 1.732,5 | |
|
Cuadro 2.13. Situación de peldaños |
|||||
2.8 APLICACIÓN A LÍNEAS CON ANCHO ESTÁNDAR EUROPEO
2.8.1 CONTORNOS DE REFERENCIA
Se consideran los siguientes contornos de referencia en las partes altas:
– GA
– GB
– GC
Se consideran los siguientes contornos de referencia en las partes bajas:
– GI1: material rodante apto para circular por vías equipadas con frenos de vía en posición activa y lomos de asno de las estaciones de clasificación.
– GI2: material rodante no apto para circular por vías equipadas con frenos de vía en posición activa ni lomos de asno de las estaciones de clasificación.
Los vehículos motores de maniobras utilizados en las estaciones de clasificación podrán tener el gálibo GI2 si van a pasar por los lomos de asno con los frenos de vía en posición no activa.
– GI3: material rodante apto para circular por vías acondicionadas para transporte mediante autopista ferroviaria.
2.8.1.1 Contornos de referencia de las partes altas
El contorno de referencia de las partes altas de los gálibos GA, GB y GC se define en la figura 2.36.
|
Figura 2.36. Contornos de referencia de los gálibos cinemáticos GA, GB y GC. Partes altas |
2.8.1.2 Contornos de referencia de las partes bajas
2.8.1.2.1 GI1
La figura 2.37 define el contorno de referencia del gálibo cinemático GI1.
|
a zona para los órganos no asociados con las ruedas b zona para los órganos en la proximidad inmediata de las ruedas c zona de extracción de los calces de frenado normalizados. Los obstáculos no deben penetrar esta zona. d zona para las ruedas y las partes que entren en contacto con el carril (patines de freno) e zona ocupada exclusivamente por las ruedas. f zona de frenos de vía en posición no activa, estando prohibido situar cualquier otro obstáculo. 1 Límite que no se puede exceder, de las partes situadas en la zona exterior de los ejes extremos (quitapiedras, expendedores de arena, etc) para el paso sobre los detonadores (zona b). Sin embargo, este límite no necesita ser respetado por las partes situadas entre las ruedas, siempre que permanezcan dentro de la estela de las ruedas (zona d). 2 Anchura máxima teórica del perfil de la pestaña en el caso de los contracarriles. La cota indicada de 37,5 mm es el mínimo valor que debe ser respetado en todo momento a fin de permitir el paso de la pestaña de la rueda. Ningún obstáculo deberá penetrar en éste área. Esta cota define la posición límite de la cara activa del contracarril. 3 Posición límite efectiva de la cara exterior de la rueda y de los órganos asociados con la rueda. 4 Esta cota representa igualmente la altura máxima de los calces de frenado normalizados, utilizadas para decelerar o inmovilizar el material. 5 Ninguna parte del material rodante debe penetrar en la zona c. 6 Posición límite efectiva de la cara interna de la rueda, cuando el eje se empuja contra el carril opuesto. Esta dimensión varía con el aumento del ancho de vía En el ancho definido por 58+(l-1435), los obstáculos deberán situarse por debajo de 36 mm bajo el plano de rodadura más el desgaste permitido de los carriles. 7 Ampliación de la zona de extracción de los calces de frenado normalizados. 8 Plano de rodadura. Figura 2.37. Contornos de referencia del gálibo cinemático GI1. Partes bajas |
2.8.1.2.2 GI2
La figura 2.38 define el contorno de referencia del gálibo cinemático GI2.
|
a zona para los órganos no asociados con las ruedas b zona para los órganos en la proximidad inmediata de las ruedas c zona de las escobillas del sistema de repetición de señales (RS, cocodrilos) d zona para las ruedas y las partes que entren en contacto con el carril (patines de freno) e zona ocupada exclusivamente por las ruedas. 1 Límite que no se puede exceder, de las partes situadas en la zona exterior de los ejes extremos (quitapiedras, expendedores de arena, etc) para el paso sobre los detonadores (zona b). Sin embargo, este límite no necesita ser respetado por las partes situadas entre las ruedas, siempre que permanezcan dentro de la estela de las ruedas (zona d). 2 Anchura máxima teórica del perfil de la pestaña en el caso de los contracarriles. La cota indicada de 37,5 mm es el mínimo valor que debe ser respetado en todo momento a fin de permitir el paso de la pestaña de la rueda. Ningún obstáculo deberá penetrar en éste área. Esta cota define la posición límite de la cara activa del contracarril. 3 Posición límite efectiva de la cara exterior de la rueda y de los órganos asociados con la rueda. 4 Cuando el vehículo está inscrito en cualquier posición, en una vía en curva de radio R = 250 m (radio mínimo para la instalación del contacto fijo de vía) y con un ancho de vía de 1,465 m, ninguna parte del vehículo que pueda caer por debajo de 0,100 m por encima de la superficie de rodadura de los carriles, excepto las escobillas del sistema de repetición de señales (RS, cocodrilos), se debe encontrar a menos de 0,125 m del eje de la vía. Para los elementos montados bajo bogie el espacio a disponer debe ser igual a 0,150 m. 5 Posición límite efectiva de la cara interna de la rueda, cuando el eje se empuja contra el carril opuesto. Esta dimensión varía con el aumento del ancho de vía. En el ancho definido por 58+(l-1435), los obstáculos deberán situarse por debajo de 36 mm bajo el plano de rodadura más el desgaste permitido de los carriles. 6 Plano de rodadura. Figura 2.38. Contornos de referencia del gálibo cinemático GI2. Partes bajas |
2.8.1.2.3 GI3
La figura 2.39 define el contorno de referencia del gálibo cinemático GI3, en el caso de que el material rodante sea apto para circular por vías acondicionadas para transporte mediante autopista ferroviaria.
|
a zona para los órganos no asociados con las ruedas b zona para los órganos en la proximidad inmediata de las ruedas c zona de las escobillas del sistema de repetición de señales (RS, cocodrilos) d zona para las ruedas y las partes que entren en contacto con el carril (patines de freno) e zona ocupada exclusivamente por las ruedas 1 Límite que no se puede exceder, de las partes situadas en la zona exterior de los ejes extremos (quitapiedras, expendedores de arena, etc) para el paso sobre los detonadores(zona b). Sin embargo, este límite no necesita ser respetado por las partes situadas entre las ruedas, siempre que permanezcan dentro de la estela de las ruedas (zona d). 2 Anchura máxima teórica del perfil de la pestaña en el caso de los contracarriles. La cota indicada de 37,5 mm es el mínimo valor que debe ser respetado en todo momento a fin de permitir el paso de la pestaña de la rueda. Ningún obstáculo deberá penetrar en éste área. Esta cota define la posición límite de la cara activa del contracarril. 3 Posición límite efectiva de la cara exterior de la rueda y de los órganos asociados con la rueda. 4 Cuando el vehículo está inscrito en cualquier posición, en una vía en curva de radio R = 250 m (radio mínimo para la instalación del contacto fijo de vía) y con un ancho de vía de 1,465 m, ninguna parte del vehículo que pueda caer por debajo de 0,100 m por encima de la superficie de rodadura de los carriles, excepto las escobillas del sistema de repetición de señales (RS, cocodrilos), se debe encontrar a menos de 0,125 m del eje de la vía. Para los elementos montados bajo bogie el espacio a disponer debe ser igual a 0,150 m. 5 Posición límite efectiva de la cara interna de la rueda, cuando el eje se empuja contra el carril opuesto. Esta dimensión varía con el aumento del ancho de vía. En el ancho definido por 58+(l-1435), los obstáculos deberán situarse por debajo de 36 mm bajo el plano de rodadura más el desgaste permitido de los carriles. 6 Plano de rodadura. 7 Eje del contorno de referencia. 8 Cara interna del carril. Figura 2.39. Contornos de referencia del gálibo cinemático GI3 del material apto para circular por autopista ferroviaria. Partes bajas |
2.8.2 REGLAS ASOCIADAS
2.8.2.1 Desplazamientos verticales
Serán los indicados en el apartado 2.2.2, con las particularidades siguientes:
1) Los desplazamientos verticales a considerar en la determinación de la altura mínima sobre el plano de rodadura, solo se aplicarán a las partes bajas del vehículo situadas a una altura h ≤ 1.170 mm.
2) Los desplazamientos verticales a considerar en la determinación de la altura máxima sobre el plano de rodadura, solo se aplicarán a las partes altas del vehículo situadas a una altura h ≥ 3.250 mm (gálibos GA y GB) y h ≥ 3.550 mm (gálibo GC).
2.8.2.2 Holgura lateral entre eje de ruedas y vía
De la expresión del apartado 2.2.3.2.1 se tiene:
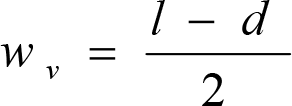
siendo:
l: ancho de vía. Se toma:
l = lmáx = lN + sobre ancho máximo = lN + 0,03 = 1,465m (caso general).
l = lN = 1,435m (caso de secciones internas en curva, tanto para vehículos remolcados con dos bogies portadores o cuasiportadores, como para vagones con bogies).
2.8.2.3 Desplazamientos por exceso o insuficiencia de peralte y disimetría
Se obtendrán particularizando las fórmulas de los apartados 2.2.3.3 y 2.2.3.4 para los valores siguientes:
hco = 0,5 m
L = 1,500 m
Io = Do= 0,050 m
Dmax = Imax= 0,200 m
a) Vehículos en general

donde:
![]() es valor absoluto, es decir, que si h<hc se toma hc-h.
es valor absoluto, es decir, que si h<hc se toma hc-h.
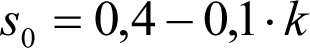 , donde k se define en el cuadro 2.16 en función del gálibo.
, donde k se define en el cuadro 2.16 en función del gálibo.
Finalmente:

b) Vagones equipados con bogies
– Si J ≤ 5 mm: 
– Si J > 5 mm:
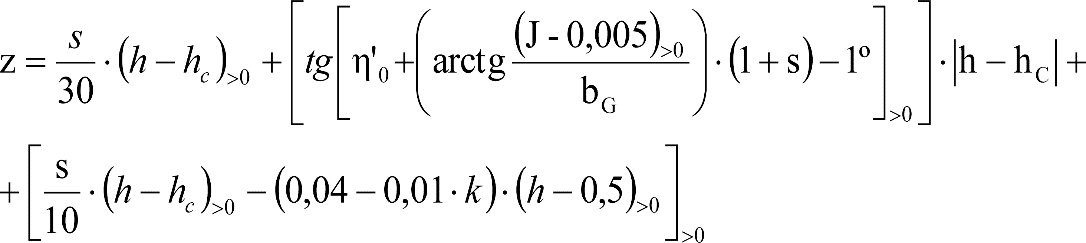
2.8.2.4 Salientes
Se adoptarán los salientes indicados en los cuadros 2.14 y 2.15 en función del gálibo en partes altas y bajas.
Como valor de l se tomará el indicado en el apartado 2.8.2.2.
| Salientes máximos para un ancho de vía l y para una altura h del punto considerado sobre el plano de rodadura | ||
|---|---|---|
| Gálibo | Radio | h ≤ 0,4 m |
|
GI1 GI2 |
250 ≤ R ≤ ∞ |
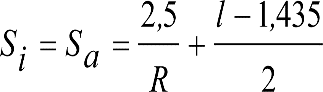
|
| 150 ≤ R < 250 |
|
|
| GI3 | 250 ≤ R ≤ ∞ |
|
| 150 ≤ R < 250 |
|
|
|
NOTA: Si = Lado interior de la curva (m); Sa = Lado exterior de la curva (m) |
||
|
Cuadro 2.15. Salientes de los gálibos GI1, GI2 y GI3. Partes bajas |
||
| GÁLIBO | Altura h (m) | s 0 | k |
|---|---|---|---|
| GC | Cualquier altura | 0,4 | 0 |
| GA | h ≤ 3,25 | 0,4 | 0 |
| 3,25 < h < 3,88 |
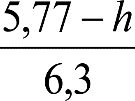
|
|
|
| h ≥ 3,88 | 0,3 | 1 | |
| GB | h ≤ 3,25 | 0,4 | 0 |
| 3,25 < h < 4,11 |

|
|
|
| h ≥ 4,11 | 0,3 | 1 | |
| GI1 | Cualquier altura | 0,4 | 0 |
| GI2 | Cualquier altura | 0,4 | 0 |
| GI3 | h ≤ 0,25 | 0,4 | 1 |
| 0,25 < h ≤ 0,4 | 0,4 |
|
|
|
Cuadro 2.16. Valores de s0 y k para los gálibos GA, GB, GC, GI1, GI2 y GI3 |
|||
2.8.3 CÁLCULO DEL GÁLIBO DEL MATERIAL
2.8.3.1 Fórmulas de reducción del gálibo GC, con gálibo de partes bajas GI1 y GI2
Se aplicarán las fórmulas definidas para los gálibos GHE16 y GEC16 en el apartado 2.7.3.1, con las siguientes modificaciones:
– El valor de lN = 1,668 m se sustituye por 1,435 m.
– El valor de l = 1,698 m se sustituye por 1,465 m.
2.8.3.2 Fórmulas de reducción del gálibo GC, con gálibo de partes bajas GI3
Se aplicarán las fórmulas definidas para los gálibos GHE16 y GEC16 en el apartado 2.7.3.2, con las siguientes modificaciones:
– El valor de lN = 1,668 m se sustituye por 1,435 m.
– El valor de l = 1,698 m se sustituye por 1,465 m.
2.8.3.3 Fórmulas de reducción para gálibos GA y GB, con gálibo de partes bajas GI1 y GI2
Para los gálibos GA y GB se aplicarán las fórmulas definidas en el apartado 2.7.3.1 para alturas h ≤ 3,25 m, y en el apartado 2.7.3.3 para alturas h > 3,25 m para los gálibos GEA16 y GEB16, respectivamente, con las siguientes modificaciones:
– El valor de lN = 1,668 m se sustituye por 1,435 m
– El valor de l = 1,698 m se sustituye por 1,465 m.
– El valor de k es el definido en el cuadro 2.16.
2.8.3.4 Fórmulas de reducción para gálibos GA y GB, con gálibo de partes bajas GI3
Para los gálibos GA y GB se aplicarán las fórmulas definidas para los gálibos GEA16 y GEB16, respectivamente, en el apartado 2.7.3.4, con las siguientes modificaciones:
– El valor de lN = 1,668 m se sustituye por 1,435 m
– El valor de l = 1,698 m se sustituye por 1,465 m.
– El valor de k es el definido en el cuadro 2.16.
2.8.4 CÁLCULO DEL GÁLIBO DE VEHÍCULOS DE CAJA INCLINABLE
Se utilizarán las expresiones del apartado 2.4 considerando los siguientes parámetros:
– L = 1,5 m.
– Ic = 0,150 m.
– l = lmáx = lN + 0,03 = 1,465 m.
2.8.5. CÁLCULO DEL GÁLIBO DEL PANTÓGRAFO EN POSICIÓN DE CAPTACIÓN
Los parámetros considerados para el cálculo del gálibo del pantógrafo serán:
– lN = 1,435 m.
– L = 1,500 m.
– D’o = I’o = ![]()
– Dmáx = Imáx = 0,200 m.
– s’o = 0,225.
– h’co =0,5 m.
– Salientes del vehículo real: 
Siendo: 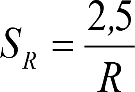 y
y 
– Altura máxima de verificación del gálibo: h’o = 6,5 m.
– Altura mínima de verificación del gálibo: h’u = 5 m.
– Desplazamientos laterales máximos del vehículo tipo con pantógrafo, a ambos lados de su posición media, para las dos alturas de verificación:
– Para la altura máxima h’o: e*po = 0,150 m.
– Para la altura mínima h’u: e*pu = 0,110 m.
– Para una altura intermedia h: 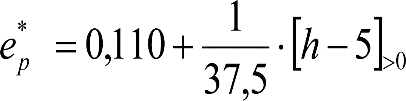
Con el pantógrafo en posición de captación, se considerarán dos casos:
∙ Caso general: Vehículo con holguras no variables linealmente con la curvatura. Se analizarán las situaciones de vehículo en recta R = ∞ y en curvas de R = 150 m y de otros R en los que la variación de w presente alguna discontinuidad.
∙ Caso particular: Vehículo con holgura variable linealmente con la curvatura 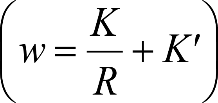 . Se analizarán las situaciones de vehículo en recta R = ∞ y en curva de R = 150 m.
. Se analizarán las situaciones de vehículo en recta R = ∞ y en curva de R = 150 m.
2.8.5.1 Vehículos convencionales
2.8.5.1.1 Secciones internas
Se considera la situación de vehículo parado en vía peraltada.
a) Para s ≤ 0,225
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):

Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):

siendo:
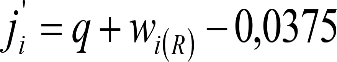

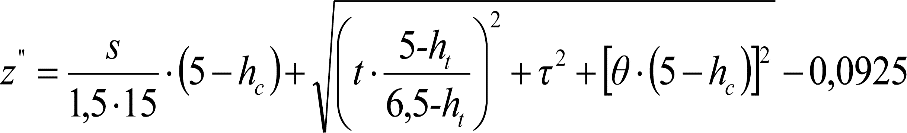
b) Para s > 0,225
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):
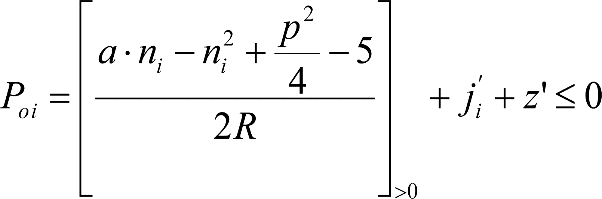
Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):
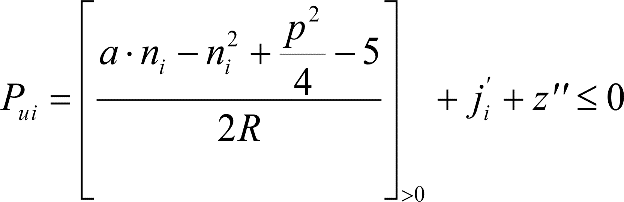
siendo:
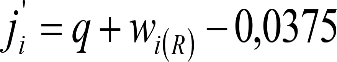
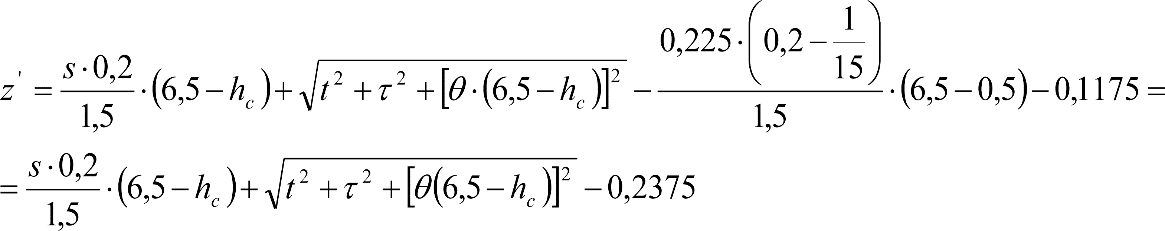
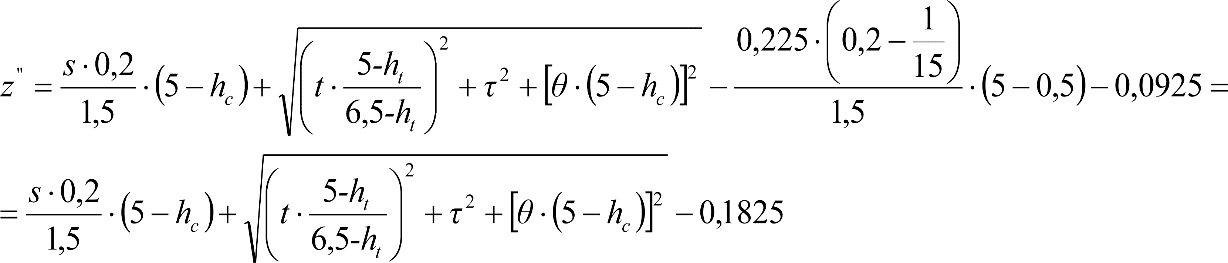
2.8.5.1.2 Secciones externas
Se considera la situación de vehículo circulando con insuficiencia de peralte.
a) Para s ≤ 0,225
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):

Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):

siendo:



b) Para s > 0,225
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):

Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):

siendo:
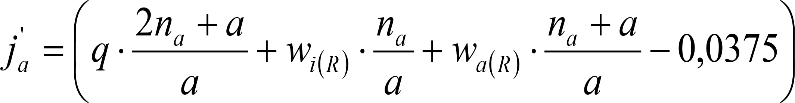

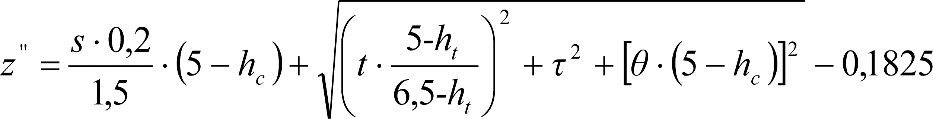
2.8.5.2 VEHÍCULOS DE CAJA INCLINABLE
2.8.5.2.1 Pantógrafos independientes del sistema de inclinación de la caja
a) Secciones internas
La verificación se realizará en recta, al tratarse de la situación más desfavorable, por lo tanto wa corresponde al valor w∞.
Para sn ≤ s’0
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):

Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):

siendo:
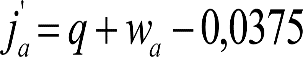
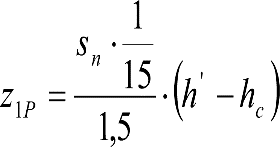
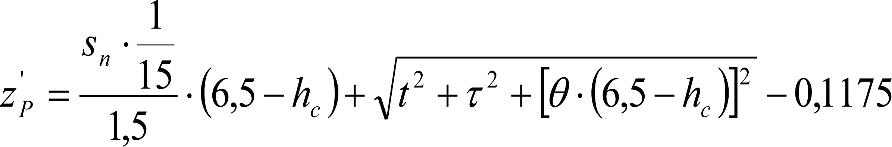
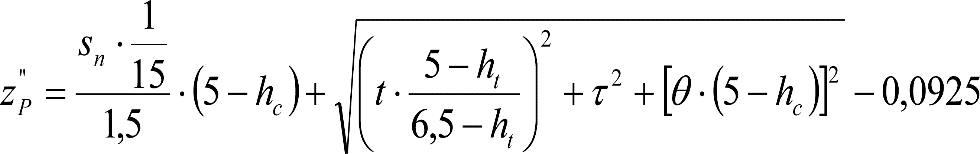
siendo sn el coeficiente de flexibilidad de la estructura portante del pantógrafo.
Para sn> s’0
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):

Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):

siendo:
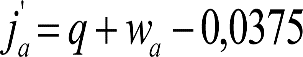

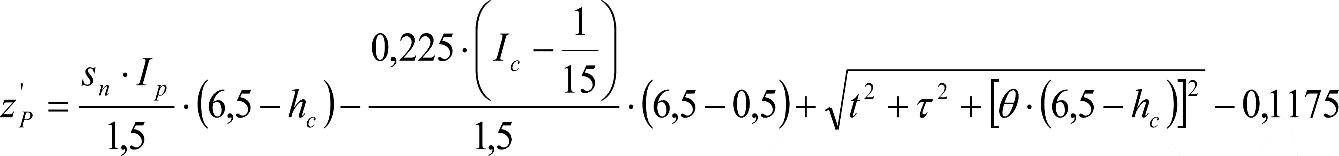

b) Secciones externas
Para sn ≤ s’0
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):

Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):
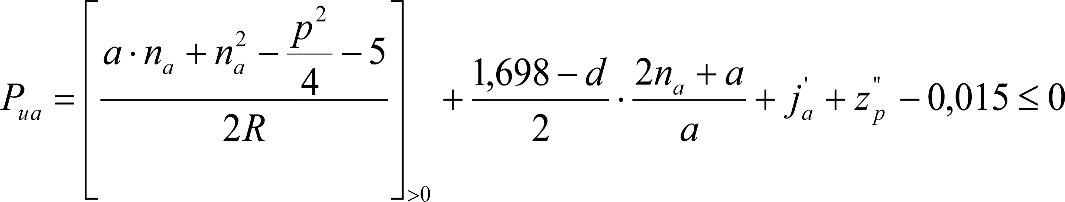
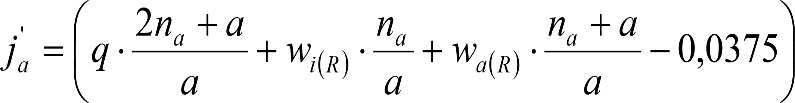

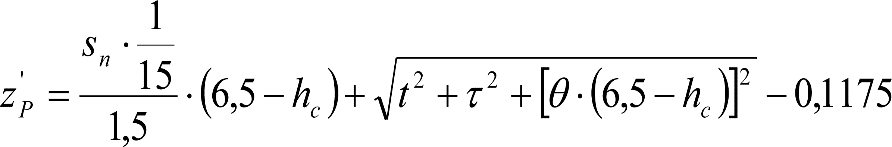
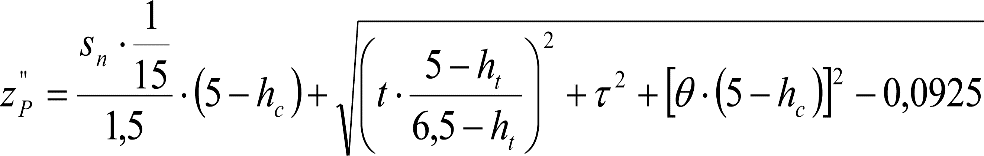
Para sn> s’0
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):
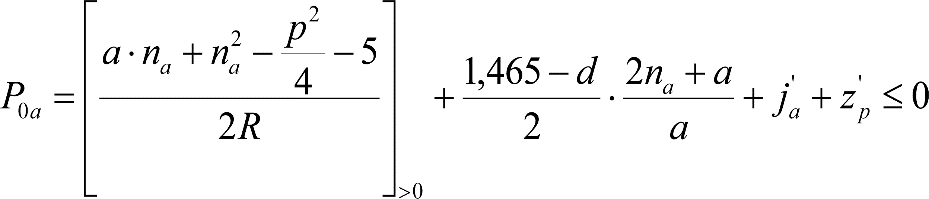
Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):

La verificación se realizará con el valor de R que maximiza los valores de Poa y Pua.
siendo:
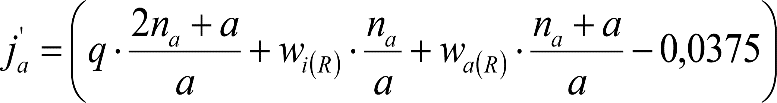
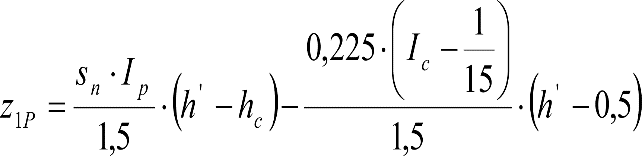

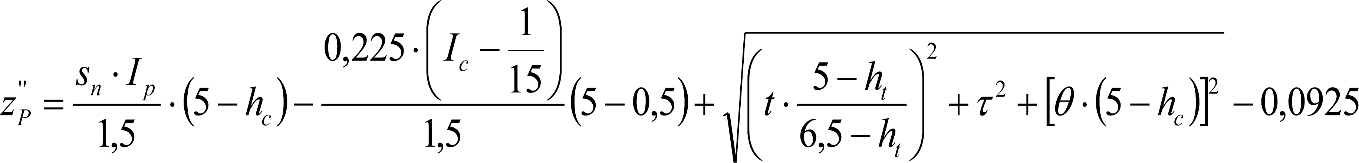
2.8.5.2.2 Vehículos con pantógrafos dependientes del sistema de inclinación de la caja
a) Secciones internas
La verificación se realizará en recta, al tratarse de la situación más desfavorable, por lo tanto wa corresponde al valor w∞.
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):
Cuando:

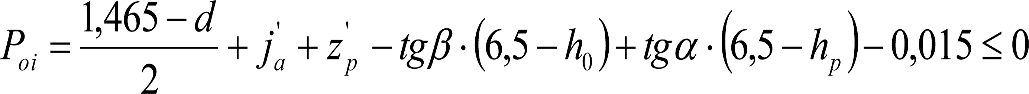
Cuando:


Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):
Cuando:
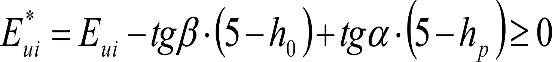
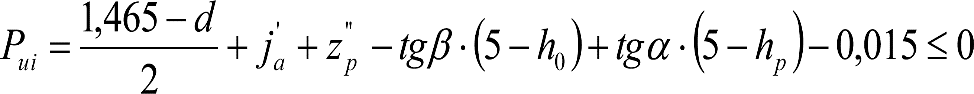
Cuando:
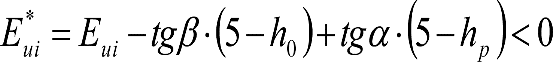

b) Secciones externas
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=6,5m):
Cuando:


Cuando:
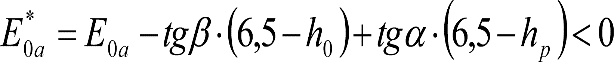
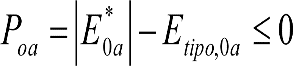
Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=5m):
Cuando:


Cuando:
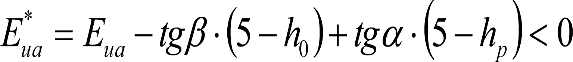
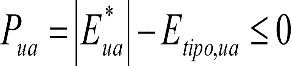
2.8.6 SITUACIÓN DE PELDAÑOS
Se adoptarán los valores de δv+,δv-,δhy bqo indicados en el cuadro 2.17.
| N.º de peldaños | Tipo de alineación de vía | δv+(mm) | δv-(mm) | δh(mm) | bqo(mm) |
|---|---|---|---|---|---|
| 1 | Recta | 230 | 160 | 200 | 1.650 |
| R= 300 m | 230 | 160 | 290 | 1.662,5 | |
| ≥ 2 | Recta | 230 | 160 | 380 | 1.650 |
| R= 300 m | 230 | 160 | 470 | 1.662,5 | |
|
Cuadro 2.17. Situación de peldaños |
|||||
2.9 APLICACIÓN A LÍNEAS CON ANCHO MÉTRICO
2.9.1 CONTORNOS DE REFERENCIA
Se consideran los siguientes contornos de referencia:
∙ GEE10, para material que circule por líneas electrificadas.
∙ GED10, para material que circule por líneas no electrificadas.
2.9.1.1 GEE10
2.9.1.1.1 Contorno de referencia de las partes altas
El contorno de referencia de las partes altas se define en la figura 2.40.
|
(1) Plano de rodadura NOTA Partes bajas definidas en la figura 2.41 Figura 2.40. Contorno de referencia del gálibo cinemático GEE10. Partes altas |
2.9.1.1.2 Contorno de referencia de las partes bajas
La figura 2.41 define el contorno de referencia de las partes bajas.
|
(1) Plano de rodadura l : Ancho de vía Figura 2.41. Contorno de referencia del gálibo cinemático GEE10. Partes bajas |
2.9.1.2 GED10
El contorno de referencia de las partes altas se define en la figura 2.42.
Para las partes bajas el contorno coincide con el definido para el gálibo GEE10.
|
(1) Plano de rodadura NOTA Partes bajas definidas en la figura 2.41 Figura 2.42. Contorno de referencia del gálibo cinemático GED10. Partes altas |
2.9.2 REGLAS ASOCIADAS
2.9.2.1 Desplazamientos verticales
Serán los indicados en el apartado 2.2.2 con las particularidades siguientes:
1) Los desplazamientos verticales a considerar en la determinación de la altura mínima sobre el plano de rodadura, solo se aplicarán a las partes bajas del vehículo situadas a una altura h ≤ 400 mm.
2) Los desplazamientos verticales a considerar en la determinación de la altura máxima sobre el plano de rodadura, solo se aplicarán a las partes altas del vehículo situadas a una altura h ≥ 3.550 mm.
2.9.2.2 Holgura lateral entre eje de ruedas y vía
De la expresión del apartado 2.2.3.2.1 se tiene:
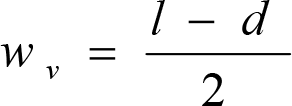
siendo:
l: ancho de vía. Se toma:
l = lmáx = lN + sobre ancho máximo = lN +0,03 = 1,030m (caso general).
l = lN = 1,000 m (caso de secciones internas en curva, tanto para vehículos remolcados con dos bogies portadores o cuasiportadores, como para vagones con bogies).
2.9.2.3 Desplazamientos por exceso o insuficiencia de peralte y disimetría
Se obtendrán particularizando las fórmulas de los apartados 2.2.3.3 y 2.2.3.4 para los valores siguientes:
hco = 0,5 m
L = 1,055 m
Io = Do= 0,070 m
Dmax = Imax = 0,120 m
so = 0,4
a) Vehículos en general:

donde:
![]() es valor absoluto, es decir, que si h<hc se toma hc-h.
es valor absoluto, es decir, que si h<hc se toma hc-h.
b) Vagones equipados con bogies:
∙ Si J ≤ 5 mm: 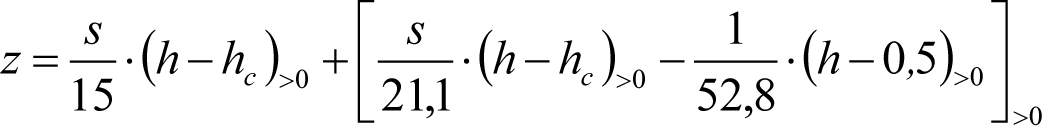
∙ Si J > 5 mm:
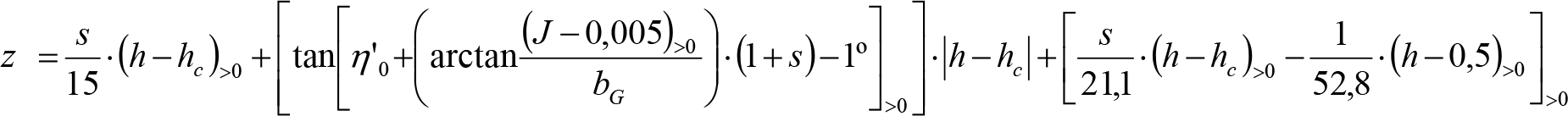
2.9.2.4 Salientes
Se adoptarán los salientes indicados en el cuadro 2.18 en función del gálibo.
Como valor de l se tomará el indicado en el apartado 2.9.2.2.
| Salientes máximos para un ancho de vía l y para una altura h del punto considerado sobre el plano de rodadura | ||||
|---|---|---|---|---|
| Gálibo | Radio | h ≤ 0,4 m | h > 0,4 m | Zona de pantógrafos |
|
GEE10 GED10 |
100 ≤ R ≤ ∞ |

|

|
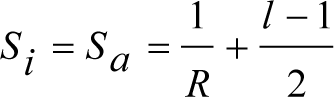
|
| 80 ≤ R < 100 |
|
|
||
|
NOTA: Si = Lado interior de la curva (m); Sa = Lado exterior de la curva (m) |
||||
|
Cuadro 2.18. Salientes de los gálibos GEE10 y GED10 |
||||
2.9.3 CÁLCULO DEL GÁLIBO DEL MATERIAL
2.9.3.1 Fórmulas de reducción para los gálibos GEE10 y GED10
2.9.3.1.1 Material motor
Se consideran dos bogies motores.
a) Caso general. Reducción en secciones internas Ei
Para cada punto del vehículo el valor de la reducción Ei que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.

o bien, considerando los distintos salientes Si para partes altas y bajas:
| Para recta R = ∞: | ||
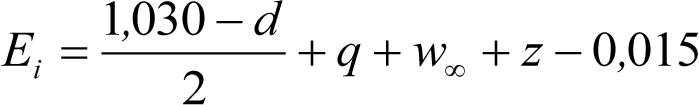
|
||
| Para curva de radio R ≥ 100 m: | ||

|
||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |
| Para curva de radio 80 ≤ R < 100 m: | ||

|
||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |
b) Caso general. Reducción en secciones externas Ea
Para cada punto del vehículo el valor de la reducción Ea que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.

o bien, considerando los distintos salientes Sa para partes altas y bajas:
| Para recta R = ∞: | |||

|
|||
| Para curva de radio R ≥ 100 m: | |||

|
|||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | ||
| Para curva de radio 80 ≤ R < 100 m: | |||

|
|||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | ||
c) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones internas Ei
En este caso: 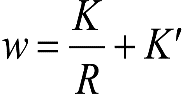 . Las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=100 ó 80 m).
. Las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=100 ó 80 m).
Si: 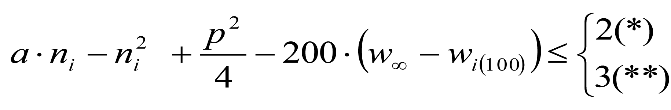 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||

|
||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |
Si:  ⇒ La máx. reducción se da en curva (R=100 ó 80 m) ⇒ La máx. reducción se da en curva (R=100 ó 80 m) |
||
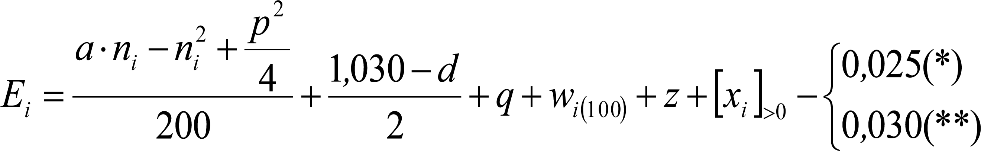
|
||
|
siendo xi un factor para pasar de R=100 a 80 m, de valor:
|
||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |
d) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones externas Ea
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||

|
||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | |
Si:  ⇒ La máx. reducción se da en curva (R=100 ó 80 m) ⇒ La máx. reducción se da en curva (R=100 ó 80 m) |
||
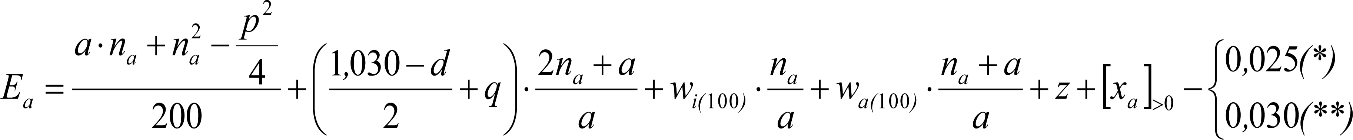
|
||
|
siendo xa un factor para pasar de R=100 a 80 m, de valor:
|
||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | |
2.9.3.1.2 Material remolcado montado sobre bogies
Se consideran indistintamente dos bogies portadores o cuasiportadores.
a) Caso general. Reducción en secciones internas Ei
Para cada punto del vehículo el valor de la reducción Ei que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.

o bien, considerando los distintos salientes Si para partes altas y bajas:
| Para recta R = ∞: | |
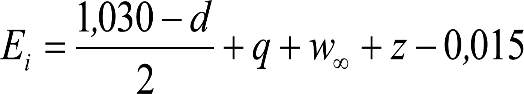
|
|
| Para curva de radio R ≥ 100 m: | |
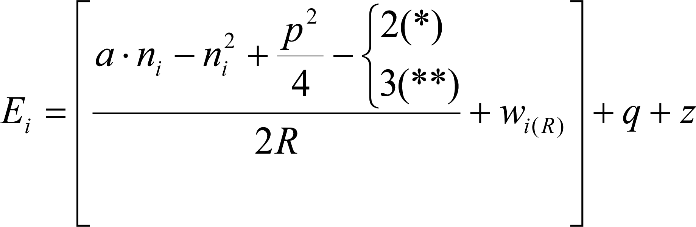
|
|
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
| Para curva de radio 80 ≤ R < 100 m: | |
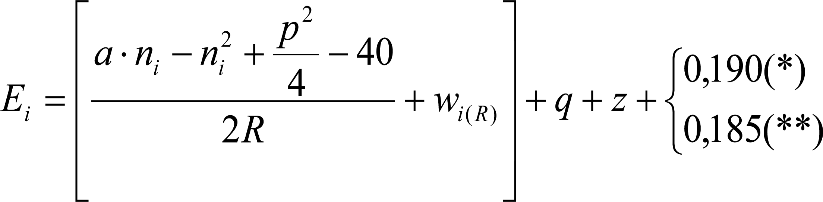
|
|
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
b) Caso general. Reducción en secciones externas Ea
Para cada punto del vehículo el valor de la reducción Ea que se considerará es el mayor de los que resulten de la aplicación de las fórmulas en los cuales el valor de R que se empleará es el que hace máxima la parte entre corchetes.
La reducción considerando los distintos salientes Sa para partes altas y bajas será:

| Para recta R = ∞: |
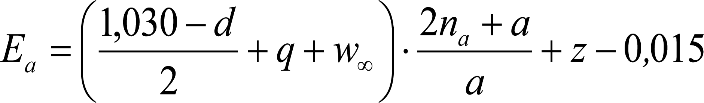
|
| Para curva de radio R ≥ 100 m: | |

|
|
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) |
| Para curva de radio 80 ≤ R < 100 m: | |
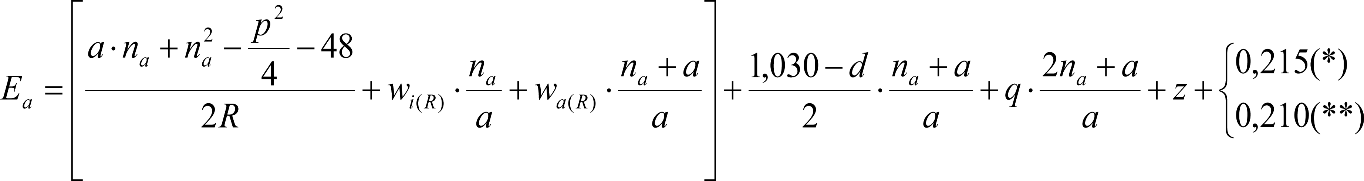
|
|
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) |
c) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones internas Ei
En este caso: 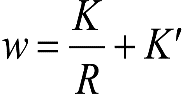 , y las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=100 ó 80 m).
, y las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=100 ó 80 m).
Si: 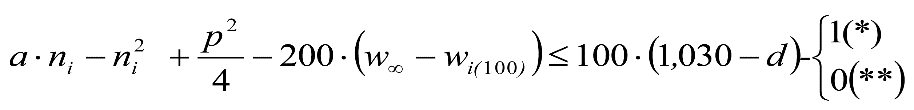 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||
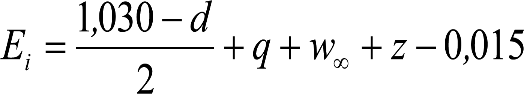
|
||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |
|
Si: |
||
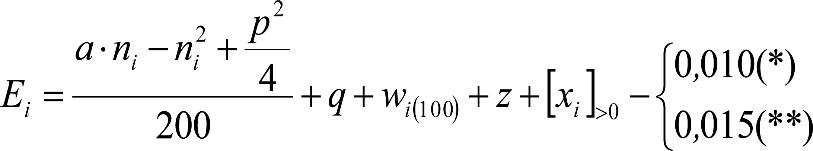
|
||
|
siendo xi un factor para pasar de R=100 a 80 m, de valor:
|
||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |
d) Caso particular de holguras constantes o variables linealmente con la curvatura. Secciones externas Ea
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
|

|
|
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) |
Si: 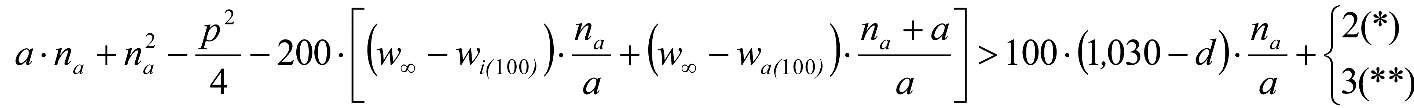 ⇒ La máx. reducción se da en curva (R=100 ó 80 m) ⇒ La máx. reducción se da en curva (R=100 ó 80 m) |
|
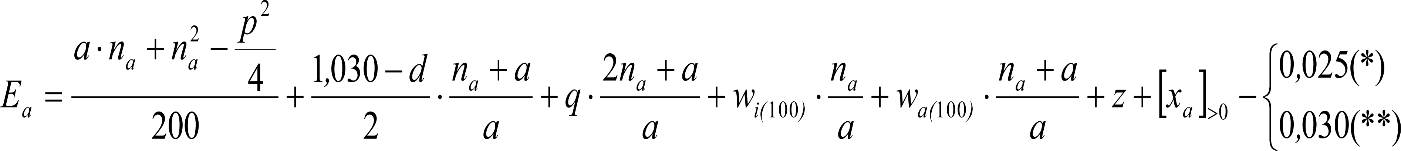
|
|
|
siendo xa un factor para pasar de R=100 a 80 m, de valor:
|
|
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) |
e) Caso particular de vagones con bogies. Secciones internas Ei
En este caso, la holgura es constante, es decir, w∞= wi(R) = wa(R) = w.
Si: 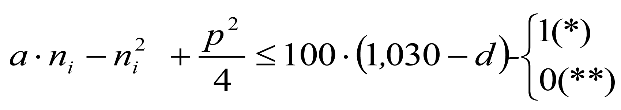 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||

|
||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |
|
Si: |
||
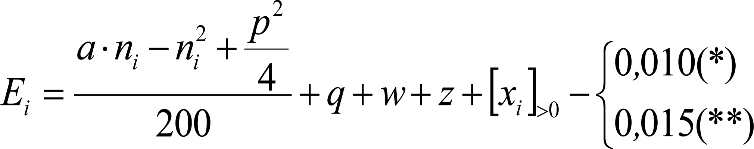
|
||
|
siendo xi un factor para pasar de R=100 a 80 m, de valor:
|
||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |
f) Caso particular de vagones con bogies. Secciones externas Ea
Si: 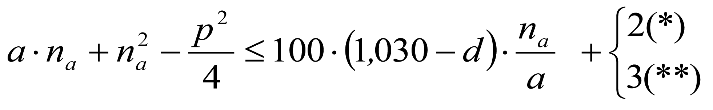 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||

|
||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | |
Si: 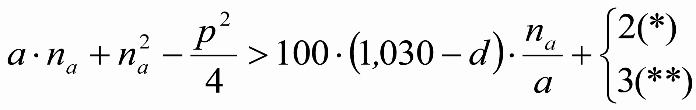 ⇒ La máx. reducción se da en curva (R=100 ó 80 m) ⇒ La máx. reducción se da en curva (R=100 ó 80 m) |
||
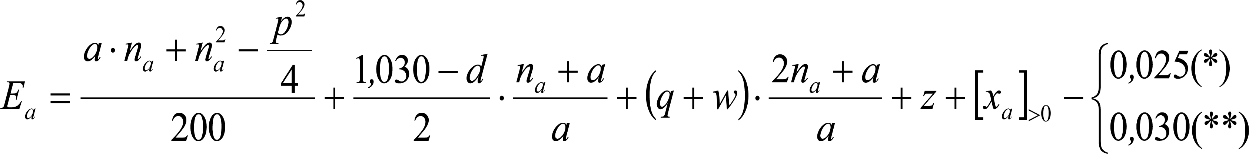
|
||
|
siendo xa un factor para pasar de R=100 a 80 m, de valor:
|
||
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) | |
2.9.3.1.3 Vagones sin bogies
Las reducciones se obtendrán particularizando las de material motor, con p=0 y w∞= wi(R)= wa(R) = w= 0 (al no existir bogies).
a) Reducción en secciones internas Ei
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||

|
||
Si:  ⇒ La máx. reducción se da en curva (R=100 ó 80 m) ⇒ La máx. reducción se da en curva (R=100 ó 80 m) |
||
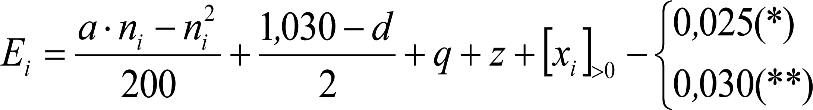
|
||
|
siendo xi un factor para pasar de R=100 a 80 m, de valor:
|
||
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) | |
b) Reducción en secciones externas Ea
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
|
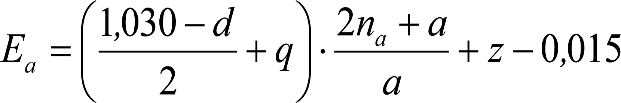
|
|
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) |
Si: 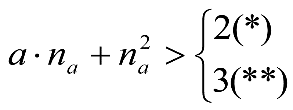 ⇒ La máx. reducción se da en curva (R=100 ó 80 m) ⇒ La máx. reducción se da en curva (R=100 ó 80 m) |
|

|
|
|
siendo xa un factor para pasar de R=100 a 80 m, de valor:
|
|
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) |
2.9.3.1.4 Vehículos autopropulsados
Se utilizarán las fórmulas de reducción del cuadro 2.19, en función del coeficiente de adherencia rueda-carril (μ).
| Tipo de bogies | Valor de μ de cada bogie | Posición de rodadura sobre la vía | Fórmulas de reducción definidas en apartado |
|---|---|---|---|
| Dos bogies motores | μ ≥ 0,2 | Casos 2 y 5 del cuadro 2.4 | 2.9.3.1.1 |
| Dos bogies cuasi-portadores | 0 <μ < 0,2 | Casos 2 y 7 del cuadro 2.4 | 2.9.3.1.2 |
| Un bogie cuasi-portador y otro portador |
0 <μ < 0,2 μ = 0,2 |
||
| Dos bogies portadores | μ = 0,2 | ||
| Un bogie motor y otro portador |
μ ≥ 0,2 μ = 0,2 |
Casos 3 y 6 del cuadro 2.4 |
2.9.3.1.41 2.9.3.1.11 |
| Un bogie motor y otro cuasi-portador |
μ ≥ 0,2 0 <μ < 0,2 |
||
| Los valores obtenidos de las fórmulas de reducción para vehículos motores y autopropulsados son parecidos. En general se utilizan las de vehículos motores, reservando las fórmulas de autopropulsados para aquellos casos en que la menor reducción obtenida sea significativa (0 a 12,5 mm según la sección considerada del vehículo), lo cual ocurre en el centro y extremos de la caja. | |||
|
Cuadro 2.19. Fórmulas de reducción aplicables a los vehículos autopropulsados |
|||
La potencia de los vehículos autopropulsados es generalmente inferior a la de las locomotoras. Al existir un bogie motor y otro portador, sus características serán diferentes.
Se denomina:
p, w∞, wi, wa: empate y holguras del bogie motor.
p’, w’∞, w’i, w’a: empate y holguras del bogie portador.
nμ: distancia desde la sección interior considerada, hasta el pivote del bogie motor.
a) Reducción en secciones internas Ei
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
a.1) En recta:

o bien, considerando el saliente Si:
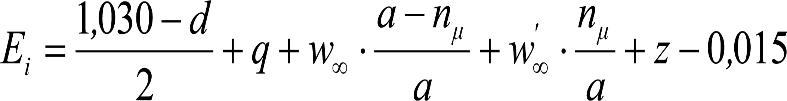
a.2) En curva:

o bien, considerando los distintos salientes Si:
| Para curvas de radio R=100 ó 80 m: | |
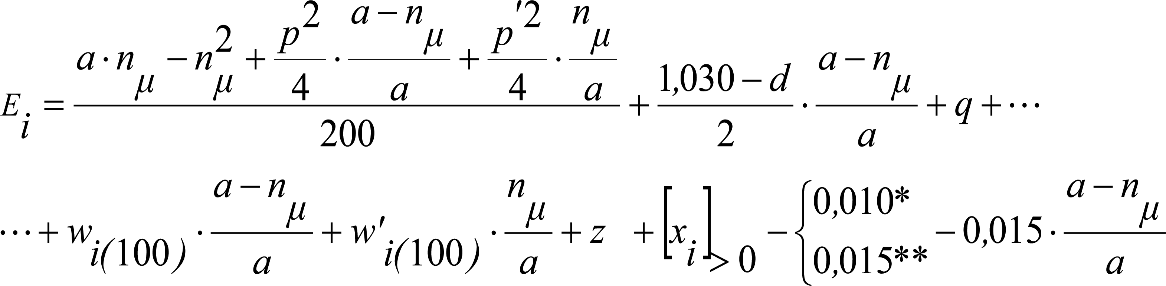
|
|
|
siendo xi un factor para pasar de R=100 a 800 m, de valor:
|
|
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
b) Reducción en secciones externas lado bogie motor Ea
En este caso el bogie motor va delante del bogie portador en el sentido de la marcha.
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
b.1) En recta:
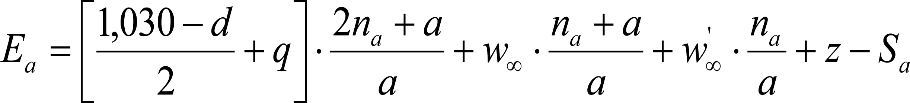
o bien, considerando el saliente Sa:
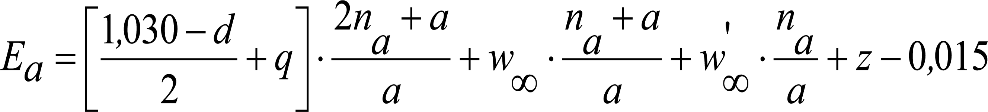
b.2) En curva:
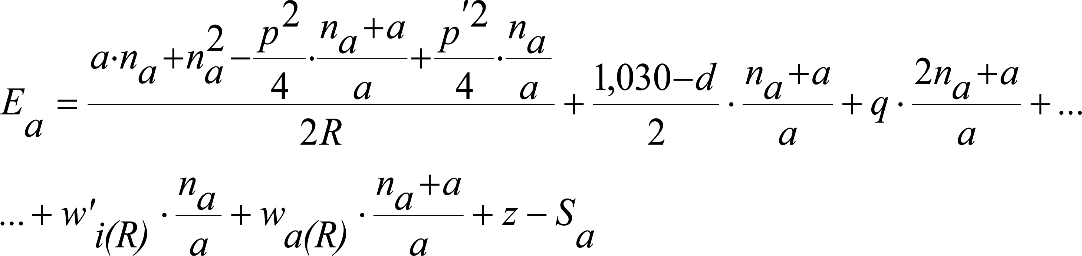
o bien, considerando los distintos salientes Sa:
| Para curvas de radio R=100 ó 80 m: | |

|
|
|
siendo xa un factor para pasar de R=100 a 80 m, de valor:
|
|
| (*) valor a aplicar en Ea de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en Ea de partes altas (h > 0,400 m) |
c) Reducción en secciones externas lado bogie portador Ea
En este caso el bogie portador va delante del bogie motor en el sentido de la marcha.
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
c.1) En recta:
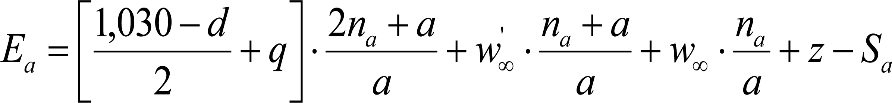
o bien, considerando el saliente Sa:
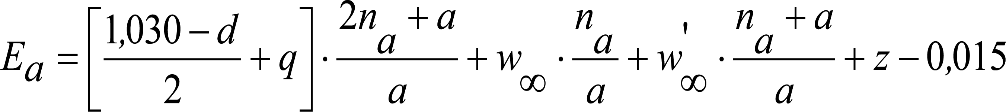
c.2) En curva:

o bien, considerando los distintos salientes Sa:
| Para curvas de radio R=100 ó 80: | |
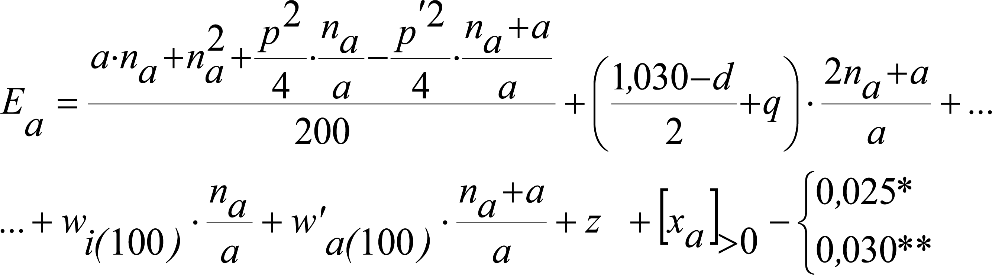
|
|
|
siendo xa un factor para pasar de R=100 a 80 m, de valor:
|
|
| (*) valor a aplicar en E a de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E a de partes altas (h > 0,400 m) |
2.9.4 CÁLCULO DEL GÁLIBO DEL PANTÓGRAFO EN POSICIÓN DE CAPTACIÓN
Los parámetros considerados para el cálculo del gálibo del pantógrafo serán:
– lN = 1,000 m.
– L = 1,055 m.
– D’o = I’o = 0,070 m
– Dmáx = Imáx = 0,120 m.
– s’o = 0,225.
– h’co = 0,5 m.
– Salientes del vehículo real: 
Siendo: ![]() y
y 
– Altura máxima de verificación del gálibo: h’o = 5,5 m.
– Altura mínima de verificación del gálibo: h’u = 4,3 m.
– Desplazamientos laterales máximos del vehículo tipo con pantógrafo, a ambos lados de su posición media, para las dos alturas de verificación:
– Para la altura máxima h’o: e*po = 0,130 m.
– Para la altura mínima h’u: e*pu = 0,082 m.
– Para una altura intermedia h: 
Con el pantógrafo en posición de captación, se considerarán dos casos:
∙ Caso general: Vehículo con holguras no variables linealmente con la curvatura. Se analizarán las situaciones de vehículo en recta R = ∞ y en curvas de R = 80 m y de otros R en los que la variación de w presente alguna discontinuidad.
∙ Caso particular: Vehículo con holgura variable linealmente con la curvatura 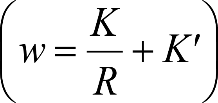 . Se analizarán las situaciones de vehículo en recta R = ∞ y en curva de R = 80 m.
. Se analizarán las situaciones de vehículo en recta R = ∞ y en curva de R = 80 m.
2.9.4.1 Vehículos convencionales
2.9.4.1.1 Secciones internas
Se considera la situación de vehículo parado en vía peraltada.
a) Para s ≤ 0,225
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=5,5m):

Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=4,3m):
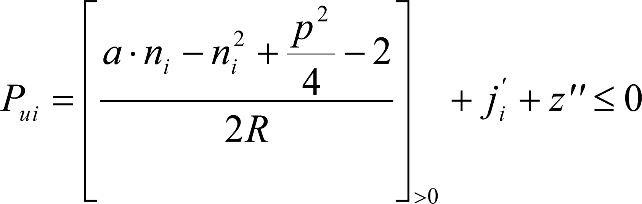
siendo:
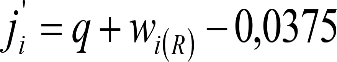


b) Para s > 0,225
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=5,5m):

Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=4,3m):

siendo:
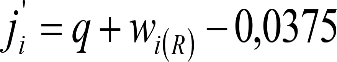
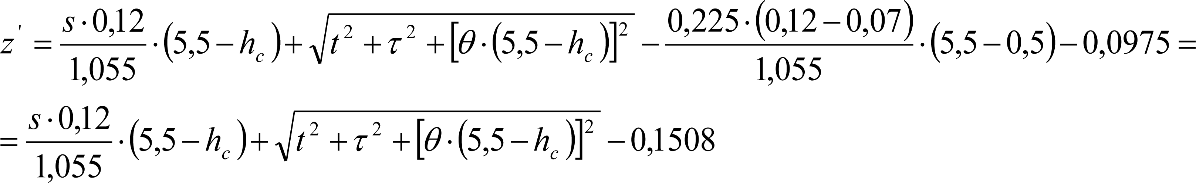
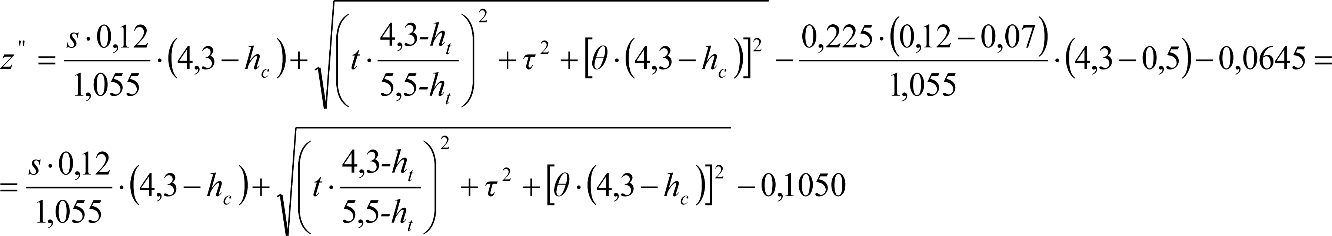
2.9.4.1.2 Secciones externas
Se considera la situación de vehículo circulando con insuficiencia de peralte.
a) Para s ≤ 0,225
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=5,5m):
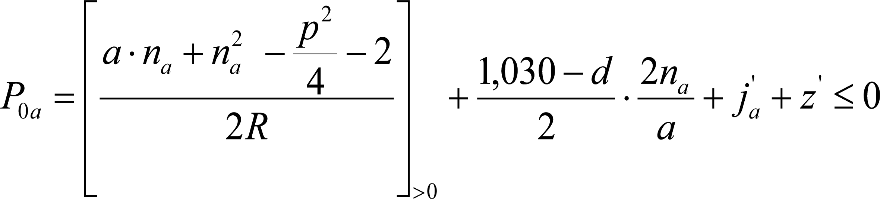
Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=4,3m):

siendo:
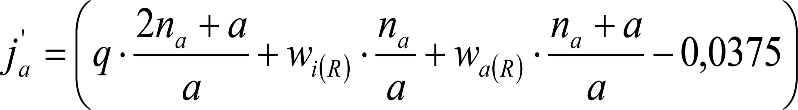

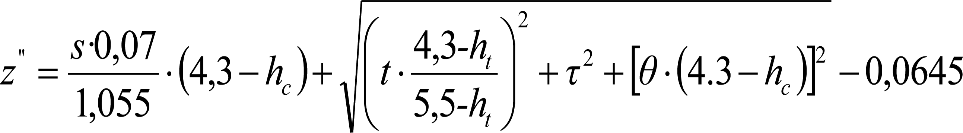
b) Para s > 0,225
Para que el pantógrafo permanezca dentro del gálibo, en su punto más alto de captación (h’o=5,5m):
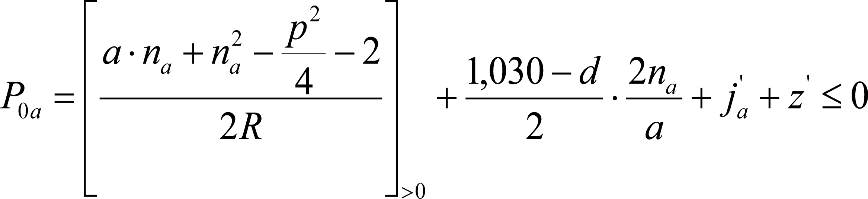
Para que el pantógrafo permanezca dentro del gálibo, en su punto más bajo de captación (h’u=4,3m):
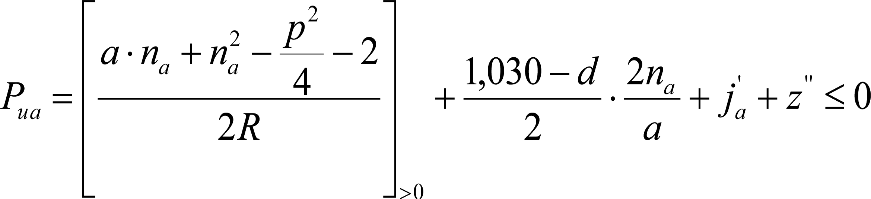
siendo:
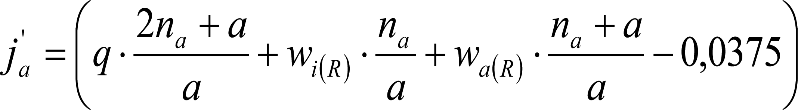
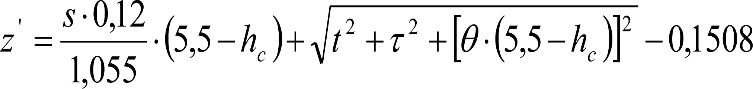
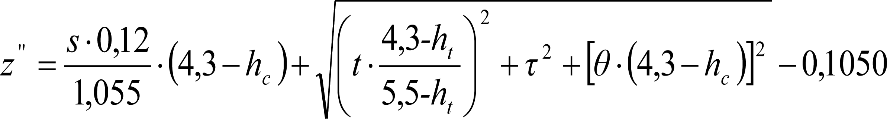
3.1 GÁLIBOS DE IMPLANTACIÓN DE OBSTÁCULOS
Según la norma EN 15273-3:2013(1), el gálibo de implantación de obstáculos es el espacio en torno a la vía, que no debe ser invadido por obstáculos, ni por vehículos que circulen por las vías adyacentes, al objeto de preservar la seguridad en la explotación.
(1) EN 15273-3:2013. Aplicaciones ferroviarias. Gálibos. Parte 3: Gálibo de implantación de obstáculos.
Se obtendrá a partir de los contornos de referencia del gálibo cinemático definidos en los apartados 2.7.1, 2.8.1 y 2.9.1 y de las reglas asociadas del apartado 3.2.
Se consideran tres tipos de gálibo de implantación obstáculos:
a) Gálibo límite
Se define para un punto o tramo de línea. Delimita el espacio que no debe invadir ningún obstáculo en circunstancia alguna, a fin de permitir la circulación normal de los vehículos, más una reserva para considerar las variaciones tolerables de la posición de la vía que se producen entre dos operaciones normales de mantenimiento. Este gálibo se utiliza, por ejemplo, para comprobar si es posible el paso de transportes excepcionales por un determinado punto.
b) Gálibo nominal
Se define para un punto o tramo de línea. Es similar al gálibo límite, pero incorporando unos márgenes complementarios para la circulación de transportes excepcionales, incrementos de velocidad, etc.
c) Gálibo uniforme
Se define para una línea. Es un gálibo nominal obtenido para una envolvente de parámetros (radios, peraltes, etc.) suficientemente desfavorables, que no se superan en la mayor parte de la línea. De esta forma se puede utilizar un único gálibo para toda ella, comprobando que no se superan los parámetros de partida.
Se define a partir de los contornos de referencia de los gálibos cinemáticos: GEB16, GEC16, GB, GC, GEE10 y GED10. No se considera el del gálibo GEA16, pues se asimila al que se obtiene del GEB16(2).
(2) La unificación de los gálibos de implantación de obstáculos GEA16 y GEB16 se debe a que la anchura de sus contornos de referencia difiere únicamente en el intervalo de alturas (4350,3700 mm), donde el GEB16 es ligeramente más ancho (1360-1250=110 mm). Ello podría dar problemas a los vehículos GEB16 que circulen por líneas existentes tipo GEA16 (consideradas GEB16), ya que esta reducción de espacio se da en una zona que puede ser crítica (p.ej. en túneles). Sin embargo, dicha diferencia (110 mm) queda cubierta por los márgenes (200 mm) que incorpora el gálibo nominal.
3.2 REGLAS ASOCIADAS
Consisten en un conjunto de ampliaciones a aplicar al contorno de referencia, con el fin de definir la distancia mínima de ubicación de obstáculos, teniendo en cuenta posibles desplazamientos del vehículo respecto a su posición teórica, debidos a: el trazado (radio de curva, peralte, acuerdos verticales), la velocidad de la línea (insuficiencia de peralte), efectos de la suspensión, posibles desplazamientos aleatorios de la vía y ciertos márgenes complementarios para circulación de transportes excepcionales, incrementos de velocidad, etc.
3.2.1 AMPLIACIONES A CONSIDERAR
1. El semiancho del contorno de referencia, se ampliará con los desplazamientos laterales siguientes:
a) Salientes (Si, Sa).
b) Desplazamientos cuasiestáticos laterales (qs) debidos a exceso o insuficiencia de peralte comprendido entre Do y D, o entre Io e I, para un coeficiente de flexibilidad so.
c) Desplazamientos aleatorios laterales (M1+M2), debidos a:
∙ Desplazamiento de la vía (Tvía).
∙ Desviaciones en el peralte (TD).
∙ Disimetrías del vehículo (ηo).
∙ Oscilaciones del vehículo debidas a irregularidades de la vía (αosc).
d) Márgenes complementarios (M3b).
2. Las cotas verticales del contorno de referencia, se ampliarán en las partes altas o se reducirán en las partes bajas con los desplazamientos debidos a:
a) Inscripción en acuerdos verticales (ΔhRV).
b) Desplazamientos cuasiestáticos perpendiculares al plano de rodadura (ΔhPT) debidos a exceso o insuficiencia de peralte comprendido entre Do y D, o entre Io e I, para un coeficiente de flexibilidad so.
c) Desplazamientos aleatorios perpendiculares al plano de rodadura.
d) Márgenes complementarios (M3h).
3.2.2 DESPLAZAMIENTOS LATERALES
En este apartado se definen los desplazamientos laterales del vehículo a considerar en la ampliación del semiancho del contorno de referencia.
3.2.2.1 Salientes
Se considerarán los salientes Si y Sa definidos en los apartados 2.7.2.4, 2.8.2.4 y 2.9.2.4 en función del ancho de vía y del radio de curva existentes en la sección de vía considerada.
En la zona de ruedas no se considerarán salientes.
3.2.2.2 Desplazamientos cuasiestáticos laterales (solo para h>hco)
Un vehículo circulando por una curva con insuficiencia de peralte (I), o parado en ella (exceso de peralte igual al peralte existente, D), debido a la flexibilidad de la suspensión, gira alrededor de un eje teórico situado a una altura hco sobre el plano de rodadura, lo que produce movimientos laterales de los puntos de su contorno.
Se considerarán los desplazamientos cuasiestáticos laterales, debidos a las diferencias entre los excesos o insuficiencias de peralte reales (D, I), y los considerados en el cálculo del gálibo del material rodante (Do, Io), para un coeficiente de flexibilidad (so):
∙ Vehículo parado (máximo exceso de peralte D), hacia el interior y exterior de la curva:
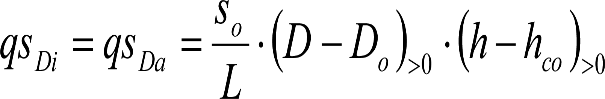
∙ Vehículo circulando a la máxima velocidad permitida (máxima insuficiencia de peralte I), hacia el interior y exterior de la curva:
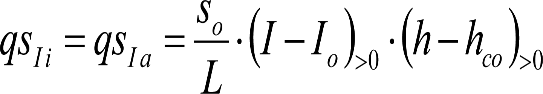
siendo:
h: altura de un punto del contorno del vehículo, medida sobre el plano de rodadura y perpendicularmente a éste, situado entre la altura hco y el techo del mismo. Para h<hco, no se consideran desplazamientos cuasiestáticos laterales.
3.2.2.3 Desplazamientos aleatorios laterales (M1+M2)
a) Por desplazamiento de la vía
Se considerará que entre dos operaciones de mantenimiento periódico, la vía puede desplazarse lateralmente, a cualquier lado de su eje teórico, un valor Tvía.
b) Por desviaciones del peralte
Se considerarán los desplazamientos laterales, geométricos y cuasiestáticos, a una altura h sobre el plano de rodadura, debidos a una desviación del peralte real, por encima o por debajo de su nivel teórico, de valor TD.
– Desplazamiento geométrico: 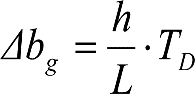
– Desplazamiento cuasiestático: 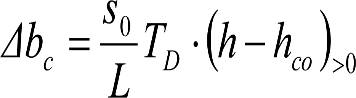
– Desplazamiento total: 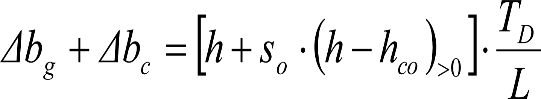
Para h>hco: Δbg y Δbc se desplazan hacia el interior de la curva cuando el peralte real es mayor que el teórico, y hacia el exterior cuando es menor. Para h<hco: Δbg se desplaza al contrario que lo anterior, y Δbc=0.
c)Por disimetrías del vehículo (ηo) (solo para h>hco)
Se considerarán los posibles giros de la caja del vehículo, alrededor de su centro de balanceo, debidos a disimetrías por:
– Tolerancias en el reglaje de la suspensión del vehículo: αsusp
– Reparto desigual de las cargas en el vehículo: αc
En consecuencia, el giro total será: 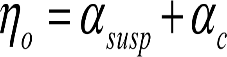
y el desplazamiento lateral, a ambos lados de la posición de equilibrio, para una altura h, será:

d)Por oscilaciones del vehículo debidas a irregularidades de la vía (solo para h>hco)
Las irregularidades de la vía producen oscilaciones del vehículo, que se traducen en giros de la caja (αosc). Su amplitud depende de la calidad de la vía, de las características de la suspensión y de la velocidad del vehículo.
El desplazamiento lateral debido al giro αosc,, a ambos lados de la posición de equilibrio, para una altura h, será:
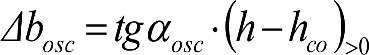
3.2.2.4 Márgenes complementarios laterales (M3b)
Para el cálculo de gálibos nominales de implantación de obstáculos se considerarán unos márgenes laterales complementarios (M3b) para:
∙ Permitir incrementos de velocidad y aumento de la seguridad.
∙ Circulación de transportes excepcionales.
∙ Futuras modificaciones de trazado o de gálibo.
∙ Tener en cuenta los efectos aerodinámicos y vientos transversales.
∙ Facilitar obras en la vía (aparatos de vía, etc.).
Estos márgenes se aplicarán únicamente en las partes altas.
3.2.3.DESPLAZAMIENTOS PERPENDICULARES AL PLANO DE RODADURA
En este apartado se definen los desplazamientos perpendiculares al plano de rodadura a considerar en la ampliación de las partes altas (h>0,4m) y bajas (h≤0,4m) del contorno de referencia.
3.2.3.1.Inscripción en acuerdos verticales
En acuerdos verticales de radio Rv:
a) Partes altas
Las cotas verticales de los puntos del contorno de referencia por encima de la anchura máxima se aumentarán en ![]() y los puntos del contorno de referencia por debajo de la anchura máxima se reducirán en
y los puntos del contorno de referencia por debajo de la anchura máxima se reducirán en ![]() .
.
b) Partes bajas (h≤0,4m)
Las cotas verticales de las partes bajas fuera de la zona de ruedas del contorno de referencia se reducirán en ![]() .
.
En la zona de ruedas no se considerarán desplazamientos por inscripción en acuerdos verticales.
3.2.3.2. Desplazamientos cuasiestáticos perpendiculares al plano de rodadura
a)Partes altas (solo puntos PT)
La rotación de un vehículo debida a los efectos cuasiestáticos causados por D e I, da lugar a movimientos verticales de los puntos de su contorno. Para un punto alto PT, situado a una altura hPT respecto al plano de rodadura y a una distancia horizontal bPT respecto al eje de la vía, el desplazamiento vertical será:
∙ Vehículo parado con peralte D:
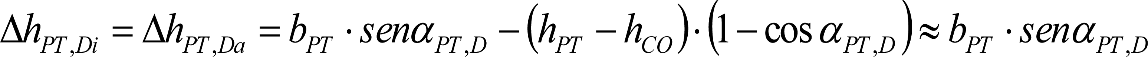
(descenso en el lado interior de la curva y elevación en el exterior)
∙ Vehículo circulando con insuficiencia de peralte I:

(elevación en el lado interior de la curva y descenso en el exterior)
siendo:
αPT,D, αPT,I: Máxima rotación cuasiestática del vehículo hacia el interior y el exterior, respectivamente. Por tanto: 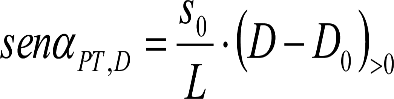 y
y 
hPT, bPT: Coordenadas de los puntos laterales extremos de la línea superior horizontal del contorno de referencia (PT).
hco: Altura del centro de balanceo (Co) del vehículo respecto al plano de rodadura, adoptado por convenio entre material rodante e infraestructura.
|
Figura 3.1. Efecto de la rotación del vehículo |
b)Partes bajas (h≤0,4m)
El fenómeno es análogo al de las partes altas, si bien es tenido en cuenta por el material rodante.
3.2.3.3 Desplazamientos aleatorios perpendiculares al plano de rodadura
a) Desplazamiento vertical de la vía
Se considerará que entre dos operaciones de mantenimiento periódico, la vía puede desplazarse verticalmente, por encima o por debajo de su nivel teórico, un valor TN.
Para las partes bajas entre carriles y para aquellos obstáculos que se muevan solidariamente con la vía el desplazamiento vertical será el correspondiente al desgaste de los carriles.
b)Por desviaciones del peralte (solo puntos PT)
Análogamente al apartado 3.2.2.3, se considerarán los desplazamientos verticales geométricos y cuasiestáticos a una distancia bPT del eje de la vía, debidos a una desviación del peralte real, por encima o por debajo de su nivel teórico, de valor TD.
– Desplazamiento geométrico (de elevación o descenso) en el lado exterior de la curva (hilo alto): 
– Desplazamiento geométrico (de elevación o descenso) en el lado interior de la curva (hilo bajo): 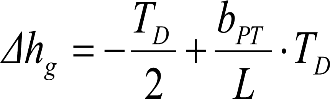
– Desplazamiento cuasiestático adicional: 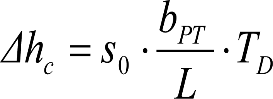
– Desplazamiento total:
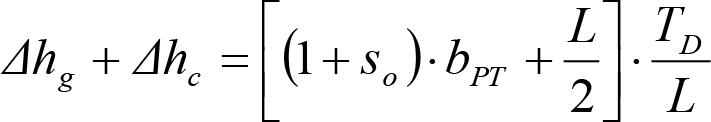 (lado exterior de la curva)
(lado exterior de la curva)
 (lado interior de la curva)
(lado interior de la curva)
c)Por disimetrías del vehículo (ηo) (solo puntos PT)
Análogamente al apartado 3.2.2.3, se considerarán los giros producidos por disimetrías del vehículo, alrededor de su centro de balanceo, debidas a:
– Tolerancias en el reglaje de la suspensión del vehículo: αsusp.
– Reparto desigual de las cargas en el vehículo: αc.
El desplazamiento vertical (elevación o descenso) a una distancia bPT será:

d)Por oscilaciones del vehículo debidas a irregularidades de la vía (solo puntos PT)
Análogamente al apartado 3.2.2.3, el desplazamiento vertical (elevación o descenso) debido al giro αosc, será:

3.2.3.4 Márgenes complementarios perpendiculares al plano de rodadura (M3h)
Para el caso de gálibos nominales se considerarán unos márgenes complementarios en sentido perpendicular al plano de rodadura (M3h), análogos a los del apartado 3.2.2.4.
Estos márgenes se aplicarán únicamente en las partes altas.
3.2.3.5 Margen perpendicular al plano de rodadura en la zona de ruedas
En la zona de ruedas con el fin de no dificultar el paso de la pestaña (por ejemplo entarimados de pasos a nivel, de pasos entre vías, etc), deberá tenerse en cuenta un margen a fin de considerar el desgaste del carril.
3.3 GÁLIBO LÍMITE DE IMPLANTACIÓN DE OBSTÁCULOS
Debido a la escasa probabilidad de concurrencia simultánea de todos los desplazamientos aleatorios, se contabilizarán con un valor igual a K veces su media cuadrática.
Se considerarán las dos situaciones siguientes:
a) Vehículo circulando a la máxima velocidad permitida (máxima insuficiencia de peralte I).
b) Vehículo parado (máximo exceso de peralte D).
Para cada una de ellas, se consideran dos casos:
∙ Máximo desplazamiento lateral junto con su desplazamiento máximo compatible perpendicular al plano de rodadura; en lados interior y exterior de la curva.
∙ Máximo desplazamiento perpendicular al plano de rodadura junto con su desplazamiento máximo lateral compatible; en lados interior y exterior de la curva.
En el caso de insuficiencia de peralte, I, los puntos del exterior de la curva situados por encima de hco se desplazan lateralmente hacia el exterior y verticalmente hacia abajo, mientras que los del interior de la curva se desplazan hacia el exterior de ella y hacia arriba. Del mismo modo, en el caso de vehículo parado (exceso de peralte D), los puntos del exterior de la curva situados por encima de hco se desplazan hacia el interior de la curva y hacia arriba, mientras que los puntos del interior de la curva se moverán hacia el interior de la misma y hacia abajo.
Los puntos situados por debajo de hco tendrán desplazamientos verticales análogos a los indicados anteriormente. Por el contrario, los desplazamientos laterales irán en sentido contrario.
Los efectos aleatorios (desviaciones del peralte, irregularidades de vía y disimetría) se considerarán con el sentido más desfavorable en cada caso, según se pretenda obtener el máximo movimiento lateral o el máximo movimiento vertical. En cualquier caso su tratamiento deberá ser concordante, es decir, considerando el mismo sentido para el movimiento horizontal y vertical. Para el término TN lo más desfavorable, en general, será considerarlo como elevación en el análisis de los puntos por encima de la anchura máxima del contorno de referencia y de descenso en los puntos por debajo de la anchura máxima del contorno de referencia.
En la figura 3.2 Se indican los puntos a considerar en la definición del gálibo de implantación de obstáculos.
|
1) Plano de rodadura Figura 3.2. Puntos a considerar en la definición del gálibo de implantación de obstáculos |
Para los puntos bajos (h ≤ 0,4 m), tanto en el lado interior como en el exterior de la curva, se considerará el desplazamiento TN debido al desgaste de los carriles, a la hora de situar obstáculos que se muevan solidariamente con la vía.
En el anejo 7 se incluye un ejemplo de determinación del gálibo límite de implantación de obstáculos.
Si en algún punto no se puede cumplir el gálibo uniforme de implantación de partes bajas, se cumplirá al menos el gálibo límite de partes bajas.
Para solucionar problemas de gálibo en un punto determinado se podrá optar por:
1. Aumentar el radio de la curva en planta, lo que reduce el saliente y por tanto la distancia de los obstáculos a la vía. Esta medida es poco útil en el caso de R>250m y anchos de vía ibérico o estándar europeo.
2. Desplazar (ripar) lateralmente el eje de la vía (p.ej. en túneles en curva con peralte en los que el eje de la sección del túnel pasa por el eje de la vía).
3. Disminuir el peralte, lo que reducirá la velocidad de circulación en ese punto.
4. Disponer vía en placa, a fin de eliminar los posibles desplazamientos laterales y defectos de nivelación de la vía, así como las interacciones entre vehículo y vía.
En el cuadro 3.1 se indican las fórmulas para determinar la separación lateral y vertical de los obstáculos cuando se encuentran en curva.
| SITUACIÓN | bobstáculo máximo con h obstáculo compatible | ||
|---|---|---|---|
| Lado interior de la curva | Lado exterior de la curva | ||
|
V máx (I) |
Punto PT |
|
|
| Partes altas:puntos por encima de la anchura máxima |
|
|
|
| Partes altas:puntos por debajo de la anchura máxima |
|
|
|
| Partes bajas (h≤0,4m) |
|
|
|
|
V=0 (D) |
Punto PT |
|
|
| Partes altas:puntos por encima de la anchura máxima |
|
|
|
| Partes altas:puntos por debajo de la anchura máxima |
|
|
|
| Partes bajas (h≤0,4m) |
|
|
|
| SITUACIÓN | hobstáculo máximo con b obstáculo compatible | ||
|---|---|---|---|
| Lado interior de la curva | Lado exterior de la curva | ||
|
V máx (I) |
Punto PT |
|
|
| Partes altas:puntos por encima de la anchura máxima |
|
|
|
| Partes altas:puntos por debajo de la anchura máxima |
|
|
|
| Partes bajas (h≤0,4m) |
|
|
|
|
V=0 (D) |
Punto PT |
|
|
| Partes altas:puntos por encima de la anchura máxima |
|
|
|
| Partes altas:puntos por debajo de la anchura máxima |
|
|
|
| Partes bajas (h≤0,4m) |
|
|
|
|
NOTA: Las casillas sombreadas corresponden a las situaciones generalmente más desfavorables. |
|||
|
Cuadro 3.1. Fórmulas para determinar la separación lateral y vertical de los obstáculos. Curva (gálibo límite) |
|||
siendo:
bobstáculo,i, bobstáculoa,a: distancia entre la perpendicular al plano de rodadura en el eje de la vía y el obstáculo, medida en una sección transversal, paralelamente al plano de rodadura y hacia el interior y exterior de la curva, respectivamente.
hobstáculo,i, hobstáculo,a: altura máxima (bajo el contorno de referencia) o mínima (sobre el contorno de referencia) a la que deben situarse los obstáculos, medida sobre el plano de rodadura y perpendicularmente a éste, en el lado interior y exterior de la curva, respectivamente.
bCR: semiancho del contorno de referencia.
Si, Sa: salientes.
qsIi, qsIa: desplazamientos cuasiestáticos laterales por insuficiencia de peralte en el lado interior y exterior de la curva.
qsDi, qsDa: desplazamientos cuasiestáticos laterales por exceso de peralte en el lado interior y exterior de la curva.
∑j1, ∑j2,∑j1*, ∑j2*: suma de los desplazamientos aleatorios laterales:



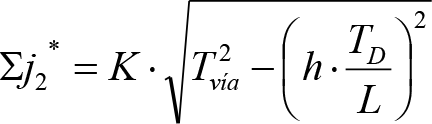
hCR: altura de un punto del contorno de referencia medida perpendicularmente al plano de rodadura.
ΔhRV: desplazamiento vertical debido a la inscripción en acuerdos verticales.
ΔhPTIi, ΔhPTIa: desplazamientos cuasiestáticos verticales de las partes altas por insuficiencia de peralte en el lado interior y exterior de la curva.
ΔhPTDi, ΔhPTDa: desplazamientos cuasiestáticos verticales de las partes altas por exceso de peralte en el lado interior y exterior de la curva
∑Vi, ∑Va: suma de los desplazamientos aleatorios verticales en el interior y exterior de la curva, respectivamente:
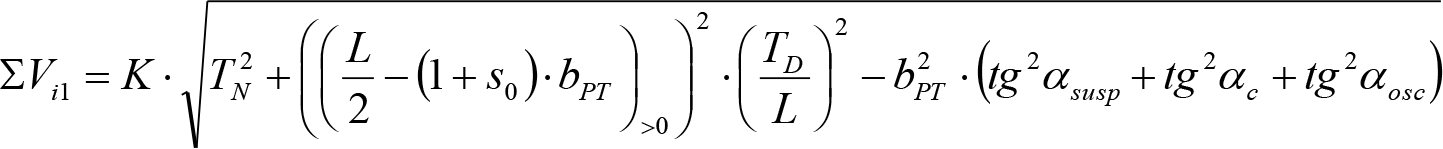
El signo [ ]>0 significa que cuando la expresión entre paréntesis es positiva, mantiene su valor, y cuando es negativa o nula, se toma cero.

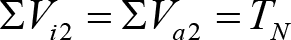

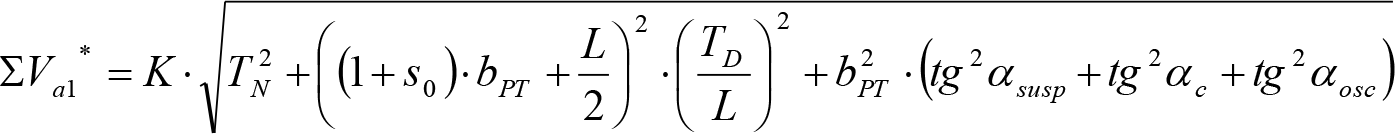
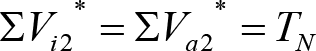
Cuando en alguna de las expresiones 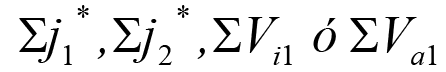 , el radicando sea negativo, quiere decir que el desplazamiento tiene sentido opuesto al considerado inicialmente, por lo que se tomará el valor absoluto del radicando y se cambiará el signo de la expresión.
, el radicando sea negativo, quiere decir que el desplazamiento tiene sentido opuesto al considerado inicialmente, por lo que se tomará el valor absoluto del radicando y se cambiará el signo de la expresión.
En el cuadro 3.2 se indican las fórmulas para determinar la separación lateral y vertical de los obstáculos cuando la vía se encuentra en recta.
En este caso el gálibo es simétrico al realizarse las siguientes consideraciones:
– En el caso del desplazamiento aleatorio αosc se tomará el valor del exterior de la curva tanto para los desplazamientos laterales como verticales.
– El desplazamiento cuasiestático perpendicular al plano de rodadura es cero.
| SITUACIÓN | bobstáculo máximo con h obstáculo compatible | hobstáculo máximo con b obstáculo compatible |
|---|---|---|
| Punto PT |
|
|
| Partes altas:puntos por encima de la anchura máxima |
|
|
| Partes altas:puntos por debajo de la anchura máxima |
|
|
| Partes bajas (h≤0,4m) |
|
|
|
Cuadro 3.2. Fórmulas para determinar la separación lateral y vertical de los obstáculos. Recta (gálibo límite). |
||
siendo:



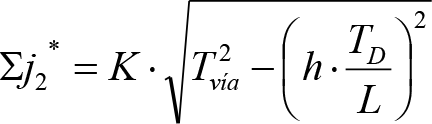

El signo [ ]>0 significa que cuando la expresión entre paréntesis es positiva, mantiene su valor, y cuando es negativa o nula, se toma cero.
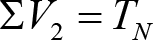
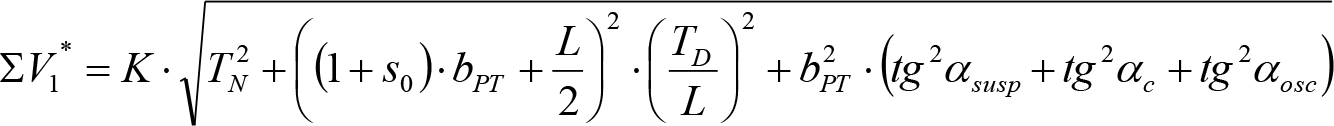
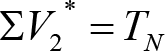
Cuando en alguna de las expresiones 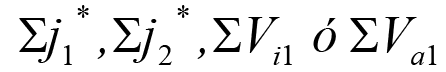 , el radicando sea negativo, quiere decir que el desplazamiento tiene sentido opuesto al considerado inicialmente, por lo que se tomará el valor absoluto del radicando y se cambiará el signo de la expresión.
, el radicando sea negativo, quiere decir que el desplazamiento tiene sentido opuesto al considerado inicialmente, por lo que se tomará el valor absoluto del radicando y se cambiará el signo de la expresión.
3.4 GÁLIBO NOMINAL DE IMPLANTACIÓN DE OBSTÁCULOS
En este caso, debido a la mayor probabilidad de concurrencia simultánea de todos los desplazamientos aleatorios, éstos se sumarán directamente.
Se considerarán las mismas situaciones que para el gálibo límite de implantación de obstáculos, es decir:
a) Vehículo circulando a la máxima velocidad permitida (máxima insuficiencia de peralte I).
b) Vehículo parado (máximo exceso de peralte D).
Y para cada una de ellas, se consideran dos casos:
∙ Máximo desplazamiento lateral junto con su desplazamiento máximo compatible perpendicular al plano de rodadura; en lados interior y exterior de la curva.
∙ Máximo desplazamiento perpendicular al plano de rodadura junto con su desplazamiento máximo lateral compatible; en lados interior y exterior de la curva.
En el cuadro 3.3 se indican las fórmulas para determinar la separación lateral y vertical de los obstáculos cuando se encuentran en curva.
| SITUACIÓN | bobstáculo máximo con h obstáculo compatible | ||
|---|---|---|---|
| Lado interior de la curva | Lado exterior de la curva | ||
|
V máx (I) |
Punto PT |
|
|
| Partes altas:puntos por encima de la anchura máxima |
|
|
|
| Partes altas:puntos por debajo de la anchura máxima |
|
|
|
| Partes bajas (h≤0,4m) |
|
|
|
|
V=0 (D) |
Punto PT |
|
|
| Partes altas:puntos por encima de la anchura máxima |
|
|
|
| Partes altas:puntos por debajo de la anchura máxima |
|
|
|
| Partes bajas (h≤0,4m) |
|
|
|
| SITUACIÓN | hobstáculo máximo con b obstáculo compatible | ||
|---|---|---|---|
| Lado interior de la curva | Lado exterior de la curva | ||
|
V máx (I) |
Punto PT |
|
|
| Partes altas:puntos por encima de la anchura máxima |
|
|
|
| Partes altas:puntos por debajo de la anchura máxima |
|
|
|
| Partes bajas (h≤0,4m) |
|
|
|
|
V=0 (D) |
Punto PT |
|
|
| Partes altas:puntos por encima de la anchura máxima |
|
|
|
| Partes altas:puntos por debajo de la anchura máxima |
|
|
|
| Partes bajas (h≤0,4m) |
|
|
|
|
NOTA: Las casillas sombreadas corresponden a las situaciones generalmente más desfavorables. |
|||
|
Cuadro 3.3. Fórmulas para determinar la separación lateral y vertical de los obstáculos. Curva (gálibo nominal) |
|||
siendo:
bobstáculo,i, bobstáculoa,a: distancia entre la perpendicular al plano de rodadura en el eje de la vía y el obstáculo, medida en una sección transversal, paralelamente al plano de rodadura y hacia el interior y exterior de la curva, respectivamente..
hobstáculo,i, hobstáculo,a: altura máxima (bajo el contorno de referencia) o mínima (sobre el contorno de referencia) a la que deben situarse los obstáculos, medida sobre el plano de rodadura y perpendicularmente a éste, en el lado interior y exterior de la curva, respectivamente.
bCR: semiancho del contorno de referencia.
Si, Sa: salientes.
qsIi, qsIa: desplazamientos cuasiestáticos laterales por insuficiencia de peralte en el lado interior y exterior de la curva.
qsDi, qsDa: desplazamientos cuasiestáticos laterales por exceso de peralte en el lado interior y exterior de la curva.
∑j3, ∑j4,∑j3*, ∑j4*: suma de los desplazamientos aleatorios laterales:
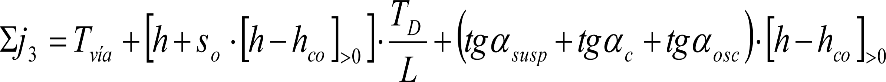


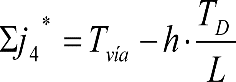
hCR: altura del contorno de referencia.
ΔhRV: desplazamiento vertical debido a la inscripción en acuerdos verticales.
ΔhPTIi, ΔhPTIa: desplazamientos cuasiestáticos verticales de las partes altas por insuficiencia de peralte en el lado interior y exterior de la curva.
ΔhPTDi, ΔhPTDa: desplazamientos cuasiestáticos verticales de las partes altas por exceso de peralte en el lado interior y exterior de la curva
∑Vi, ∑Va: suma de los desplazamientos aleatorios verticales en el interior y exterior de la curva, respectivamente:
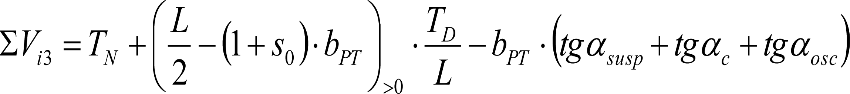

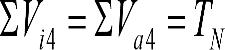

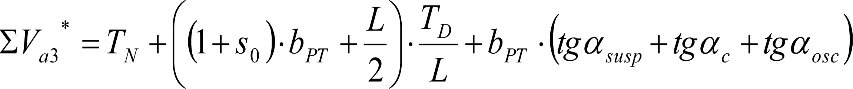
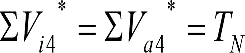
Para los puntos bajos (h ≤ 0,4 m), tanto en el lado interior como en el exterior de la curva, se considerará el desplazamiento TN debido al desgaste de los carriles, a la hora de situar obstáculos que se muevan solidariamente con la vía.
En el anejo 7 se incluye un ejemplo de determinación del gálibo uniforme de implantación de obstáculos, donde se ve la aplicación de las fórmulas del gálibo nominal.
En el cuadro 3.4 se indican las fórmulas para determinar la separación lateral y vertical de los obstáculos cuando la vía se encuentra en recta.
En este caso el gálibo es simétrico al realizarse las siguientes consideraciones:
– En el caso del desplazamiento aleatorio αosc se tomará el valor del exterior de la curva tanto para los desplazamientos laterales como verticales.
– El desplazamiento cuasiestático perpendicular al plano de rodadura es cero.
| SITUACIÓN | bobstáculo máximo con h obstáculo compatible | hobstáculo máximo con b obstáculo compatible |
|---|---|---|
| Punto PT |
|
|
| Partes altas:puntos por encima de la anchura máxima |
|
|
| Partes altas:puntos por debajo de la anchura máxima |
|
|
| Partes bajas (h≤0,4m) |
|
|
|
Cuadro 3.4. Fórmulas para determinar la separación lateral y vertical de los obstáculos. Recta (gálibo nominal). |
||
siendo:
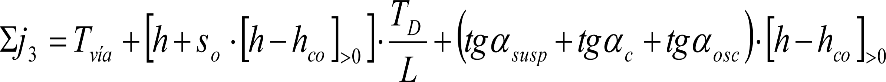


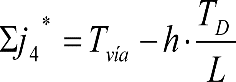

![]()
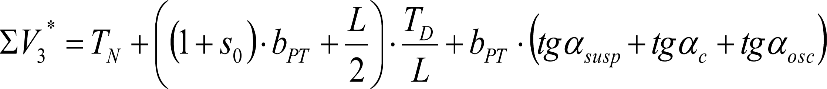
![]()
3.5 GÁLIBO DEL PANTÓGRAFO
Para determinar el gálibo del pantógrafo hay que considerar dos gálibos:
∙ Gálibo mecánico. Tiene en cuenta las interferencias mecánicas.
∙ Gálibo eléctrico. Tiene en cuenta las interferencias eléctricas. Define una distancia de seguridad, por aislamiento, entre la parte del pantógrafo sometida a tensión eléctrica y los obstáculos. Depende de si el pantógrafo dispone o no de trocadores aislados.
La consideración o no del gálibo eléctrico depende de las condiciones de aislamiento o puesta a tierra del obstáculo:
– Los obstáculos que estén a la misma tensión que la línea aérea de contacto no necesitan respetar el gálibo eléctrico. Se situarán en el exterior del gálibo mecánico.
– Los obstáculos aislados tampoco requieren comprobación del gálibo eléctrico. Basta situarlos en el exterior del gálibo mecánico.
– Los obstáculos no aislados (conectados a tierra o a potencial diferente de la línea aérea de contacto) deberán respetar ambos gálibos, situándose en el exterior de los dos.
En la figura 3.3 se muestran los gálibos mecánico y eléctrico del pantógrafo. Se obtendrán a partir del contorno de referencia del pantógrafo definido en los apartados 3.10.4.1, 3.11.4.1 y 3.12.4.1.
|
Figura 3.3. Gálibos mecánico y eléctrico del pantógrafo |
3.5.1 DETERMINACIÓN DEL GÁLIBO MECÁNICO DEL PANTÓGRAFO
En las líneas por las que circule material rodante con pantógrafos de diferente ancho, el gálibo mecánico será el envolvente correspondiente a la mayor anchura y altura obtenidas.
En el anejo 7 se incluye un ejemplo de determinación del gálibo mecánico y eléctrico del pantógrafo.
3.5.1.1 Parámetros que intervienen
Los desplazamientos que intervienen en el cálculo del galibo mecánico del pantógrafo, serán de naturaleza análoga a los considerados en el gálibo límite de implantación de obstáculos.
a)Semiancho de la mesilla del pantógrafo (bw)
Se define en el cuadro 3.5, en función del tipo de pantógrafo.
| Ancho de la mesilla del pantógrafo (mm) | Tensión catenaria | bw (mm) |
|---|---|---|
| 1.700 | 1,5 kV c.c. | 850 |
| 1.950 | 3,0 kV c.c. | 975 |
| 1.950 | 25 kV c.a. | 975 |
| 1.600 | 25 kV c.a. | 800 |
|
Cuadro 3.5. Semiancho de la mesilla del pantógrafo |
||
Nota: No se considera el ancho de mesilla de 1.600 mm en líneas de 3,0 kV por su incompatibilidad con las características de diseño de la catenaria.
b)Desplazamiento lateral del pantógrafo (ep)
Se considerarán los desplazamientos laterales máximos del pantógrafo a ambos lados de su posición de equilibrio, obtenidos a partir de los definidos en el apartado 2.5, siguientes:
∙  en la máxima altura de verificación h’0
en la máxima altura de verificación h’0
∙ ![]() en la mínima altura de verificación h’u
en la mínima altura de verificación h’u
c) Salientes
Tanto en el interior como en el exterior de las curvas, se considerarán los salientes definidos en los apartados 2.7.5, 2.8.5 y 2.9.4.
d) Desplazamientos cuasiestáticos
Se considerarán los desplazamientos del pantógrafo, debidos al balanceo del vehículo motor, siguientes:
 y
y 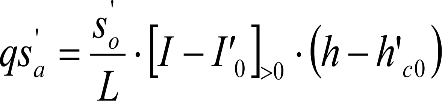
e) Desplazamientos aleatorios laterales
En este apartado se incluyen los siguientes:
∙ Desplazamientos laterales de la vía entre dos operaciones sucesivas de mantenimiento periódico (Tvía).
∙ Desplazamientos geométricos y cuasiestáticos debidos a una desviación (TD) del peralte real respecto al teórico, entre dos operaciones sucesivas de mantenimiento periódico.
∙ Disimetrías del vehículo causadas por reparto asimétrico de las cargas (αc) o tolerancias en el reglaje de la suspensión (αsusp).
∙ Oscilaciones del vehículo generadas por irregularidades de la vía (αosc).
3.5.1.2 Anchura del gálibo mecánico
Se obtendrá a partir de los desplazamientos del apartado 3.5.1.1.
Para los desplazamientos aleatorios, teniendo en cuenta la escasa probabilidad de que ocurran simultáneamente, se considerará un valor igual a K’ veces la media cuadrática de los mismos.
En posición de captación, el pantógrafo estará en contacto permanente con el hilo de contacto, por lo que su altura variará continuamente con la de este último. En consecuencia, el gálibo se estudiará para el intervalo de alturas siguiente:
∙ Altura máxima de verificación: h’0
∙ Altura mínima de verificación: h’u
Entre ambas alturas, la variación del contorno de referencia del pantógrafo será lineal.
Los parámetros que intervienen se definen en la figura 3.4.
|
Figura 3.4. Gálibo de paso libre del pantógrafo |
Los obstáculos deberán situarse a una distancia horizontal mínima respecto al eje del pantógrafo de valor:
∙ Lado interior de la curva: 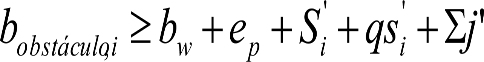
∙ Lado exterior de la curva: 
siendo:
bw: semiancho de la mesilla del pantógrafo.
ep: desplazamiento horizontal del pantógrafo a la altura h. Para h’0 toma el valor epo, y para h’u toma el valor epu.
S’i, S’a: salientes del pantógrafo.
qs’i, qs’a: desplazamientos cuasiestáticos.
∑j’: suma de los márgenes que cubren los desplazamientos aleatorios laterales:

La comprobación se realizará para las alturas máxima y mínima de verificación, interpolando para alturas intermedias.
3.5.1.3 Altura del gálibo mecánico
En posición de captación, el pantógrafo está en contacto permanente con el hilo de contacto, por lo que su altura respecto al plano de rodadura será variable. Se determinará mediante la fórmula:

siendo:
hf: altura del hilo de contacto.
fs: elevación del hilo de contacto debido a la fuerza ascendente (F) transmitida por el pantógrafo en el contacto.
fws: elevación del arco del pantógrafo por encima del plano de contacto debido a la flexibilidad del pantógrafo.
fwa: elevación del arco del pantógrafo por encima del plano de contacto debido al desgaste de la pletina o frotador.
|
(1) Eje del vehículo (2) Hilo de contacto Figura 3.5. Elevación del arco del pantógrafo por encima del plano de contacto |
Los valores de fs yfws+fwa, para diferentes tipos de catenaria se definen en el cuadro 3.6. Se resaltan los valores más desfavorables para V=Vmax y para V=0.
En el caso de catenaria rígida y a falta de información específica se podrán adoptar los siguientes valores de fs yfws+fwa.
fs = 15 mm
fws+fwa = 70 mm
| Tipo de catenaria | Vmax (km/h) | Elasticidad de la catenaria (mm/N) | Fuerzas de contacto entre Pantógrafo y Catenaria (F) | Elevación del hilo de contacto fs (mm), en función de F y V | fws+ fwa (mm) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (para Fm y Vmax) | (Fm+3σmax y Vmax) | (Fmax y Vmax) | (para V=0) | ||||||||||||||||
| Centro vano | Apoyo | Fm (N) | Fm+3σmax (N) | Fmax (N) | Fest (N) | Centro vano | Apoyo | Centro vano | Apoyo | Centro vano | Apoyo | Centro vano | Apoyo | ||||||
| V≤200 | V>200 | ||||||||||||||||||
| CA-160 | 160 | 0,65 | 0,32 | 135 | 256,5 | 300 | ---- | 120 | 88 | 44 | 167 | 83 | 195 | 96 | 78 | 39 | 70 | ||
| CAU-220 | 220 | 0,38 | 0,19 | 157 | 298,3 | 300 | 400 | 120 | 60 | 30 | 114 | 57 | 152 | 76 | 46 | 23 | 70 | ||
| CA-220 | 220 | 0,37 | 0,25 | 157 | 298,3 | 300 | 400 | 120 | 59 | 40 | 111 | 75 | 148 | 100 | 45 | 30 | 70 | ||
| Tipo de catenaria | Vmax (km/h) | Elasticidad catenaria (mm/N) | Fuerzas contacto Pantógrafo-Catenaria (F) | Elevación del hilo de contacto fs (mm), en función de F y V | fws+ fwa (mm) | ||||||||||||||
| (para Fm y Vmax) | (Fm+3σmax y Vmax) | (Fmax y Vmax) | (para V=0) | ||||||||||||||||
| Centro vano | Apoyo | Fm (N) | Fm+3σmax (N) | Fmax (N) | Fest (N) | Centro vano | Apoyo | Centro vano | Apoyo | Centro vano | Apoyo | Centro vano | Apoyo | ||||||
| V≤200 | V>200 | ||||||||||||||||||
| SICAT H 1.0 | 330 | 0,44 | 0,40 | 176 | 334,4 | 300 | 350 | 90 | 78 | 71 | 148 | 134 | 154 | 140 | 40 | 36 | 70 | ||
| EAC-350 | 350 | 0,45 | 0,38 | 189 | 359,1 | 300 | 350 | 90 | 86 | 72 | 162 | 137 | 158 | 133 | 41 | 35 | 70 | ||
|
Cuadro 3.6. Valores de fs y fws+fwa |
|||||||||||||||||||
3.5.2 DETERMINACIÓN DEL GÁLIBO ELÉCTRICO DEL PANTÓGRAFO
En las líneas por las que circule material rodante con pantógrafos de diferente ancho, el gálibo eléctrico será el envolvente correspondiente a la mayor anchura y altura obtenidas.
Se considerarán únicamente las partes no aisladas del pantógrafo. Por tanto, no se tiene en cuenta el trocador aislado.
Dicho gálibo (figura 3.4) se obtendrá a partir del gálibo mecánico, añadiendo la distancia de aislamiento eléctrico (belec) definida en el cuadro 3.7, y restando la anchura (proyección horizontal) del trocador aislado (cw).
| Tensión catenaria | Distancia de aislamiento eléctrico (b elec)(3) | |
|---|---|---|
| Estática (mm) | Dinámica (mm) | |
| 1,5 kV c.c. | 100 | 50 |
| 3,0 kV c.c. | 150 | 50 |
| 25 kV c.a. | 270 | 150 |
|
Cuadro 3.7. Distancias de aislamiento eléctrico |
||
(3) Distancias definidas en la norma UNE-EN 50119:2.010
3.5.2.1 Anchura del gálibo eléctrico
Se obtendrá añadiendo al gálibo mecánico la distancia de aislamiento belec y restándole el valor de cw.
Los obstáculos deberán situarse a una distancia horizontal mínima respecto al eje del pantógrafo de valor:
∙ Lado interior de la curva: 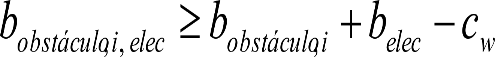
siendo belec la distancia de aislamiento eléctrico estática del cuadro 3.7.
∙ Lado exterior de la curva: 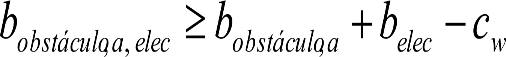
siendo belec la distancia de aislamiento eléctrico dinámica del cuadro 3.7.
La comprobación se realizará para las alturas máxima y mínima de verificación, interpolando para alturas intermedias.
3.5.2.2 Altura del gálibo eléctrico
Será la obtenida para el gálibo mecánico, incrementada en la distancia de aislamiento belec:

3.6 DISTANCIA ENTRE EJES DE VÍAS (ENTREEJE)
Se consideran dos tipos de entreeje de vías:
– Entreeje límite.
– Entreeje nominal.
Se determinan en el punto superior de la parte vertical (punto P) del contorno de referencia del gálibo cinemático de la figura 3.7.
En el caso de vías con el mismo peralte, se define el entreeje de vía Et, como la distancia ortogonal entre las normales a los planos de rodadura que pasan por los ejes de ambas. En el caso de vías con diferente peralte, será la distancia medida paralelamente a la vía de menor peralte, entre la normal al plano de rodadura por el eje de la vía de menor peralte y la paralela que pasa por el eje de la vía de mayor peralte (ver figura 3.6).
|
Figura 3.6. Entreeje de vía |
NOTA: En el caso de que las dos vías tengan el mismo peralte el entreeje teórico (Et) es la distancia ortogonal entre los ejes (normales a los planos de rodadura) de dos vías contiguas. Cada eje de vía es equidistante de los bordes activos de sus carriles.
Dada la dificultad de materializar estos ejes, lo mejor es medir mediante reglón, nivel y plomada la distancia horizontal (Em) y la diferencia de cota (z) entre los bordes activos de los hilos altos de las ambas vías y relacionar estas medidas con el entreeje teórico que está inclinado un ángulo (α) con la horizontal, siendo  el ángulo debido al peralte de la vía interior.
el ángulo debido al peralte de la vía interior.
Si los peraltes de las dos vías fueran iguales:  (z >0 si el hilo alto de la vía exterior está por encima del de la vía interior y z <0 en caso contrario). Para peraltes distintos: si son convergentes, el gálibo en las partes altas se reduce, y si son divergentes, aumenta.
(z >0 si el hilo alto de la vía exterior está por encima del de la vía interior y z <0 en caso contrario). Para peraltes distintos: si son convergentes, el gálibo en las partes altas se reduce, y si son divergentes, aumenta.
En el caso de entreeje nominal se considerará la proyección horizontal (Em).
3.6.1 PARÁMETROS QUE INTERVIENEN
a) Salientes
Definidos en el apartado 3.2.2.1.
b) Desplazamientos cuasiestáticos
Definidos en el apartado 3.2.2.2.
c) Diferencia de peralte entre ambas vías
Se considerará el acercamiento entre las partes altas de los vehículos, debido a la diferencia entre los peraltes de ambas vías, de valor:
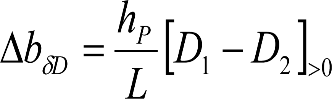
|
Figura 3.7. Distancia entre ejes de vías en el caso de peraltes diferentes |
d)Desplazamientos aleatorios laterales (MEA1+MEA2)
Definidos en el apartado 3.2.2.3.
e)Márgenes complementarios (MEA3)
Definidos en el apartado 3.2.2.4, y solo para el cálculo del entreeje nominal.
3.6.2 DETERMINACIÓN DEL ENTREEJE LÍMITE
Para determinar el entreeje límite se calculará el gálibo límite de implantación de obstáculos de cada vía, en los puntos altos del contorno de referencia, considerando que por la vía interior de la curva circula un vehículo a la velocidad máxima permitida y que en la vía exterior hay un vehículo parado con las suspensiones vencidas.
Teniendo en cuenta la escasa probabilidad de concurrencia simultánea de todos los desplazamientos aleatorios, su consideración, en ambas vías, se hará con un valor igual a K veces la media cuadrática de los mismos.
El entreeje límite se obtendrá de la expresión:

siendo:
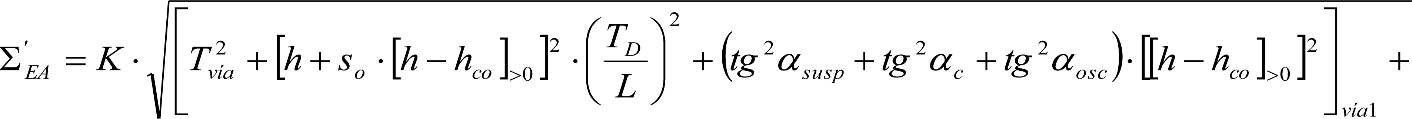
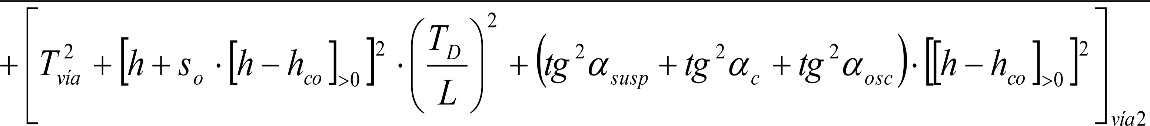
Para el cálculo del entreeje límite cuando ambas vías se encuentran en recta se calculará considerando un desplazamiento aleatorio αosc del exterior de la curva, obteniendo el entreeje de la expresión:
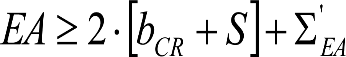

En el caso de que existan aparatos de vía será necesario verificar adicionalmente que se cumple el gálibo en aparatos de vía de acuerdo al apartado 3.7.1.2. De acuerdo a esta verificación será necesario incrementar el entreeje límite.
3.6.3 DETERMINACIÓN DEL ENTREEJE NOMINAL
El entreeje nominal se define en función del gálibo en los apartados 3.10.5.2, 3.11.5.2 y 3.12.5.2.
3.7 GÁLIBO EN ELEMENTOS ESPECÍFICOS
3.7.1 ELEMENTOS DE TRAZADO CON VARIACIÓN DE CURVATURA EN PLANTA
Los salientes y los efectos cuasiestáticos se definen, para cada alineación, en función de su radio de curvatura y su peralte. Así, en una alineación recta o curva de radio uniforme se puede establecer un gálibo único para toda ella.
Sin embargo, cuanto el primer eje de un vehículo se introduce en determinados elementos del trazado (transiciones recta-curva y aparatos de vía), los extremos de su caja ocupan un espacio que generalmente afecta a una longitud anterior a la del comienzo del elemento, y que varía progresivamente en función de las características de éste (longitud, variación del peralte y variación de la curvatura).
Análogamente, los efectos cuasiestáticos se inician con la variación del peralte, lo que a veces se produce antes del comienzo de la alineación curva.
En estos casos, puede ser necesario calcular en detalle la variación del gálibo a lo largo de la longitud afectada.
|
Figura 3.8. Efectos de la transición recta-curva |
3.7.1.1 Transiciones recta-curva
En estos casos, la variación del radio de curvatura puede ser progresiva o brusca, mientras que la variación del peralte suele ser progresiva y requiere una longitud de desarrollo mínima. En cualquier caso, los salientes y los efectos cuasiestáticos serán variables.
En el lado interior de la curva, el efecto cuasiestático es función del peralte y de la pendiente de la rampa de peralte. El punto característico del vehículo a analizar se sitúa en el centro de la caja del vehículo.
En el lado exterior de la curva, el efecto cuasiestático es función de la insuficiencia de peralte, que a su vez depende del peralte, del radio de la curva y de la velocidad. Los puntos característicos del vehículo, a analizar, se sitúan en los extremos de la caja del vehículo.
Se considerarán los casos: cambio brusco y cambio progresivo de la curvatura.
3.7.1.1.1 Cambio brusco de curvatura
a) Variación del saliente
En el lado interior de la curva, cuanto el primer bogie o eje entra en ella, las secciones internas del vehículo comienzan a desplazarse hacia el interior de la misma. Por tanto, el saliente interior se inicia a una distancia (a) antes del comienzo de la curva.
El saliente interior será máximo cuando los dos bogies o ejes del vehículo se sitúen dentro de la curva. Esto ocurre cuando la sección central del vehículo se encuentra a una distancia (a/2) dentro de la curva. Entre las secciones de inicio y de máximo desarrollo del saliente, separadas una distancia (1,5a), se tendrá una variación progresiva de éste.
En el exterior de la curva, en cuanto el primer bogie o eje entra en ella, la parte posterior del vehículo comienza a desplazarse hacia el exterior. Por tanto, el saliente exterior se inicia a una distancia (na+a) antes del comienzo de la curva.
El saliente exterior será máximo cuando los dos bogies o ejes del vehículo se sitúen dentro de la curva. Esto ocurre cuando el extremo posterior del vehículo se encuentra a una distancia (na) del inicio de la curva. Entre las secciones de inicio y de máximo desarrollo del saliente, separadas una distancia (a), se tendrá una variación progresiva de éste.
En el lado interior de la curva, la variación del saliente se produce en una distancia (1,5a). En el lado exterior, en una distancia igual al empate del vehículo (a).
Como los puntos de inicio y de máximo desarrollo del saliente son función de a y de na, será necesario determinar los valores más desfavorables para los distintos vehículos de referencia que puedan circular por la alineación que, en general, serán los de mayor longitud.
En resumen:
∙ Inicio de la transición del saliente:
‒ Interior de la curva: a una distancia a antes del comienzo de la curva.
‒ Exterior de la curva: a una distancia na+a antes del comienzo de la curva.
∙ Fin de la transición del saliente:
‒ Interior de la curva: a una distancia a/2 después del comienzo de la curva.
‒ Exterior de la curva: a una distancia na antes del comienzo de la curva.
|
Figura 3.9. Efecto de un cambio brusco de curvatura |
La definición de los valores de los parámetros a y na del vehículo de referencia se obtendrán a partir de las siguientes fórmulas:
Saliente en secciones internas 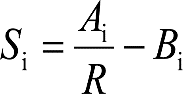
Saliente en secciones externas 

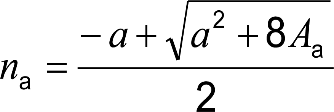
Siendo Ai y Aa coeficientes que dependen del vehículo de referencia
El semiancho del vehículo de referencia bveh será:
En el interior de la curva 
En el exterior de la curva 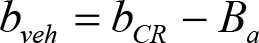
Las características de los vehículos de referencia, en función del gálibo, se definen en los apartados 3.10.8, 3.11.8 y 3.12.8.
b) Variación del efecto cuasiestático
El efecto cuasiestático se inicia y varía a lo largo de la transición del peralte.
Dicho efecto se verificará en el centro de gravedad del vehículo, que se encuentra normalmente en la sección media de la caja. La curvatura a considerar será el valor medio entre pivotes de bogies o de ejes.
c) Simplificaciones
El cálculo del espacio ocupado por los vehículos de referencia depende del radio de la curva circular. Por tanto se deberá repetir para cada radio de curva a considerar. Sin embargo, el punto de inicio y final es siempre el mismo (no depende de R). Para simplificar, puede suponerse que los salientes varían linealmente entre ambos puntos.
3.7.1.1.2 Cambio progresivo de curvatura
Las transiciones con cambio progresivo de curvatura se utilizan para velocidades elevadas(4).
(4) UNE- EN13803-1:2.011. Aplicaciones ferroviarias. Parámetros de proyecto del trazado de la vía. Ancho de vía de 1.435 mm y mayores. Parte 1. Plena vía.
UNE- EN13803-2:2.008. Aplicaciones ferroviarias. Parámetros de proyecto del trazado de la vía. Ancho de vía de 1.435 mm y mayores. Parte 2. Aparatos de vía y situaciones comparables de proyecto del trazado con variaciones bruscas de curvatura.
El caso es análogo al del apartado 3.7.1.1.1, aunque con ligeras variaciones.
∙ Inicio de la transición del saliente:
‒ Interior de la curva: a una distancia a antes del comienzo de la curva de transición.
‒ Exterior de la curva: a una distancia na+a antes del comienzo de la curva de transición.
∙ Fin de la transición del saliente:
‒ Interior de la curva: a una distancia a/2 después del comienzo de la curva circular.
‒ Exterior de la curva: na antes del comienzo de la curva circular.
En el lado interior de la curva, la variación del saliente se produce en una distancia 1,5a+long.curva transición. En el lado exterior, en una distancia a+long.curva transición.
Por tanto, las variaciones del saliente y de los efectos cuasiestáticos serán más progresivas, debido a la mayor longitud de transición de la curvatura y del peralte.
|
Figura 3.10. Efecto de un cambio progresivo de curvatura |
3.7.1.2 Aparatos de vía
El ángulo entre la vía directa y la desviada desplaza lateralmente el vehículo al atravesar su primer eje la punta matemática del aparato de vía (PMA). Este desplazamiento se produce incluso en aparatos de vía con trazado tangente. Dicho ángulo obliga al vehículo a salir, del trazado tangente teórico, hacia el exterior de la curva de la vía desviada.
El radio de curvatura puede variar mucho a lo largo del aparato de vía, con segmentos de curva inferiores a la longitud del vehículo. Estos efectos son mayores en aparatos de vía de radio pequeño.
Por tanto, un aparato de vía no puede considerarse como una curva de transición normal.
Las características de los vehículos de referencia, en función del gálibo, se definen en los apartados 3.10.8, 3.11.8 y 3.12.8. Un ejemplo de cálculo del gálibo en aparatos de vía se encuentra en el anejo E de la norma EN 15273-2:2013.
|
Figura 3.11. Efecto del ángulo de los aparatos de vía |
a) Variación del saliente
A causa del ángulo del desvío, al rebasar el primer eje del vehículo la PMA, la parte trasera del mismo se desplazará, respecto al trazado teórico, hacia el exterior de la curva de la vía desviada. Para analizar este fenómeno, los desplazamientos de los vehículos de referencia se estudiarán caso por caso mediante simulaciones, tomándose la envolvente.
Como simplificación, puede suponerse que existe una variación lineal del saliente entre el inicio del desvío y la PMA.
b) Variación de los efectos cuasiestáticos
Dado que el trazado es variable a lo largo del aparato de vía, el efecto cuasiestático teórico varía, en principio, de forma continua. Además, el ángulo de desvío a la entrada del aparato de vía crea un incremento brusco del efecto cuasiestático, como resultado de una gran insuficiencia de peralte.
|
Figura 3.12. Desplazamiento geométrico por inscripción en aparatos de vía |
c) Situación de los piquetes de vía
En la vía, el piquete es la señal que indica la posición límite donde debe detenerse la cabeza del tren delante de un desvío o semiescape por el lado del talón, para que sea compatible su posición con la circulación del tren por la otra vía.
Con carácter general la posición del piquete se situará a una distancia de cada vía, mayor o igual que la correspondiente al punto de intersección del gálibo nominal con resguardos de la vía directa con el gálibo nominal sin resguardos de la vía desviada.
En el caso de que la velocidad por vía directa sea igual o inferior a 120 km/h el piquete se podrá situar a una distancia de cada vía, mayor o igual que la correspondiente al punto de intersección del gálibo nominal sin resguardos de la vía directa con el gálibo nominal sin resguardos de la vía desviada, si bien en casos excepcionales debidamente justificados se admitirá la intersección de gálibos límites.
|
α'’: Ángulo del desvío. β’’: Angulo que define la posición del piquete respecto la vía desviada. g’: Diferencia entre el gálibo considerado en la vía directa y el semiancho de vía nominal. g’’: Diferencia entre el gálibo considerado en la vía desviada y el semiancho de vía nominal. lN: Ancho de vía nominal. d’’: Distancia entre caras internas de carril a la altura del piquete (d’’≈ g’ + g’’). PMC: Punta matemática del corazón del desvío. Figura 3.13. Posición del piquete |
A falta de cálculos específicos se podrá situar el piquete en función del gálibo de las vías directas y desviada teniendo en cuenta los siguientes valores de g’ y g’’:
∙ Gálibo GC: g’= 1,45 m y g’’ = 1,25 m
∙ Gálibo GB: g’= 1,40 m y g’’ = 1,20 m
∙ Gálibos GHE16, GEB16 y GEC16: g’= 1,35 m y g’’ = 1,15 m
∙ Gálibos GED10 y GEE10: g’= 1,50 m y g’’ = 1,30 m
En el caso de los escapes:
∙ Para entreejes menores a 4,0 m el piquete se situará en la junta de contraagua.
∙ Para entreejes superiores a 4,0 m el piquete se situará a una distancia de cada vía, mayor o igual que la correspondiente al punto de intersección del gálibo nominal con resguardos de la vía directa con el gálibo nominal sin resguardos de la vía desviada. A falta de cálculos específicos podrá situarse el piquete conforme lo indicado anteriormente.
3.7.2 ANDENES
En este apartado se definen los gálibos que deben respetar los andenes, con el fin de permitir: el paso de los vehículos, el funcionamiento adecuado de sus estribos, peldaños abatibles, rampas escamoteables y la apertura de sus puertas (en caso de andenes altos).
Se situarán fuera del gálibo límite de implantación obstáculos.
Se deberá asegurar que los escalones de seguridad que permiten al personal salir de la vía, respeten siempre el gálibo de partes bajas.
Los andenes se dispondrán a una distancia horizontal mínima respecto a la vertical por el eje de la vía igual a:
∙ Lado interior de la curva:

∙ Lado exterior de la curva:
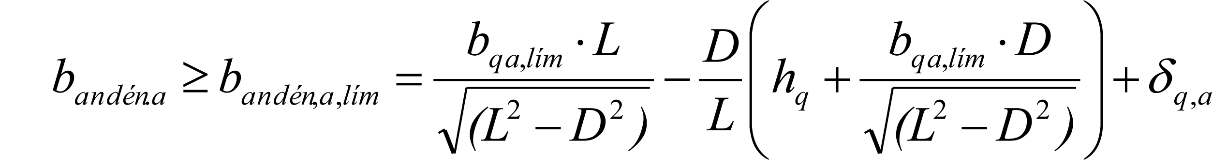
siendo:
hq: Altura del borde de andén, medida sobre el plano de rodadura y perpendicularmente a éste.
L: Distancia entre círculos de rodadura.
D: Peralte.
δq,a: Separación horizontal del andén en el lado exterior de la curva respecto el gálibo límite de implantación de obstáculos inclinado un ángulo δ.
a) En el caso de presencia de bordillo retranqueado:
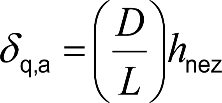
Siendo hnezla altura del bordillo del borde de andén.
|
(1) Andén (2) Gálibo límite de implantación de obstáculos (3) Escalón de seguridad para el personal Figura 3.14. δq,a en el caso de andén con bordillo retranqueado |
b) En el caso de andén vertical recto:
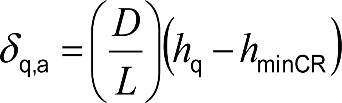
Siendo hminCRla altura de la esquina inferior del contorno de referencia.
|
(1) Andén (2) Gálibo límite de implantación de obstáculos (3) Escalón de seguridad para el personal Figura 3.15. δq,a en el caso de andén sin bordillo retranqueado |
bqi, bqa: Distancia entre la perpendicular al plano de rodadura en el eje de la vía y el borde del andén, medida en una sección transversal, paralelamente al plano de rodadura y hacia el interior y exterior de la curva, respectivamente (figs. 3.16 y 3.17). Sus valores serán:

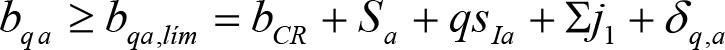
siendo:
bCR: Semiancho del contorno de referencia

|
Figura 3.16: Determinación de b andén en andén de paramento vertical recto. |
|
|
Figura 3.17: Determinación de b andén en andén de paramento vertical retranqueado. |
|
|
Figura 3.18: Parámetros bandén i/a y hq. |
|
La separación del andén respecto el eje de la vía deberá estar comprendida entre los siguientes límites:
a) Considerando la separación respecto un plano horizontal:

Siendo Tq las tolerancias para la construcción y mantenimiento definidas en los apartados 3.10.6 y 3.11.6.
b) Considerando la separación respecto un plano paralelo al plano de rodadura:
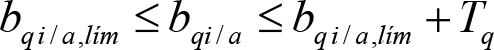
La separación del andén se determinará comprobando todos los puntos del contorno de referencia que queden por debajo de la altura de dicho andén, teniendo en cuenta su tipología y forma.
Por encima del andén se dejará libre de obstáculos una banda de al menos 20 cm a fin de permitir la apertura de espejos retrovisores, puertas de acceso, etc.
No se colocarán andenes a los lados de las vías en las que esté prevista la circulación de transportes excepcionales.
En el caso de que existan aparatos de vía en los andenes será necesario verificar adicionalmente que se cumple el gálibo en aparatos de vía de acuerdo al apartado 3.7.1.2. De acuerdo a esta verificación será necesario incrementar la separación de los andenes.
En líneas de ancho ibérico o estándar europeo, la altura de los andenes (hq) será de 55, 68 ó 76 cm sobre el plano de rodadura. En las de ancho métrico será de 105 cm.
Las distancias del borde del andén al eje de la vía, para distintos anchos de vía, se definen en los apartados 3.10.6, 3.11.6 y 3.12.6.
Como la medida de hq es complicada, al estar referida al plano de rodadura, se medirán con regla, plomada y nivel las magnitudes hi, Li, he y Le (fig. 3.19). A partir de ellas, se obtendrán hq y banden,i/a, mediante las fórmulas siguientes:
|
Figura 3.19. Andenes |
∙ Lado interior de la curva: 
∙ Lado exterior de la curva: 
siendo δ el ángulo del peralte:
3.7.3 PASILLOS DE EVACUACIÓN EN TÚNELES
Estos pasillos son exigidos por la Especificación Técnica de Interoperabilidad de seguridad en túneles ferroviarios para túneles nuevos.
El borde de la acera estará situado en el límite del gálibo nominal de implantación de obstáculos, para la posición más desfavorable del peralte. En casos excepcionales debidamente justificados, la Autoridad Ferroviaria podrá autorizar que la acera se sitúe respetando únicamente el gálibo límite de implantación de obstáculos.
En túneles de vía única, en los que no exista un itinerario alternativo para el paso de transportes excepcionales, solo se colocarán aceras por encima de la cota de carril, a un lado del túnel, salvo autorización en contrario de la Autoridad Ferroviaria. El borde de la acera se situará conforme lo indicado en el párrafo anterior.
3.7.4 PASEOS DE SERVICIO PARA MANTENIMIENTO
Los paseos de servicio para mantenimiento se definirán de acuerdo a otras Instrucciones Ferroviarias. En todo caso, en los paseos se evitará la implantación de instalaciones, fijas o provisionales, u otros elementos que dificulten o impidan el paso de personas, observando las medidas de protección necesarias y garantizando la seguridad de las circulaciones.
3.7.5 MUELLES
No se colocarán muelles junto a:
▪ Vías generales o de circulación.
▪ Vías con peralte.
El borde del muelle, estará situado fuera del gálibo límite de implantación de obstáculos.
3.7.6 APEOS DE VÍA
En el caso de que sea necesario apear la vía para llevar a cabo obras como la ejecución de cajones empujados y cruces de tubos deberá verificarse el gálibo de implantación de obstáculos de partes bajas correspondiente y tener en cuenta las condiciones particulares de explotación.
3.7.7 GÁLIBO EN ZONA DE OBRAS AUTORIZADAS POR EL ADMINISTRADOR DE INFRAESTRUCTURA
La situación de los elementos móviles, las personas y la maquinaria no es objeto de la presente Instrucción.
En el caso de los elementos fijos se distinguirán dos casos:
∙ Elementos permanentes:
Se demostrará que cumplen con carácter general, el gálibo uniforme de implantación de obstáculos definido para línea de acuerdo al apartado 1.3.2.
∙ Elementos provisionales:
Se demostrará que cumplen el gálibo nominal, si bien en el caso de que la velocidad sea igual o inferior a 120 km/h se podrán situar verificando el gálibo nominal sin resguardos. En casos excepcionales debidamente justificados se podrá utilizar el gálibo límite.
Los transportes excepcionales con rebase de gálibo, pueden llegar a utilizar al máximo el hueco disponible en zonas como túneles, pasos superiores, andenes, etc., por lo que cuando sea necesaria la colocación de elementos, tanto permanentes como provisionales, que supongan una restricción a la circulación de esos transportes, se deberá comunicar al organismo encargado de autorizarlos la afectación que estas actuaciones puedan tener en su realización.
3.8 TRANSICIONES DE LOS FRENOS DE VÍA EN POSICIÓN ACTIVA
Los frenos de vía en posición activa pueden elevarse hasta una altura máxima de 0,115/0,125 m sobre el plano de rodadura en las secciones siguientes:
∙ A una distancia como mínimo de x = 3m, del final de un acuerdo convexo de radio Rv ≥ 250m. Esta distancia se amplía a x = 5m en el caso de lomos de asno por los que vayan a circular ciertos tipos de vagones, como los utilizados en transporte combinado.
∙ En acuerdos cóncavos de Rv ≥ 300m o en sus proximidades.
|
Figura 3.20. Transiciones de los frenos de vía en posición activa |
|||||||||||||||||||||
Sea x la distancia desde el final del acuerdo vertical a la sección considerada.
En el tramo entre el final del acuerdo convexo (x = 0) y x = 3m o x = 5m, las alturas de 0,115/0,125 m, a las que pueden elevarse los frenos de vía, se reducirán los valores siguientes:
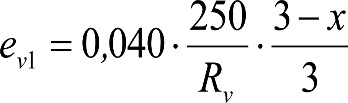 (lomos de asno clásicos con x=3m)
(lomos de asno clásicos con x=3m)
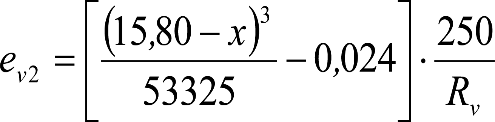 (lomos de asno donde operen ciertos vagones, como los de transporte combinado, con x=5m)
(lomos de asno donde operen ciertos vagones, como los de transporte combinado, con x=5m)
La reducción máxima se da en la sección final del acuerdo convexo (x = 0), con un valor de:
 (lomos de asno clásicos con x=3m)
(lomos de asno clásicos con x=3m)
 (lomos de asno donde operen ciertos vagones, como los de transporte combinado, con x=5m)
(lomos de asno donde operen ciertos vagones, como los de transporte combinado, con x=5m)
|
Figura 3.21. Reducciones en altura de los frenos de vía en posición activa |
3.9 VEHÍCULOS DE CAJA INCLINABLE
El gálibo de implantación de obstáculos se define para la velocidad máxima de la línea establecida para los trenes convencionales. Los vehículos de caja inclinable que circulen a velocidades superiores a la de la línea deberán respetar el gálibo de implantación de obstáculos.
El vehículo de caja inclinable dispondrá de los mecanismos necesarios para asegurar que respeta el gálibo de implantación de obstáculos en: línea recta, alineaciones circulares, curvas de transición, e incluso en el caso de fallo del sistema de inclinación de la caja.
Por tanto, en cualquier situación, los valores de I’c e I’p serán tales que:

Si el valor de la relación ![]() fuera inferior, el Administrador de la Infraestructura tomará las medidas necesarias para cumplir con dicho límite.
fuera inferior, el Administrador de la Infraestructura tomará las medidas necesarias para cumplir con dicho límite.
El Administrador de la Infraestructura debe comprobar la máxima velocidad local de la línea en base a la fórmula:
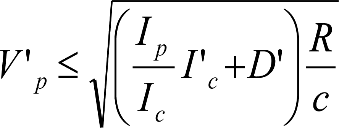
donde: 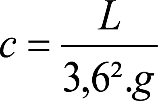 y g = 9,81 m/s².
y g = 9,81 m/s².
Si la siguiente condición se cumple:
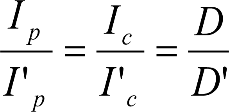
Entonces: 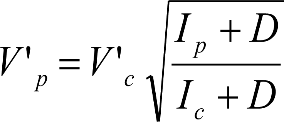
Esta fórmula establece una relación constante entre la velocidad de los trenes clásicos y de los pendulares.
Estas verificaciones forman la base de un acuerdo entre la infraestructura y el vehículo.
3.10 APLICACIÓN A LÍNEAS CON ANCHO IBÉRICO
3.10.1 REGLAS ASOCIADAS
3.10.1.1 Salientes
Se considerarán los salientes Si y Sa recogidos en el apartado 2.7.2.4.
Como ancho de vía, se tomará el valor:
∙ l = lmáx = lN + sobre ancho máximo = lN +0,03 = 1,698m (para cálculo de los gálibos límite, nominal y uniforme de implantación de obstáculos así como para el entreeje límite y nominal).
siendo: lN=1,668m.
3.10.1.2. Desplazamientos cuasiestáticos laterales (solo para h>hco)
Se obtendrán particularizando las fórmulas del apartado 3.2.2.2, para los siguientes valores:
∙ L = 1,733m
∙ D0 = I0 = 0,05m
∙ hco = 0,5m
∙ so: definido en el cuadro 2.9 del apartado 2.7.2.4 para distintos gálibos y alturas.
Los desplazamientos cuasiestáticos de cualquier punto del vehículo situado a una altura h respecto al plano de rodadura, serán:
∙ Hacia el interior de la curva (puntos del contorno interior y exterior del vehículo):

∙ Hacia el exterior de la curva (puntos del contorno interior y exterior del vehículo):

3.10.1.3 Desplazamientos aleatorios laterales y perpendiculares al plano de rodadura
Se obtendrán particularizando las fórmulas de los apartados 3.2.2.3 y 3.2.3.3, con los valores de los parámetros indicados en el cuadro 3.8.
| Parámetros |
Símbolo |
Vía en balasto | Vía en placa | |||
|---|---|---|---|---|---|---|
| Interior de la curva | Exterior de la curva | Interior de la curva | Exterior de la curva | |||
| Desplazamiento de vía | Tvía | 0,025 m | 0,025 m | 0,005 m | 0,005 m | |
|
Desviac. del peralte |
Vmáx 80 km/h | TD | 0,020 m | 0,020 m | 0,005 m | 0,005 m |
| Vmáx>80 km/h | 0,015 m | 0,015 m | 0,005 m | 0,005 m | ||
| Disimetría debida al reparto de cargas | α c | 0,77.º | 0,77.º | 0,77.º | 0,77.º | |
| Disimetría debida al reglaje de las suspensiones | α susp | 0,23.º | 0,23.º | 0,23.º | 0,23.º | |
3.10.1.4 Márgenes complementarios laterales (M3b) y verticales (M3h)
|
Oscilaciones por irregularidades |
Vías en buen estado | α osc (1) | 0,1.º(para s o 0,4) | 0,6.º(para s o 0,4) |
0,1.º(para so 0,4) 0,08.º(para so 0,3) |
0,6.º(para so 0,4) 0,45.º(para so 0,3) |
| 0,08.º(para s o 0,3) | 0,45.º(para s o 0,3) | |||||
| Vías en mal estado | 0,2.º(para s o 0,4) | 1.º(para s o 0,4) | ||||
| 0,15.º(para s o 0,3) | 0,75.º(para s o 0,3) | |||||
| Desplazamiento vertical de la vía | T N |
Para las partes bajas entre carriles y para aquellos obstáculos que se muevan solidariamente con la vía: 5mm. En el caso de obstáculos que no se muevan solidariamente con la vía: 20mm
|
||||
| Factor de seguridad para la determinación del gálibo límite de implantación de obstáculos | K |
1,2 en general 1 (en el caso de los desplazamientos aleatorios laterales para h<0,5m) |
||||
| Factor de seguridad para la determinación del gálibo mecánico del pantógrafo | K’ | 1 | ||||
|
(1)Nota: Los valores de αosc indicados se utilizarán para el cálculo de los desplazamientos laterales. En el caso de los desplazamientos verticales se tomarán del lado interior de la curva los valores del lado exterior de la curva y del lado exterior de la curva los valores del lado interior de la curva. |
||||||
|
Cuadro 3.8. Parámetros para el cálculo de los desplazamientos aleatorios en los gálibos GHE16, GEA16, GEB16 y GEC16 |
||||||
Se consideran los siguientes valores:
∙ Márgenes horizontales (M3b):
– 0,200 m para los puntos con h>0,4m.
– 0,200 m y 0 para h=0,4 m. En este punto se produce una discontinuidad en el gálibo nominal
– 0 para puntos con h<0,4 m.
∙ Márgenes verticales (M3h):
– 0,150 m para los puntos con h>0,4m.
– 0,150 m y 0 para h=0,4 m. En este punto se produce una discontinuidad en el gálibo nominal
– 0 para puntos con h<0,4 m.
3.10.1.5 Inscripción en acuerdos verticales
El radio del acuerdo vertical Rv ≥ 500m.
– Las cotas verticales de los puntos del contorno de referencia por encima de la anchura máxima se aumentarán en 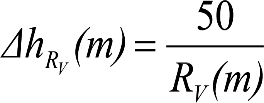 y los puntos del contorno de referencia por debajo de la anchura máxima se reducirán en
y los puntos del contorno de referencia por debajo de la anchura máxima se reducirán en 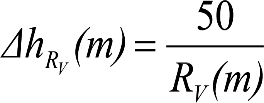
– Las cotas verticales de las partes bajas, fuera de la zona de ruedas, del contorno de referencia se reducirán en el mismo valor. En el caso de 500 m ≤ Rv ≤ 625 m y para cotas iguales o inferiores a 80 mm, como las reducciones serían mayores que la altura del contorno de referencia, solo se considerará una reducción igual a la distancia entre el contorno de referencia y el plano de rodadura.
3.10.1.6 Desplazamientos cuasiestáticos perpendiculares al plano de rodadura
Se obtendrán particularizando las fórmulas del apartado 3.2.3.2, para los siguientes valores:
∙ L=1,733m
∙ D0 = I0 = 0,05m
∙ hco=0,5m
∙ so: definido en el cuadro 2.9 del apartado 2.7.2.4 para distintos gálibos y alturas.
Los desplazamientos cuasiestáticos verticales causados por D e I, para los puntos PT, situados a una altura hPT respecto al plano de rodadura y a una distancia horizontal bPT respecto al eje de la vía, serán:
∙ Vehículo parado con peralte D:

(descenso en el lado interior de la curva y elevación en el exterior)
∙ Vehículo circulando con insuficiencia de peralte I:

(elevación en el lado interior de la curva y descenso en el exterior)
3.10.1.7 Margen perpendicular al plano de rodadura en la zona de ruedas
En la zona de ruedas con el fin de no dificultar el paso de la pestaña (por ejemplo entarimados de pasos a nivel, pasos entre vías, etc), deberá tenerse en cuenta un margen a fin de considerar el desgaste de los carriles.
La zona de ruedas queda delimitada por los puntos del contorno de referencia situados en el intervalo 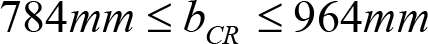
La zona de ruedas para los gálibos GEI1, GEI2 y GEI3 se define en las figuras 3.22 y 3.23.
|
l : Ancho de vía Figura 3.22. Zona de ruedas del gálibo GEI1 |
|
l : Ancho de vía Figura 3.23. Zona de ruedas de los gálibos GEI2 y GEI3 |
3.10.2 GÁLIBO LÍMITE DE IMPLANTACIÓN DE OBSTÁCULOS
En los cuadros 3.9 y 3.10 se indican las fórmulas a emplear en cada caso y situación, tomadas de las situaciones generalmente más desfavorables del cuadro 3.1, siendo:



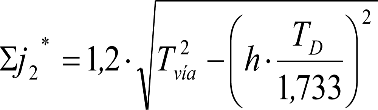

El signo [ ]>0 significa que cuando la expresión entre paréntesis es positiva, mantiene su valor, y cuando es negativa o nula, se toma cero.
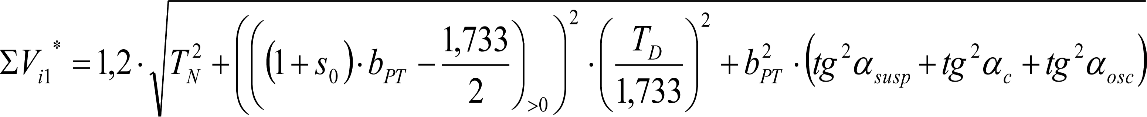
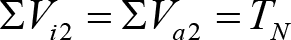
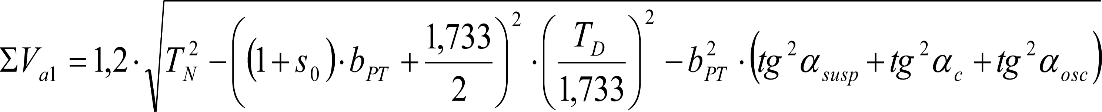
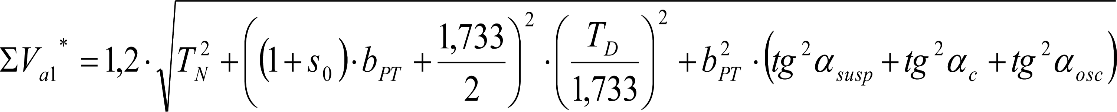
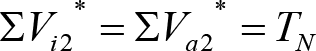
| V máx (I) | Punto PT | Lado exterior de la curva | bobstáculo máximo con h obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes bajas (h≤0,4m) | hobstáculo máximo con b obstáculo compatible |
|
||
| Punto PT | Lado interior de la curva | hobstáculo máximo con b obstáculo compatible |
|
|
| Partes altas:puntos por encima de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes bajas (h≤0,4m) | bobstáculo máximo con h obstáculo compatible |
|
||
|
Cuadro 3.9 Fórmulas consideradas con vehículo circulando a Vmáx (I), correspondientes a las situaciones generalmente más desfavorables |
||||
|
V=0 (D) |
Punto PT | Lado exterior de la curva | hobstáculo máximo con b obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes bajas (h≤0,4m) | bobstáculo máximo con h obstáculo compatible |
|
||
| Punto PT | Lado interior de la curva | bobstáculo máximo con h obstáculo compatible |
|
|
| Partes altas:puntos por encima de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes bajas (h≤0,4m) | hobstáculo máximo con b obstáculo compatible |
|
||
|
Cuadro 3.10. Fórmulas consideradas con vehículo parado (D) ), correspondientes a las situaciones generalmente más desfavorables |
||||
3.10.3 GÁLIBO NOMINAL DE IMPLANTACIÓN DE OBSTÁCULOS
Los márgenes considerados son los siguientes:
a) Márgenes horizontales
M3b = 0,200 m en los puntos del contorno de referencia con h>0,4m.
M3b = 0,200 m y 0 en h=0,4m. Se produce una discontinuidad en el gálibo nominal.
M3b = 0 en los puntos bajos del contorno de referencia (h<0,4m).
b) Márgenes verticales
M3h = 0,150 m en los puntos del contorno de referencia con h>0,4m.
M3h = 0,150 m y 0 en h=0,4m. Se produce una discontinuidad en el gálibo nominal.
M3h = 0 en los puntos bajos del contorno de referencia (h<0,4m).
En los cuadros 3.11 y 3.12 se indican las fórmulas a emplear en cada caso y situación, tomadas de las situaciones generalmente más desfavorables del cuadro 3.3, siendo:


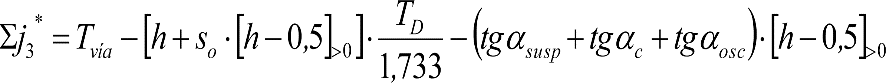


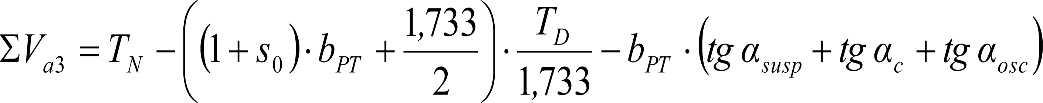
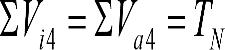
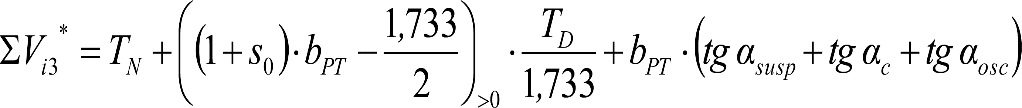

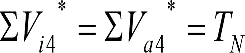
|
V máx (I) |
Punto PT | Lado exterior de la curva | bobstáculo máximo con h obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| h=0,4m | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes bajas (h<0,4m) | hobstáculo máximo con b obstáculo compatible |
|
||
|
V máx (I) |
Punto PT | Lado interior de la curva | hobstáculo máximo con b obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| h=0,4m | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes bajas (h<0,4m) | bobstáculo máximo con h obstáculo compatible |
|
||
|
Cuadro 3.11. Fórmulas consideradas con vehículo circulando a Vmáx (I) ), correspondientes a las situaciones generalmente más desfavorables |
||||
|
V=0 (D) |
Punto PT | Lado exterior de la curva | hobstáculo máximo con b obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| h=0,4m | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes bajas (h<0,4m) | bobstáculo máximo con h obstáculo compatible |
|
||
| Punto PT | Lado interior de la curva | bobstáculo máximo con h obstáculo compatible |
|
|
| Partes altas:puntos por encima de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| h=0,4m | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes bajas (h<0,4m) | hobstáculo máximo con b obstáculo compatible |
|
||
|
Cuadro 3.12. Fórmulas consideradas con vehículo parado (D) ), correspondientes a las situaciones generalmente más desfavorables |
||||
3.10.4 GÁLIBO DEL PANTÓGRAFO
3.10.4.1 Contorno de referencia del pantógrafo
Como contornos de referencia para pantógrafos de 1.950 mm o 1.600 mm de ancho se tomarán los representados en las figuras 3.24 y 3.25, respectivamente.
|
Figura 3.24. Contorno de referencia para pantógrafos de 1.950 mm de ancho en posición de captación. |
|
Figura 3.25. Contorno de referencia para pantógrafos de 1.600 mm de ancho en posición de captación. |
3.10.4.2 Valor de los parámetros
∙ Semiancho de la mesilla del pantógrafo (bw): definido en el cuadro 3.5 del apartado 3.5.1.1.
∙ Desplazamientos laterales máximos del pantógrafo:
∙ epo = 0,170 m, a la máxima altura de verificación h’0 = 6,5 m
∙ epu = 0,110 m, a la mínima altura de verificación h’u = 5 m
∙ Salientes: 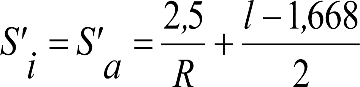
∙ L = 1,733 m
∙ s’0 = 0,225
∙ h’c0 = 0,5 m
∙ D’o = I’o = 1/15 ≈ 0,066 m
∙ Desplazamientos cuasiestáticos horizontales:
∙ Lado interior curva:
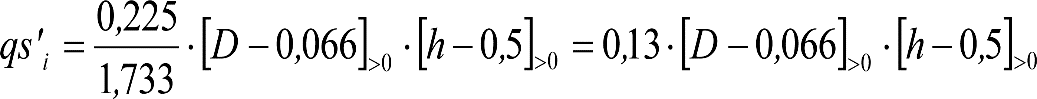
∙ Lado exterior curva:

∙ Desplazamientos aleatorios: definidos en el cuadro 3.8 del apartado 3.10.1.3.
Se tomarán los siguientes valores deαosc:
– Para vía en balasto en buen estado: 0,06.º del lado interior de la curva y 0,34.º del lado exterior de la curva.
– Para vía en balasto en mal estado: 0,11.º del lado interior de la curva y 0,6.º del lado exterior de la curva.
– Para vía en placa: 0,06.º del lado interior de la curva y 0,34.º del lado exterior de la curva.
∙ cw = 0,2 (en líneas existentes, para pantógrafos con trocadores aislados).
∙ cw = 0 (en líneas nuevas o acondicionadas, para permitir pantógrafos con trocadores no aislados).
3.10.4.3 Anchura del gálibo mecánico
Se considerarán las siguientes expresiones:
∙ Lado interior de la curva:
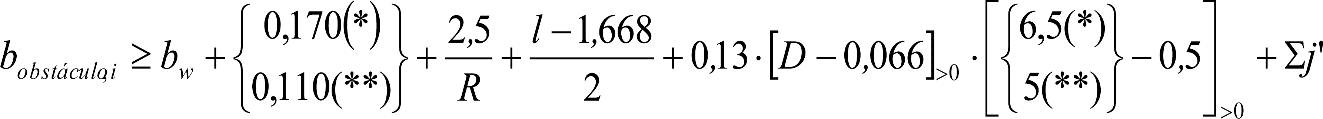
∙ Lado exterior de la curva:
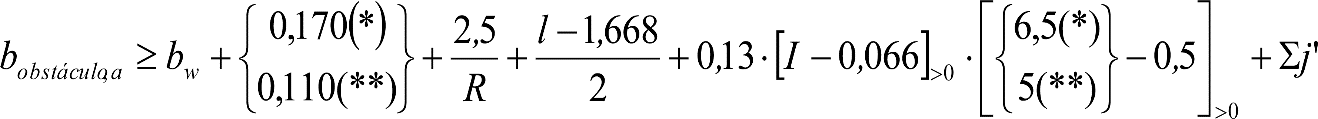
siendo:
bw: semiancho de la mesilla del pantógrafo, definido en el cuadro 3.5 del apartado 3.5.1.1.

(*) Valor a aplicar para la altura máxima de verificación; (**) Valor a aplicar para la altura mínima de verificación. Se interpolará para alturas intermedias.
3.10.4.4 Anchura del gálibo eléctrico
Se obtendrá a partir de las expresiones del apartado 3.5.2.1, particularizando para los valores de bobstáculo obtenidos en el apartado anterior, de belec definida en el cuadro 3.7 del apartado 3.5.2, y de cw = 0,2 (en líneas existentes, para pantógrafos con trocadores aislados) o cw = 0 (en líneas nuevas o acondicionadas, para permitir pantógrafos con trocadores no aislados).
3.10.4.5 Alturas de los gálibos mecánico y eléctrico
Se determinarán según lo indicado en los apartados 3.5.1.3 y 3.5.2.2
3.10.5 DISTANCIA ENTRE EJES DE VÍAS
3.10.5.1 Determinación del entreeje límite
Se obtendrá de la expresión

siendo:
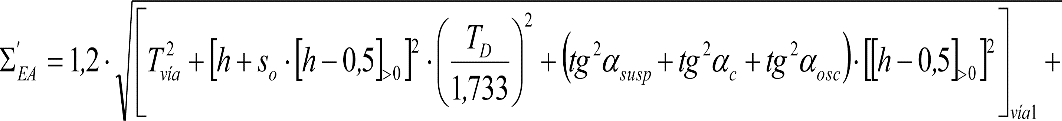

3.10.5.2 Determinación del entreeje nominal
Se define en el cuadro 3.13, en función de la velocidad máxima del tramo de la línea:
| Velocidad (km/h) | Entreeje nominal (mm) |
|---|---|
| Vmax ≤ 140 | 3.808 |
| 140 < V max ≤ 200 | 4.000 |
| 200 < V max < 250 | 4.300 |
| 250 ≤ V max ≤ 350 | 4.700 |
|
Cuadro 3.13. Distancia nominal entre ejes de vías (valores normales) |
|
Los valores dados en el cuadro anterior son mínimos y se medirán en la proyección horizontal. En líneas de altas prestaciones con tráfico mixto se adoptarán las medidas operacionales que sean necesarias para garantizar la seguridad de la circulación, tales como las definidas en la ETI de infraestructura de alta velocidad en el caso de vientos laterales así como las debidas condiciones de estibaje para evitar desplazamientos de la carga.
En casos excepcionales debidamente justificados, la distancia entre ejes de vías podrá definirse de acuerdo al cuadro 3.14, siendo necesario para este caso realizar un estudio específico que determine el valor mínimo necesario del entreeje en función de las condiciones de explotación.
| Velocidad (km/h) | Entreeje nominal (mm) |
|---|---|
| Vmax ≤ 160 | 3808 |
| 160 < V max ≤ 200 |
3808 (ancho de vía 1435 mm) 3920 (ancho de vía 1668 mm, o una vía en ancho 1435 mm y la otra en ancho 1668 mm) |
| 200 < V max < 250 | 4000 |
| 250 ≤ V max ≤ 300 | 4300 |
| 300 < V max ≤ 350 | 4500 |
|
Cuadro 3.14. Distancia nominal entre ejes de vías (valores excepcionales) |
|
En el caso de que la velocidad del tramo de la línea sea igual o inferior a 120 km/h se admitirá una distancia entre ejes de vías inferior a 3808 mm, siempre y cuando se demuestre la seguridad de la circulación de los trenes, comprobando que se cumple al menos el entreeje límite definido en el apartado 3.10.5.1.
3.10.6 DISTANCIA ENTRE EJE DE VÍA Y BORDE DE ANDÉN
Bajo las siguientes hipótesis:
∙ Sobreancho máximo: 30 mm
∙ Peralte máximo: D = 0,115 m
∙ Insuficiencia de peralte: Imax = 0,115 m
∙ Vía en balasto, en mal estado.
∙ Cálculos realizados para andén vertical recto, sin bordillo retranqueado.
En los andenes donde no se cumplan las hipótesis anteriores, la determinación de la distancia entre eje de vía y borde de andén requerirá un estudio específico.
| Altura del andén (h q), en mm. | Borde de andén | Radio de la curva (R), en m | |||||
|---|---|---|---|---|---|---|---|
| R ≥ 5000 m | 5000 > R ≥ 1000 m | 1000 > R ≥ 250 m | |||||
| Peralte (D ), en mm | |||||||
| D=0 | D=115 mm | D=0 | D=115 mm | D=0 | D=115 mm | ||
| 760 | Exterior | 1750 | 1750(*) | 1755 | 1755(*) | 1765 | 1765(*) |
| Interior | 1750 | 1795 | 1755 | 1800 | 1765 | 1810 | |
| 680 | Exterior | 1745 | 1745(*) | 1750 | 1750(*) | 1760 | 1760(*) |
| Interior | 1745 | 1790 | 1750 | 1790 | 1760 | 1805 | |
| (*) Para el caso de andén exterior y vía con peralte conviene utilizar el valor correspondiente a vía sin peralte, en previsión de un posible cambio durante la vida de la vía a peralte cero. | |||||||
|
Cuadro 3.15. Distancia de borde de andén a eje de vía (bandén,i/a,lím) |
|||||||
con las tolerancias indicadas en el cuadro 3.16.
| Actuación en vía | Tolerancias (mm) | |
|---|---|---|
| h q | T q | |
| Construcción, acondicionamiento o renovación de vía | (0;-10) | 10 |
| Mantenimiento de vía | (0;-30) | 30 |
|
Cuadro 3.16. Tolerancias en andenes |
||
3.10.7 GÁLIBO UNIFORME DE IMPLANTACIÓN DE OBSTÁCULOS
Si se cumplen las siguientes hipótesis:
∙ Radio mínimo en planta: R = 250 m
∙ Radio mínimo de acuerdo vertical: Rv = 2.000 m
∙ Sobreancho máximo: 30 mm
∙ Peralte máximo: D = 0,160 m
∙ Insuficiencia de peralte máxima: Imax= 0,175 m
∙ TN en partes bajas: 5 mm.
∙ Vía en balasto, en mal estado.
∙ Catenaria CA-160.
∙ Pantógrafo con ancho de la mesilla 2xbw= 1.950 mm y trocadores no aislados cw=0.
∙ Balizas ASFA situadas en acuerdos verticales de radio superior a 4.000 m y sistemas de señalización mediante ERTMS y LZB con independencia del radio de acuerdos verticales.
los gálibos uniformes GEB16 y GEC16, serán los definidos en las figuras 3.26 y 3.27. En aquellos puntos donde no se cumplan las hipótesis anteriores, la determinación del gálibo nominal de implantación de obstáculos requerirá un estudio específico.
Los ejes X y Y, son respectivamente, paralelo y perpendicular al plano de rodadura.
|
Figura 3.26. Gálibo uniforme GEB16 |
|
Figura 3.27. Gálibo uniforme GEC16 |
3.10.8 CARACTERÍSTICAS DE LOS VEHÍCULOS DE REFERENCIA
Para el cálculo del gálibo de implantación de obstáculos en las zonas de aparatos de vía o curvas de transición se considerarán los vehículos de referencia definidos en el cuadro 3.17.
| Gálibo |
hmin [mm] |
hmax [mm] |
bCR [mm] |
Ai [m] |
Aa [m] |
B i,a [mm] |
bveh [mm] |
a [m] |
na [m](5 m) | na [m](20 m) |
|---|---|---|---|---|---|---|---|---|---|---|
| GHE16/GEC16 | 400 | max. | 1 720 | 3,75 | 1 720 | 5,477 | ||||
| GHE16/GEC16 | 400 | max. | 1 720 | 3,75 | 1 720 | 1,208 | 0,368 | |||
| GHE16/GEC16 | 400 | max. | 1 720 | 50 | 185 | 1 535 | 20,000 | |||
| GHE16/GEC16 | 400 | max. | 1 720 | 60 | 225 | 1 495 | 8,736 | 4,832 | ||
| GEB16 | 400 | 3 320 | 1 720 | 3,75 | 1 720 | 5,477 | ||||
| GEB16 | 400 | 3 320 | 1 720 | 3,75 | 1 720 | 1,208 | 0,368 | |||
| GEB16 | 400 | 3 320 | 1 720 | 50 | 185 | 1 535 | 20,000 | |||
| GEB16 | 400 | 3 320 | 1 720 | 60 | 225 | 1 495 | 8,736 | 4,832 | ||
| GEB16 | 4 110 | max. | 1 720 | 20 | 1 720 | 12,649 | ||||
| GEB16 | 4 110 | max. | 1 720 | 20 | 1 720 | 4,301 | 1,832 | |||
| GEB16 | 4 110 | max. | 1 720 | 50 | 120 | 1 600 | 20,000 | |||
| GEB16 | 4 110 | max. | 1 720 | 50 | 120 | 1 600 | 7,808 | 4,142 | ||
|
Cuadro 3.17. Características de los vehículos de referencia en los gálibos GHE16, GEB16 y GEC16 |
||||||||||
3.11 APLICACIÓN A LÍNEAS CON ANCHO ESTÁNDAR EUROPEO
3.11.1 REGLAS ASOCIADAS
3.11.1.1 Salientes
Se considerarán los salientes Si y Sa recogidos en el apartado 2.8.2.4.
Como ancho de vía, se tomará el valor:
∙ l = lmáx = lN + sobre ancho máximo = lN +0,03 = 1,465m (para cálculo de los gálibos límite, nominal y uniforme de implantación de obstáculos así como para el entreeje límite y nominal).
siendo: lN=1,435m.
3.11.1.2 Desplazamientos cuasiestáticos laterales (solo para h>hco)
Se obtendrán particularizando las fórmulas del apartado 3.2.2.2, para los siguientes valores:
∙ L = 1,500m
∙ D0 = I0 = 0,050m
∙ hco = 0,500m
∙ so: definido en el cuadro 2.16 del apartado 2.8.2.4 para distintos gálibos y alturas.
Los desplazamientos cuasiestáticos de cualquier punto del vehículo situado a una altura h respecto al plano de rodadura, serán:
∙ Hacia el interior de la curva (puntos del contorno interior y exterior del vehículo):

∙ Hacia el exterior de la curva (puntos del contorno interior y exterior del vehículo):

3.11.1.3 Desplazamientos aleatorios laterales y perpendiculares al plano de rodadura
Se obtendrán particularizando las fórmulas de los apartados 3.2.2.3 y 3.2.3.3, con los valores de los parámetros indicados en el cuadro 3.8.
3.11.1.4 Márgenes complementarios laterales (M3b) y verticales (M3h)
Se consideran los siguientes valores:
∙ Márgenes horizontales (M3b):
– 0,200 m para los puntos con h>0,4m.
– 0,200 m y 0 para h=0,4 m. En este punto se produce una discontinuidad en el gálibo nominal
– 0 para puntos con h<0,4 m.
∙ Márgenes verticales (M3h):
– 0,150 m para los puntos con h>0,4m.
– 0,150 m y 0 para h=0,4 m. En este punto se produce una discontinuidad en el gálibo nominal
– 0 para puntos con h<0,4 m.
3.11.1.5 Inscripción en acuerdos verticales
El radio del acuerdo vertical Rv ≥ 500m.
– Las cotas verticales de los puntos PT del contorno de referencia por encima de la anchura máxima se aumentarán en 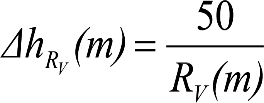 y los puntos del contorno de referencia por debajo de la anchura máxima se reducirán en
y los puntos del contorno de referencia por debajo de la anchura máxima se reducirán en 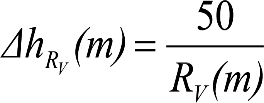
– Las cotas verticales de las partes bajas, fuera de la zona de ruedas, del contorno de referencia se reducirán en el mismo valor. En el caso de 500 m ≤ Rv ≤ 625 m y para cotas iguales o inferiores a 80 mm, como las reducciones serían mayores que la altura del contorno de referencia, solo se considerará una reducción igual a la distancia entre el contorno de referencia y el plano de rodadura.
3.11.1.6 Desplazamientos cuasiestáticos perpendiculares al plano de rodadura
Se obtendrán particularizando las fórmulas del apartado 3.2.3.2, para los siguientes valores:
∙ L=1,500m
∙ D0 = I0 = 0,050m
∙ hco=0,5m
∙ so: definido en el cuadro 2.16 del apartado 2.8.2.4 para distintos gálibos y alturas.
Los desplazamientos cuasiestáticos verticales causados por D e I, para los puntos PT PT, situados a una altura hPT respecto al plano de rodadura y a una distancia horizontal bPT respecto al eje de la vía, serán:
∙ Vehículo parado con peralte D:

(descenso en el lado interior de la curva y elevación en el exterior)
∙ Vehículo circulando con insuficiencia de peralte I:

(elevación en el lado interior de la curva y descenso en el exterior)
3.11.1.7 Margen perpendicular al plano de rodadura en la zona de ruedas
En la zona de ruedas con el fin de no dificultar el paso de la pestaña (por ejemplo entarimados de pasos a nivel, pasos entre vías, etc), deberá tenerse en cuenta un margen a fin de considerar el desgaste de los carriles.
La zona de ruedas para los gálibos GI1, GI2 y GI3 se define en las figuras 3.28, 3.29 y 3.30.
|
(1) Zona de ruedas (2) Zona de extracción de los calces de frenado a Plano de rodadura b Eje del contorno de referencia cinemático Figura 3.28. Zona de rueda. Gálibo GI1 |
|
(1) Zona de implantación del sistema de repetición de señales (RS, cocodrilos) (2) Zona de ruedas Figura 3.29. Zona de rueda. Gálibo GI2 |
|
(1) Zona de ruedas (2) Zona de implantación del sistema de repetición de señales (RS, cocodrilos) Figura 3.30. Zona de rueda. Gálibo GI3 |
3.11.2 GÁLIBO LÍMITE DE IMPLANTACIÓN DE OBSTÁCULOS
En los cuadros 3.18 y 3.19 se indican las fórmulas a emplear en cada caso y situación, tomadas de las situaciones generalmente más desfavorables del cuadro 3.1siendo:



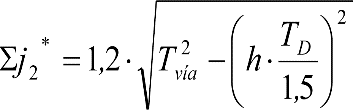
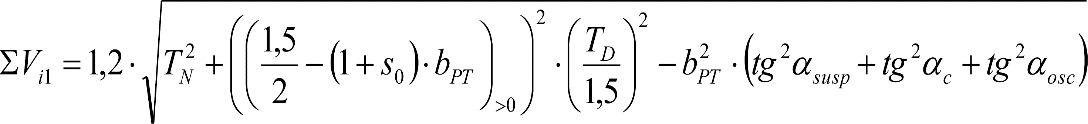
El signo [ ]>0 significa que cuando la expresión entre paréntesis es positiva, mantiene su valor, y cuando es negativa o nula, se toma cero.

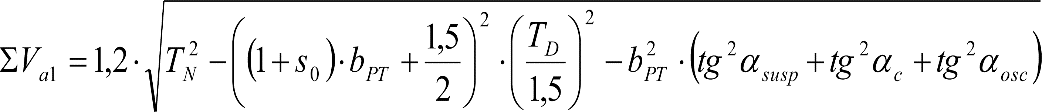
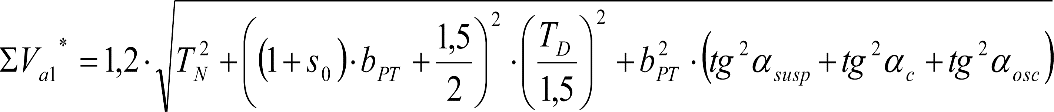
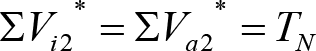
|
V máx (I) |
Punto PT | Lado exterior de la curva | bobstáculo máximo con h obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes bajas (h≤0,4m) | hobstáculo máximo con b obstáculo compatible |
|
||
| Punto PT | Lado interior de la curva | hobstáculo máximo con b obstáculo compatible |
|
|
| Partes altas:puntos por encima de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes bajas (h≤0,4m) | bobstáculo máximo con h obstáculo compatible |
|
||
|
Cuadro 3.18. Fórmulas consideradas con vehículo circulando a V máx (I), correspondientes a las situaciones generalmente más desfavorables |
||||
|
V=0 (D) |
Punto PT | Lado exterior de la curva | hobstáculo máximo con b obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes bajas (h≤0,4m) | bobstáculo máximo con h obstáculo compatible |
|
||
| Punto PT | Lado interior de la curva | bobstáculo máximo con h obstáculo compatible |
|
|
| Partes altas:puntos por encima de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes bajas (h≤0,4m) | hobstáculo máximo con b obstáculo compatible |
|
||
|
Cuadro 3.19. Fórmulas consideradas con vehículo parado (D), correspondientes a las situaciones generalmente más desfavorables |
||||
3.11.3 GÁLIBO NOMINAL DE IMPLANTACIÓN DE OBSTÁCULOS
Los márgenes considerados son los siguientes:
a) Márgenes horizontales
M3b = 0,200 m en los puntos del contorno de referencia con h>0,4m.
M3b = 0,200 m y 0 en h=0,4m. Se produce una discontinuidad en el gálibo nominal.
M3b = 0 en los puntos bajos del contorno de referencia (h<0,4m).
b) Márgenes verticales
M3h = 0,150 m en los puntos del contorno de referencia con h>0,4m.
M3h = 0,150 m y 0 en h=0,4m. Se produce una discontinuidad en el gálibo nominal.
M3h = 0 en los puntos bajos del contorno de referencia (h<0,4m).
En los cuadros 3.20 y 3.21 se indican las fórmulas a emplear en cada caso y situación, tomadas de las situaciones generalmente más desfavorables del cuadro 3.3, siendo:

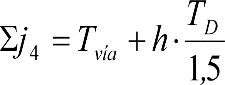
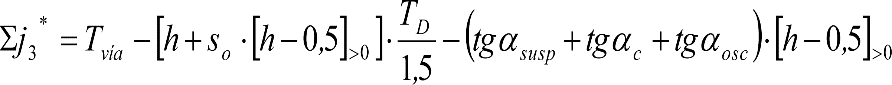

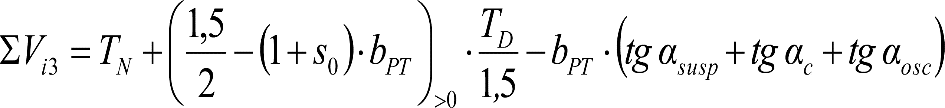

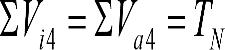
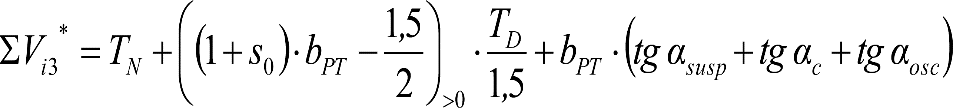

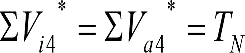
|
V máx (I) |
Punto PT | Lado exterior de la curva | bobstáculo máximo con h obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| h=0,4m | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes bajas (h<0,4m) | hobstáculo máximo con b obstáculo compatible |
|
||
| Punto PT | Lado interior de la curva | hobstáculo máximo con b obstáculo compatible |
|
|
| Partes altas:puntos por encima de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| h=0,4m | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes bajas (h<0,4m) | bobstáculo máximo con h obstáculo compatible |
|
||
|
Cuadro 3.20. Fórmulas consideradas con vehículo circulando a Vmáx (I), correspondientes a las situaciones generalmente más desfavorables |
||||
|
V=0 (D) |
Punto PT | Lado exterior de la curva | hobstáculo máximo con b obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| h=0,4m | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes bajas (h<0,4m) | bobstáculo máximo con h obstáculo compatible |
|
||
| Punto PT | Lado interior de la curva | bobstáculo máximo con h obstáculo compatible |
|
|
| Partes altas:puntos por encima de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes altas:puntos por debajo de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| h=0,4m | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes bajas (h<0,4m) | hobstáculo máximo con b obstáculo compatible |
|
||
|
Cuadro 3.21. Fórmulas consideradas con vehículo parado (D), correspondientes a las situaciones generalmente más desfavorables |
||||
3.11.4 GÁLIBO DEL PANTÓGRAFO
3.11.4.1 Contorno de referencia del pantógrafo
Como contornos de referencia para pantógrafos de 1.950 mm o 1.600 mm de ancho se tomarán los representados en las figuras 3.24 y 3.25 del apartado 3.10.4.1.
3.11.4.2 Valor de los parámetros
∙ Semiancho de la mesilla del pantógrafo (bw): definido en el cuadro 3.5 del apartado 3.5.1.1.
∙ Desplazamientos laterales máximos del pantógrafo:
∙ epo = 0,170 m, a la máxima altura de verificación h’0 = 6,5 m
∙ epu = 0,110 m, a la mínima altura de verificación h’u = 5 m
∙ Salientes: 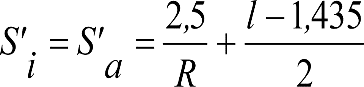
∙ L = 1,500 m
∙ s’0 = 0,225
∙ h’c0 = 0,5 m
∙ D’o = I’o = 1/15 ≈ 0,066 m
∙ Desplazamientos cuasiestáticos horizontales:
∙ Lado interior curva:
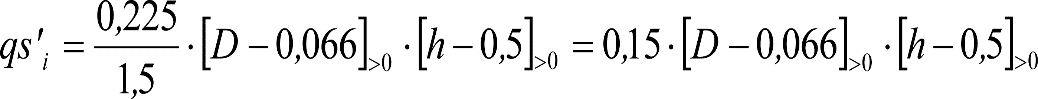
∙ Lado exterior curva:
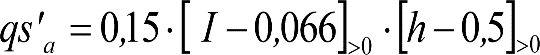
∙ Desplazamientos aleatorios: definidos en el cuadro 3.8 del apartado 3.10.1.3.
Se tomarán los siguientes valores deαosc:
– Para vía en balasto en buen estado: 0,06.º del lado interior de la curva y 0,34.º del lado exterior de la curva.
– Para vía en balasto en mal estado: 0,11.º del lado interior de la curva y 0,6.º del lado exterior de la curva.
– Para vía en placa: 0,06.º del lado interior de la curva y 0,34.º del lado exterior de la curva.
∙ cw = 0,2 (en líneas existentes, para pantógrafos con trocadores aislados).
∙ cw = 0 (en líneas nuevas o acondicionadas, para permitir pantógrafos con trocadores no aislados).
3.11.4.3 Anchura del gálibo mecánico
Se considerarán las siguientes expresiones:
∙ Hacia el interior de la curva:
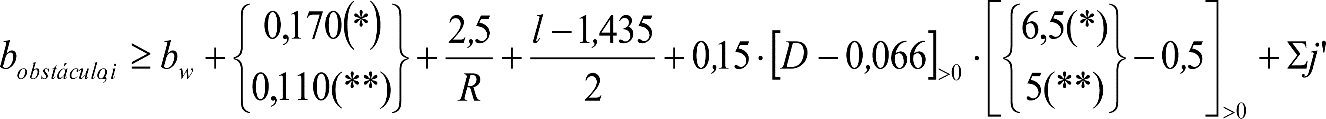
∙ Hacia el exterior de la curva:
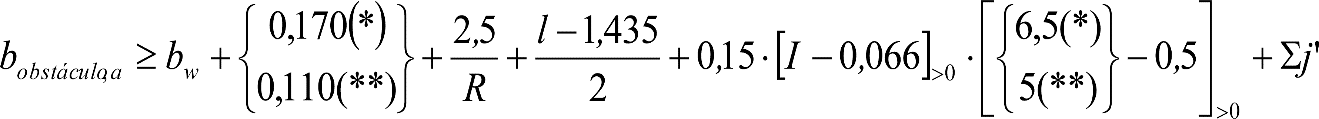
siendo:
bw: semiancho de la mesilla del pantógrafo, definido en el cuadro 3.5 del apartado 3.5.1.1.

(*) Valor a aplicar para la altura máxima de verificación; (**) Valor a aplicar para la altura mínima de verificación. Se interpolará para alturas intermedias.
3.11.4.4 Anchura del gálibo eléctrico
Se obtendrá a partir de las expresiones del apartado 3.5.2.1, particularizando para los valores de bobstáculo obtenidos en el apartado anterior, de belec definida en el cuadro 3.7 del apartado 3.5.2, y de cw = 0,2 (en líneas existentes, para pantógrafos con trocadores aislados) o cw = 0 (en líneas nuevas o acondicionadas, para permitir pantógrafos con trocadores no aislados).
3.11.4.5 Alturas de los gálibos mecánico y eléctrico
Se determinarán según lo indicado en los apartados 3.5.1.3 y 3.5.2.2
3.11.5 DISTANCIA ENTRE EJES DE VÍAS
3.11.5.1 Determinación del entreeje límite
Se obtendrá de la expresión

siendo:
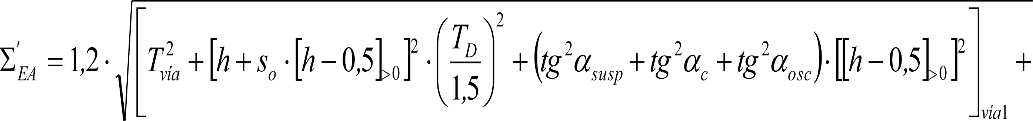
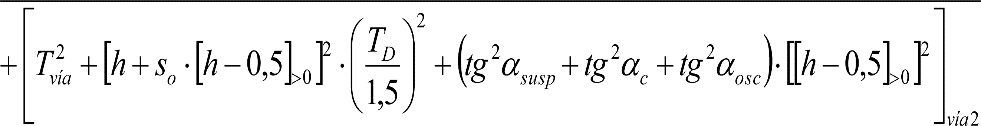
3.11.5.2 Determinación del entreeje nominal
Se considerará lo indicado en el apartado 3.10.5.2.
3.11.6 DISTANCIA ENTRE EJE DE VÍA Y BORDE DE ANDÉN
Bajo las siguientes hipótesis:
∙ Sobreancho máximo: 30 mm
∙ Peralte máximo: D = 0,100 m
∙ Insuficiencia de peralte máxima: Imax = 0,100 m
∙ Vía en balasto, en mal estado.
∙ Cálculos realizados para andén vertical recto, sin bordillo retranqueado.
En los andenes donde no se cumplan las hipótesis anteriores, la determinación de la distancia entre eje de vía y borde de andén requerirá un estudio específico.
| Altura del andén (h q), en mm. | Borde de andén | Radio de la curva (R), en m | |||||
|---|---|---|---|---|---|---|---|
| R ≥ 5000 m | 5000 > R ≥ 1000 m | 1000 > R ≥ 250 m | |||||
| Peralte (D ), en mm | |||||||
| D=0 | D=100 mm | D=0 | D=100 mm | D=0 | D=100 mm | ||
| 760 | Exterior | 1675 | 1675(*) | 1680 | 1680(*) | 1690 | 1690(*) |
| Interior | 1675 | 1720 | 1680 | 1725 | 1690 | 1735 | |
| 680 | Exterior | 1670 | 1670(*) | 1675 | 1675(*) | 1685 | 1685(*) |
| Interior | 1670 | 1715 | 1675 | 1715 | 1685 | 1730 | |
| (*) Para el caso de andén exterior y vía con peralte conviene utilizar el valor correspondiente a vía sin peralte, en previsión de un posible cambio durante la vida de la vía a peralte cero. | |||||||
|
Cuadro 3.22. Distancia de borde de andén a eje de vía (bandén,i/a,lím) |
|||||||
con las tolerancias indicadas en el cuadro 3.23.
|
Actuación en vía |
Tolerancias (mm) | |
|---|---|---|
| h q | T q | |
| Construcción, acondicionamiento o renovación de vía | (0;-10) | 10 |
| Mantenimiento de vía | (0;-30) | 30 |
|
Cuadro 3.23. Tolerancias en andenes |
||
3.11.7 GÁLIBO UNIFORME DE IMPLANTACIÓN DE OBSTÁCULOS
Si se cumplen las siguientes hipótesis:
∙ Radio mínimo en planta: R = 250 m
∙ Radio mínimo de acuerdo vertical: Rv = 2.000 m
∙ Sobreancho máximo: 30 mm
∙ Peralte máximo: D = 0,160 m
∙ Insuficiencia de peralte máxima: Imax = 0,150 m
∙ TN en partes bajas 5 mm.
∙ Vía en balasto, en mal estado.
∙ Catenaria EAC-350.
∙ Pantógrafo con ancho de la mesilla 2xbw=1.950 mm y trocadores no aislados cw=0.
∙ Balizas ASFA situadas en acuerdos verticales de radio superior a 4.000 m y sistemas de señalización mediante ERTMS y LZB con independencia del radio de acuerdos verticales.
los gálibos uniformes GB y GC, serán los definidos en las figuras 3.31 y 3.32. En aquellos puntos donde no se cumplan las hipótesis anteriores, la determinación del gálibo nominal de implantación de obstáculos requerirá un estudio específico.
Los ejes X y Y, son respectivamente, paralelo y perpendicular al plano de rodadura.
|
Figura 3.31. Gálibo uniforme GB |
|
Figura 3.32. Gálibo uniforme GC |
3.11.8 CARACTERÍSTICAS DE LOS VEHÍCULOS DE REFERENCIA
Para el cálculo del gálibo de implantación de obstáculos en las zonas de aparatos de vía o curvas de transición se considerarán los vehículos de referencia definidos en el cuadro 3.24.
| Gálibo |
hmin [mm] |
hmax [mm] |
bCR [mm] |
Ai [m] |
Aa [m] |
B i,a [mm] |
bveh [mm] |
a [m] |
na [m](5 m) | na [m](20 m) |
|---|---|---|---|---|---|---|---|---|---|---|
| GC | 400 | max. | 1 645 | 3,75 | 1 645 | 5,477 | ||||
| GC | 400 | max. | 1 645 | 3,75 | 1 645 | 1,208 | 0,368 | |||
| GC | 400 | max. | 1 645 | 50 | 185 | 1 460 | 20,000 | |||
| GC | 400 | max. | 1 645 | 60 | 225 | 1 420 | 8,736 | 4,832 | ||
| GB | 400 | 3 250 | 1 645 | 3,75 | 1 645 | 5,477 | ||||
|
GB |
400 | 3 250 | 1 645 | 3,75 | 1 645 | 1,208 | 0,368 | |||
|
GB |
400 | 3 250 | 1 645 | 50 | 185 | 1 460 | 20,000 | |||
|
GB |
400 | 3 250 | 1 645 | 60 | 225 | 1 420 | 8,736 | 4,832 | ||
|
GB |
4 110 |
max. | 1 645 | 20 | 1 645 | 12,649 | ||||
| GB |
4 110 |
max. | 1 645 | 20 | 1 645 | 4,301 | 1,832 | |||
| GB |
4 110 |
max. | 1 645 | 50 | 120 | 1 525 | 20,000 | |||
|
GB |
4 110 | max. | 1 645 | 50 | 120 | 1 525 | 7,808 | 4,142 | ||
|
Cuadro 3.24. Características de los vehículos de referencia en los gálibos GB y GC |
||||||||||
3.12 APLICACIÓN A LÍNEAS CON ANCHO MÉTRICO
3.12.1 REGLAS ASOCIADAS
3.12.1.1 Salientes
Se considerarán los salientes Si y Sa recogidos en el apartado 2.9.2.4.
Como ancho de vía, se tomará el valor:
∙ l = lmáx = lN + sobre ancho máximo = lN +0,03 = 1,030m (para cálculo de los gálibos límite, nominal y uniforme de implantación de obstáculos así como para el entreeje límite y nominal).
siendo: lN=1,000m.
3.12.1.2 Desplazamientos cuasiestáticos laterales (solo para h>hco)
Se obtendrán particularizando las fórmulas del apartado 3.2.2.2, para los siguientes valores:
∙ L = 1,055m
∙ D0 = I0 = 0,07m
∙ hco = 0,5m
∙ so = 0,4
Los desplazamientos cuasiestáticos de cualquier punto del vehículo situado a una altura h respecto al plano de rodadura, serán:
∙ Hacia el interior de la curva (puntos del contorno interior y exterior del vehículo):
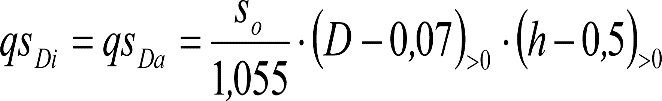
∙ Hacia el exterior de la curva (puntos del contorno interior y exterior del vehículo):
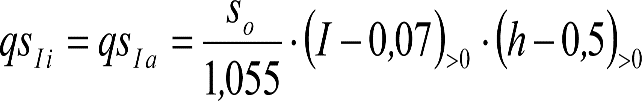
3.12.1.3 Desplazamientos aleatorios laterales y perpendiculares al plano de rodadura
Se obtendrán particularizando las fórmulas de los apartados 3.2.2.3 y 3.2.3.3, con los valores de los parámetros indicados en el cuadro 3.25.
| Parámetros | Símbolo | Vía en balasto | Vía en placa | ||
|---|---|---|---|---|---|
| Interior de la curva | Interior de la curva | Interior de la curva | Exterior de la curva | ||
| Desplazamiento de vía | T vía | 0,025 m | 0,025 m | 0,005 m | 0,005 m |
| Desviación del peralte | T D | 0,020 m | 0,020 m | 0,003 m | 0,003 m |
| Disimetría debida al reparto de cargas | α c | 0,77.º | 0,77.º | 0,77.º | 0,77.º |
| Disimetría debida al reglaje de las suspensiones | α susp | 0,23.º | 0,23.º | 0,23.º | 0,23.º |
| Oscilaciones por irregularidades | α osc (1) | 0,2.º | 1.º | 0,1.º | 0,6.º |
| Desplazamiento vertical de la vía | T N |
Para las partes bajas entre carriles y para aquellos obstáculos que se muevan solidariamente con la vía: 5 mm. En el caso de obstáculos que no se muevan solidariamente con la vía: 20 mm |
|||
| Factor de seguridad para la determinación del gálibo límite de implantación de obstáculos | K |
1,2 en general 1 (en el caso de los desplazamientos aleatorios laterales para h<0,5m) |
|||
| Factor de seguridad para la determinación del gálibo mecánico del pantógrafo | K’ |
1 |
|||
|
(1) Nota: Los valores de αosc indicados se utilizarán para el cálculo de los desplazamientos laterales. En el caso de los desplazamientos verticales se tomarán del lado interior de la curva los valores del lado exterior de la curva y del lado exterior de la curva los valores del lado interior de la curva. |
|||||
|
Cuadro 3.25. Parámetros para el cálculo de los desplazamientos aleatorios en los gálibos GEE10 y GED10 |
|||||
3.12.1.4 Márgenes complementarios laterales (M3b) y verticales (M3h)
Se consideran los siguientes valores:
∙ Márgenes horizontales (M3b):
– 0,200 m para los puntos con h>0,4m.
– 0,200 m y 0 para h=0,4 m. En este punto se produce una discontinuidad en el gálibo nominal
– 0 para puntos con h<0,4 m.
∙ Márgenes verticales (M3h):
– 0,150 m para los puntos con h>0,4m.
– 0,150 m y 0 para h=0,4 m. En este punto se produce una discontinuidad en el gálibo nominal
– 0 para puntos con h<0,4 m.
3.12.1.5 Inscripción en acuerdos verticales
El radio del acuerdo vertical Rv≥500m.
– Las cotas verticales de los puntos ![]() del contorno de referencia por encima de la anchura máxima se aumentarán en
del contorno de referencia por encima de la anchura máxima se aumentarán en 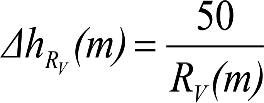 y los puntos del contorno de referencia por debajo de la anchura máxima se reducirán en
y los puntos del contorno de referencia por debajo de la anchura máxima se reducirán en 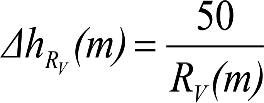
– Las cotas verticales de las partes bajas, fuera de la zona de ruedas, del contorno de referencia se reducirán en el mismo valor. En el caso de 500 m ≤ Rv ≤ 625 m y para cotas iguales o inferiores a 80 mm, como las reducciones serían mayores que la altura del contorno de referencia, solo se considerará una reducción igual a la distancia entre el contorno de referencia y el plano de rodadura.
3.12.1.6 Desplazamientos cuasiestáticos perpendiculares al plano de rodadura
Se obtendrán particularizando las fórmulas del apartado 3.2.3.2, para los siguientes valores:
∙ L=1,055m
∙ D0 = I0 = 0,07m
∙ hco=0,5m
∙ so = 0,4
Los desplazamientos cuasiestáticos verticales causados por D e I, para los puntos PT, situado a una altura hPT respecto al plano de rodadura y a una distancia horizontal bPT respecto al eje de la vía, serán:
∙ Vehículo parado con peralte D:
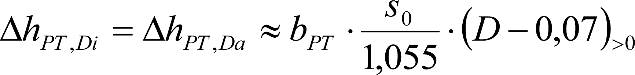
(descenso en el lado interior de la curva y elevación en el exterior)
∙ Vehículo circulando con insuficiencia de peralte I:

(elevación en el lado interior de la curva y descenso en el exterior)
3.12.1.7 Margen perpendicular al plano de rodadura en la zona de ruedas
En la zona de ruedas con el fin de no dificultar el paso de la pestaña (por ejemplo entarimados de pasos a nivel, pasos entre vías, etc), deberá tenerse en cuenta un margen a fin de considerar el desgaste de los carriles.
La zona de ruedas queda delimitada por los puntos del contorno de referencia situados en el intervalo 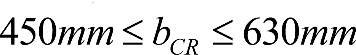
|
l : Ancho de vía Figura 3.33. Zona de ruedas de los gálibos GEE10 y GED10 |
3.12.2 GÁLIBO LÍMITE DE IMPLANTACIÓN DE OBSTÁCULOS
En los cuadros 3.26 y 3.27 se indican las fórmulas a emplear en cada caso y situación, tomadas de las situaciones generalmente más desfavorables del cuadro 3.1 siendo:
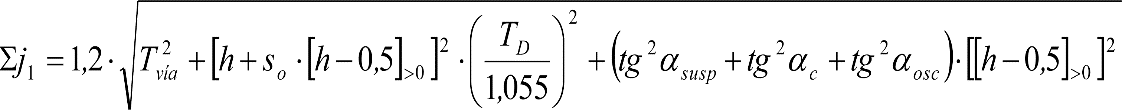
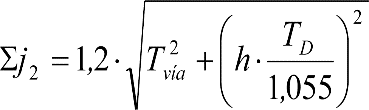

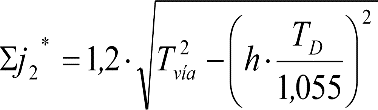
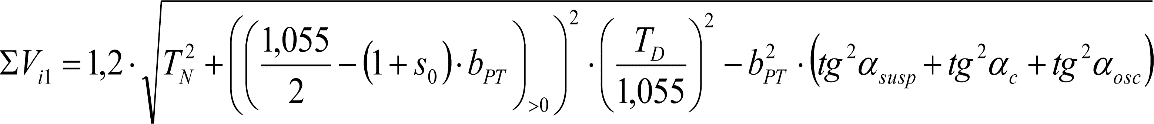
El signo [ ]>0 significa que cuando la expresión entre paréntesis es positiva, mantiene su valor, y cuando es negativa o nula, se toma cero.
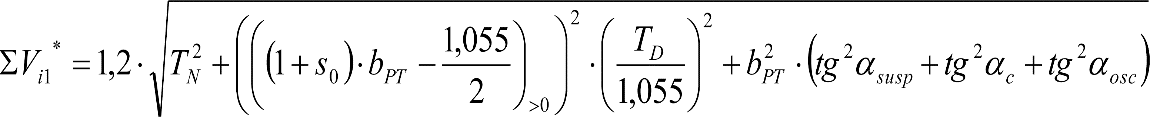
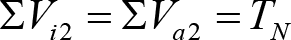
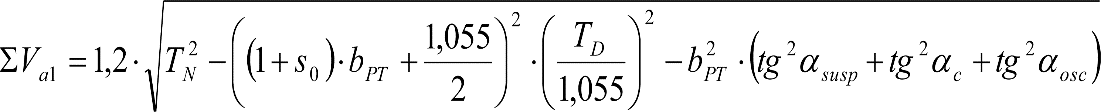
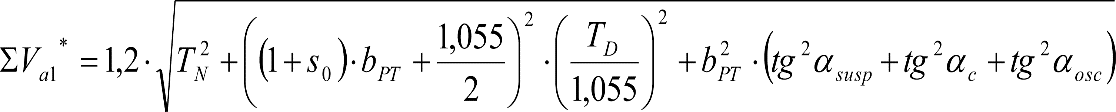
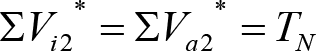
|
V máx (I) |
Punto PT | Lado exterior de la curva | bobstáculo máximo con h obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes bajas (h≤0,4m) | hobstáculo máximo con b obstáculo compatible |
|
||
| Punto PT | Lado interior de la curva | hobstáculo máximo con b obstáculo compatible |
|
|
| Partes altas:puntos por encima de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes bajas (h≤0,4m) | bobstáculo máximo con h obstáculo compatible |
|
||
|
Cuadro 3.26 Fórmulas consideradas con vehículo circulando a Vmáx (I), correspondientes a las situaciones generalmente más desfavorables |
||||
|
V=0 (D) |
Punto PT | Lado exterior de la curva | hobstáculo máximo con b obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes bajas (h≤0,4m) | bobstáculo máximo con h obstáculo compatible |
|
||
| Punto PT | Lado interior de la curva | bobstáculo máximo con h obstáculo compatible |
|
|
| Partes altas:puntos por encima de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes bajas (h≤0,4m) | hobstáculo máximo con b obstáculo compatible |
|
||
|
Cuadro 3.27. Fórmulas consideradas con vehículo parado (D), correspondientes a las situaciones generalmente más desfavorables |
||||
3.12.3 GÁLIBO NOMINAL DE IMPLANTACIÓN DE OBSTÁCULOS
Los márgenes considerados son los siguientes:
a) Márgenes horizontales
M3b = 0,200 m en los puntos del contorno de referencia con h>0,4m.
M3b = 0,200 m y 0 en h=0,4m. Se produce una discontinuidad en el gálibo nominal.
M3b = 0 en los puntos bajos del contorno de referencia (h<0,4m).
b) Márgenes verticales
M3h = 0,150 m en los puntos del contorno de referencia con h>0,4m.
M3h = 0,150 m y 0 en h=0,4m. Se produce una discontinuidad en el gálibo nominal.
M3h = 0 en los puntos bajos del contorno de referencia (h<0,4m).
En los cuadros 3.28 y 3.29 se indican las fórmulas a emplear en cada caso y situación, tomadas de las situaciones generalmente más desfavorables del cuadro 3.3 siendo:
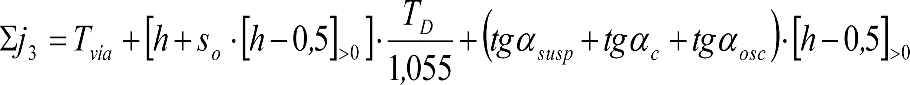
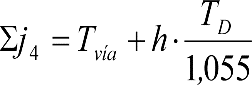





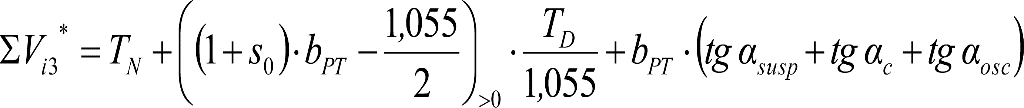


|
V máx (I) |
Punto PT | Lado exterior de la curva | bobstáculo máximo con h obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| h=0,4m | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes bajas (h<0,4m) | hobstáculo máximo con b obstáculo compatible |
|
||
|
V máx (I) |
Punto PT | Lado interior de la curva | hobstáculo máximo con b obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| h=0,4m | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes bajas (h<0,4m) | bobstáculo máximo con h obstáculo compatible |
|
||
|
Cuadro 3.28. Fórmulas consideradas con vehículo circulando a Vmáx (I), correspondientes a las situaciones generalmente más desfavorables |
||||
|
V=0 (D) |
Punto PT | Lado exterior de la curva | hobstáculo máximo con b obstáculo compatible |
|
| Partes altas:puntos por encima de la anchura máxima | hobstáculo máximo con b obstáculo compatible |
|
||
| h=0,4m | bobstáculo máximo con h obstáculo compatible |
|
||
| Partes bajas (h<0,4m) | bobstáculo máximo con h obstáculo compatible |
|
||
| Punto PT | Lado interior de la curva | bobstáculo máximo con h obstáculo compatible |
|
|
| Partes altas:puntos por encima de la anchura máxima | bobstáculo máximo con h obstáculo compatible |
|
||
| h=0,4m | hobstáculo máximo con b obstáculo compatible |
|
||
| Partes bajas (h<0,4m) | hobstáculo máximo con b obstáculo compatible |
|
||
|
Cuadro 3.29. Fórmulas consideradas con vehículo parado (D), correspondientes a las situaciones generalmente más desfavorables |
||||
3.12.4 GÁLIBO DEL PANTÓGRAFO
3.12.4.1 Contorno de referencia del pantógrafo
Como contorno de referencia para pantógrafo de 1.700 mm de ancho se tomará el representado en la figura 3.34.
|
Figura 3.34. Contorno de referencia para pantógrafos de 1.700 mm de ancho en posición de captación. Gálibo GEE10 |
3.12.4.2 Valor de los parámetros
∙ Semiancho de la mesilla del pantógrafo (bw): definido en el cuadro 3.5 del apartado 3.5.1.1.
∙ Desplazamientos laterales máximos del pantógrafo:
∙ epo = 0,150 m, a la máxima altura de verificación h’0 = 5,5 m
∙ epu = 0,082 m, a la mínima altura de verificación h’u = 4,3 m
∙ Salientes: 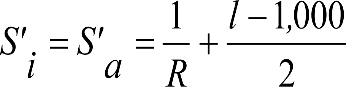
∙ L = 1,055 m
∙ s’0 = 0,225
∙ h’c0 = 0,5 m
∙ D’o = I’o = 0,07 m
∙ Desplazamientos cuasiestáticos horizontales:
∙ Lado interior curva:
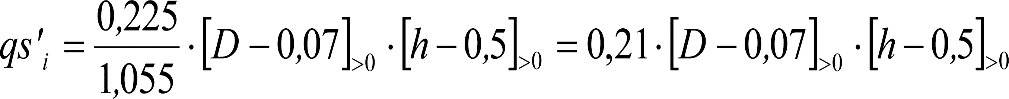
∙ Lado exterior curva:
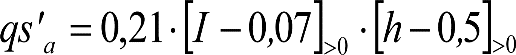
∙ Desplazamientos aleatorios: definidos en el cuadro 3.25 del apartado 3.12.1.3.
Se tomarán los siguientes valores de αosc:
– Para vía en balasto: 0,11º del lado interior de la curva y 0,60º del lado exterior de la curva.
– Para vía en placa: 0,06º del lado interior de la curva y 0,34º del lado exterior de la curva.
∙ cw = 0
3.12.4.3 Anchura del gálibo mecánico
Se considerarán las siguientes expresiones:
∙ Hacia el interior de la curva:
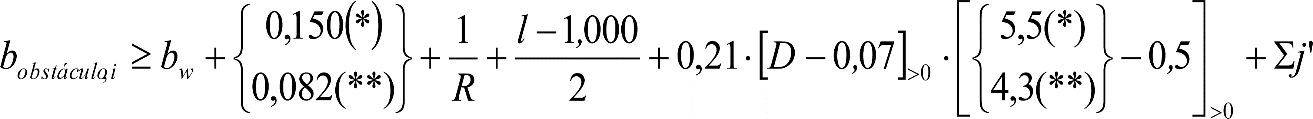
∙ Hacia el exterior de la curva:

siendo:
bw: semiancho de la mesilla del pantógrafo, definido en el cuadro 3.5 del apartado 3.5.1.1.
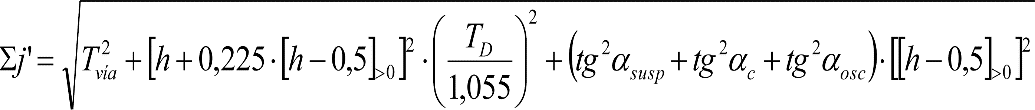
(*) Valor a aplicar para la altura máxima de verificación; (**) Valor a aplicar para la altura mínima de verificación. Se interpolará para alturas intermedias.
3.12.4.4 Anchura del gálibo eléctrico
Se obtendrá a partir de las expresiones del apartado 3.5.2.1, particularizando para los valores de bobstáculo obtenidos en el apartado anterior, de belec definida en el cuadro 3.7 del apartado 3.5.2, y de cw = 0.
3.12.4.5 Alturas de los gálibos mecánico y eléctrico
Se determinarán según lo indicado en los apartados 3.5.1.3 y 3.5.2.2
3.12.5 DISTANCIA ENTRE EJES DE VÍAS
3.12.5.1 Determinación del entreeje límite
Se obtendrá de la expresión
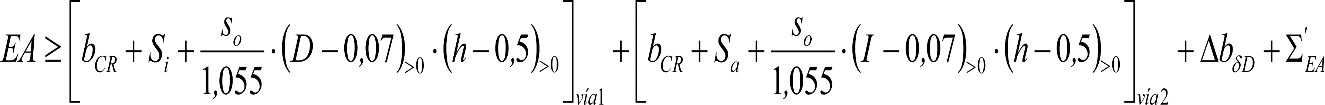
siendo:

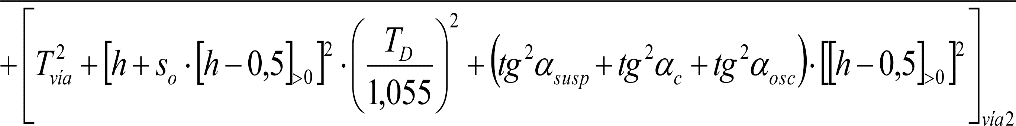
3.12.5.2 Determinación del entreeje nominal
La distancia nominal entre ejes de vías será de 3,5 m.
3.12.6 DISTANCIA ENTRE EJE DE VÍA Y BORDE DE ANDÉN
Punto abierto (pendiente de estudio).
3.12.7 GÁLIBO UNIFORME DE IMPLANTACIÓN DE OBSTÁCULOS
Si se cumplen las siguientes hipótesis:
∙ Radio mínimo en planta: R = 100 m
∙ Radio mínimo de acuerdo vertical: Rv = 2.000 m
∙ Sobreancho máximo: 30 mm
∙ Peralte máximo: D = 0,110 m
∙ Insuficiencia de peralte máxima: Imax = 0,070 m
∙ TN en partes bajas: 5 mm.
∙ Vía en balasto.
∙ Catenaria CA-160.
∙ Pantógrafo con ancho de la mesilla 2xbw=1.700 mm y trocadores no aislados cw=0.
∙ Balizas ASFA situadas en acuerdos verticales de radio superior a 4.000 m.
Los gálibos uniformes GEE10 y GED10, serán los definidos en las figuras 3.35 y 3.36. En aquellos puntos donde no se cumplan las hipótesis anteriores, la determinación del gálibo nominal de implantación de obstáculos requerirá un estudio específico.
Los ejes X y Y, son respectivamente, paralelo y perpendicular al plano de rodadura.
|
Figura 3.35. Gálibo uniforme de implantación de obstáculos GEE10 |
|
Figura 3.36. Gálibo uniforme de implantación de obstáculos GED10 |
3.12.8 CARACTERÍSTICAS DE LOS VEHÍCULOS DE REFERENCIA
Para el cálculo del gálibo de implantación de obstáculos en las zonas de aparatos de vía o curvas de transición se considerarán los vehículos de referencia definidos en el cuadro 3.30.
| Gálibo |
hmin [mm] |
hmax [mm] |
bCR [mm] |
Ai [m] |
Aa [m] |
B i,a [mm] |
bveh [mm] |
a [m] |
na [m](5 m) | na [m](20 m) |
|---|---|---|---|---|---|---|---|---|---|---|
| GEE10/GED10 | 400 | max. | 1 530 | 1,5 | 1 530 | 3,464 | ||||
| GEE10/GED10 | 400 | max. | 1 530 | 1,5 | 1 530 | 0,541 | 0,149 | |||
| GEE10/GED10 | 400 | max. | 1 530 | 20 | 185 | 1 345 | 12,649 | |||
| GEE10/GED10 | 400 | max. | 1 530 | 24 | 225 | 1 305 | 4,865 | 2,166 | ||
|
Cuadro 3.30. Características de los vehículos de referencia en los gálibos GEE10 y GED10 |
||||||||||
4.1 CONSIDERACIONES GENERALES
El gálibo de cargamento se obtendrá a partir de los contornos de referencia estáticos definidos en los apartados 4.4.1, 4.5.1 y 4.6.1 y de las reglas asociadas del gálibo estático del apartado 4.2, excepto las que se indiquen de modo expreso.
El contorno resultante define el espacio que no deberá ser rebasado en condiciones estáticas por el cargamento de un vagón.
Cada uno de los contornos de los gálibos de cargamento se obtiene a partir de la cota de 145 mm, en el caso de los gálibos GHE16, GEA16, GEB16, GEC16, GA, GB y GC, y de 165 mm, en el caso de los gálibos GEE10 y GED10, sobre el plano de rodadura, de los contornos de referencia del gálibo estático. En caso de ser necesario usar alturas por debajo de 145 mm (gálibos GHE16, GEA16, GEB16, GEC16, GA, GB y GC) o de 165 mm (gálibos GEE10 y GED10), se utilizará para su estudio el gálibo estático.
4.2 REGLAS ASOCIADAS
Consisten en un conjunto de reducciones y ampliaciones a aplicar al contorno de referencia, que tienen en cuenta posibles desplazamientos del cargamento, respecto a su posición media, debidos a: holguras, inscripciones en curva, etc.
4.2.1 REDUCCIONES Y AMPLIACIONES A CONSIDERAR
Las reducciones y ampliaciones a considerar en la modificación del contorno de referencia serán las siguientes:
1. Reducciones del semiancho del contorno de referencia (bCRst), para considerar los posibles desplazamientos estáticos laterales (Dplst) debidos a:
a) Desplazamientos geométricos (dg) por inscripción en curva, entre el eje de simetría del vehículo y el de la vía.
b) Holguras laterales entre eje de ruedas y vía (wv).
c) Holguras laterales entre eje de ruedas y bastidor de bogie o entre eje de ruedas y caja, en vehículos sin bogie (q).
d) Holguras laterales entre bastidor de bogie y caja (w).
2. Reducciones verticales en las partes inferior y superior del contorno de referencia, para considerar posibles desplazamientos verticales debidos a:
a) Desgastes de los elementos de rodadura del vehículo.
b) Deformaciones de la estructura del vehículo.
c) Efecto de la suspensión.
No se considera la extensión de las suspensiones, al existir un margen de 30 mm entre los contornos de referencia estáticos y cinemáticos de los gálibos GHE16, GEA16, GEB16, GA, GB, GEE10 y GED10 y de 50 mm en los gálibos GEC16 y GC.
Los órganos no suspendidos, debido a que no se ven sometidos a oscilaciones y flexiones, pueden rebasar el contorno de referencia hacia abajo en 15 mm.
d) Inscripción del vehículo en acuerdos verticales.
Estas reducciones verticales, a considerar a efectos de gálibo estático, no son de aplicación al cálculo del gálibo de cargamento.
3. Ampliación del semiancho del contorno de referencia con los «salientes» (Sst) indicados en los apartados 4.4.2.2, 4.5.2.2 y 4.6.2.2, en función del radio de curva de inscripción del vehículo (R) y del ancho de vía (l).
4.2.2 DESPLAZAMIENTOS HORIZONTALES
4.2.2.1 Desplazamiento geométrico (dg) por inscripción en curva
El desplazamiento horizontal, en una curva de radio R, entre los ejes de simetría del vehículo y de la vía, varía con la sección transversal del conjunto vehículo-cargamento considerada, por lo que se calculará en las secciones más desfavorables. Para ello se aplicará lo indicado en el apartado 2.2.3.1.
4.2.2.2 Holguras laterales
En este apartado se definen las holguras laterales de los elementos del vehículo que ponen en contacto la caja con la vía.
4.2.2.2.1 Holgura lateral entre eje de ruedas y vía (w v )
La holgura lateral entre eje de ruedas y vía, a cada lado del vehículo, respecto a su posición media, será:

siendo:
l: ancho de vía. Se tomará: l = lmáx = lN + 0,03.
d: distancia mínima entre las caras activas de las pestañas de las ruedas de un eje, medida a 10 mm por debajo del círculo de rodadura, con ambas pestañas al límite de desgaste.
4.2.2.2.2 Holgura lateral entre eje de ruedas y bastidor del bogie o entre eje y caja, en vehículos sin bogies (q)
La holgura lateral q entre eje de ruedas y bastidor del bogie será la suma de las holguras entre eje y caja de grasa, y entre ésta y las placas de guarda o el bastidor del bogie, medidas a partir de su posición media y a cada lado, con todos los elementos al límite de desgaste.
En vehículos sin bogies esta holgura se da entre el eje y la caja del vehículo.
4.2.2.2.3 Holgura lateral entre bastidor del bogie y caja (w)
Esta holgura se da entre la estructura soporte de los elementos de rodadura (bogie, rodal, etc.) y la caja del vehículo.
En los vehículos convencionales esta holgura se produce entre los pivotes de los bogies y las vigas bailadoras. Para vehículos sin pivote, es la holgura de la caja respecto al bastidor del bogie. Se mide desde la posición media y a cada lado.
Se considerará un valor de w constante.
4.2.2.2.4 Posición de rodadura del vehículo sobre la vía y factores de desplazamiento (A)
Los factores de desplazamiento a considerar serán los definidos en el cuadro 2.4, caso 2, definido en el apartado 2.2.3.2.4.
4.3 CÁLCULO DEL GÁLIBO DE CARGAMENTO
El semiancho del cargamento (bcarg) se obtendrá añadiendo al contorno de referencia estático (bCRst) el correspondiente saliente estático (Sst) y restando los desplazamientos estáticos (Dplst).

A fin de que no se produzcan interferencias entre el cargamento y los obstáculos se debe verificar la siguiente relación entre el contorno de referencia cinemático (bCR) y estático (bCRst):
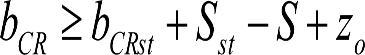
(5)
(5) Esta relación no se cumple para el gálibo histórico GHE16 en alturas comprendidas entre 400 y 600 mm sobre el plano de rodadura.
siendo:
S: Saliente cinemático.
zo: Desplazamiento fijo a considerar para tener en cuenta los desplazamientos cuasiestáticos admisibles del vehículo.

siendo:
slimite: Coeficiente de flexibilidad admisible del vagón más el cargamento.
Es decir:  y
y 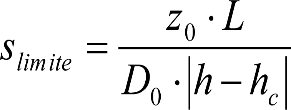
Por tanto deberá verificarse que la flexibilidad del vagón más el cargamento no excede de slimite cuyos valores se definen en el apartado 4.4.2.3 (GHE16, GEA16, GEB16 y GEC16), 4.5.2.3 (GA, GB y GC) y 4.6.2.3 (GEE10 y GED10). Cuando se exceda el valor de slimite deberá aplicarse el gálibo de material rodante definido en el capítulo 2.
La consideración de los desplazamientos horizontales del apartado 4.2.2, junto con el saliente correspondiente, permite calcular la reducción del semiancho del contorno de referencia, a fin de obtener el gálibo de cargamento.
Las reducciones del semiancho del contorno de referencia en secciones internas (Ei) y externas (Ea) serán, respectivamente:
 ,
,
siendo:
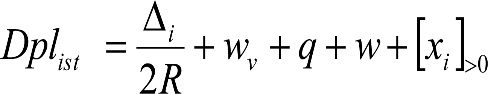
 ,
,
siendo:

donde:
Sist: y Sast: Salientes estáticos en secciones internas y externas, respectivamente.
En el anejo 11 se incluyen algunos ejemplos de aplicación de las fórmulas de reducción.
4.4 APLICACIÓN A LÍNEAS CON ANCHO IBÉRICO
4.4.1 CONTORNOS DE REFERENCIA
Se consideran los siguientes contornos de referencia en las partes altas:
∙ GHE16
∙ GEA16
∙ GEB16
∙ GEC16
Se considera el siguiente contorno de referencia en las partes bajas:
∙ GEI1: material rodante apto para circular por vías equipadas con frenos de vía en posición activa y lomos de asno de las estaciones de clasificación.
Las dimensiones detalladas de cada contorno de referencia del Gálibo de Cargamento, a partir de una altura de 430 mm sobre carril, por alturas escalonadas cada 10 mm, se recogen en el anejo 8.
4.4.1.1 Contorno de referencia de las partes altas
4.4.1.1.1 GHE16
El contorno de referencia de las partes altas se define en la figura 4.1.
|
(1) Plano de rodadura NOTA Partes bajas definidas en la figura 4.5 |
|
Figura 4.1. Contorno de referencia del gálibo estático GHE16. Partes altas |
4.4.1.1.2 GEA16
Este contorno es una envolvente de los contornos GHE16 y GA (definido en la norma EN15273-2:2.013).
La figura 4.2 define el contorno de referencia para las partes altas.
|
(1) Plano de rodadura NOTE Partes bajas definidas en la figura 4.5 |
|
Figura 4.2. Contornos de referencia del gálibo estático GEA16. Partes altas |
4.4.1.1.3 GEB16
Este contorno es una envolvente de los contornos GHE16 y GB (definido en la norma EN15273-2:2.013).
La figura 4.3 define el contorno de referencia para las partes altas.
|
(1) Plano de rodadura NOTE Partes bajas definidas en la figura 4.5 |
|
Figura 4.3. Contornos de referencia del gálibo estático GEB16. Partes altas |
4.4.1.1.4 GEC16
Este contorno es una envolvente de los contornos GHE16 y GC (definido en la norma EN15273-2:2.013).
La figura 4.4 define el contorno de referencia para las partes altas.
|
(1) Plano de rodadura NOTA Partes bajas definidas en la figura 4.5 |
|
Figura 4.4. Contornos de referencia del gálibo estático GEC16. Partes altas |
4.4.1.2 Contorno de referencia de las partes bajas GEI1
La figura 4.5 define el contorno de referencia del gálibo estático GEI1.
Para alturas inferiores a 145 mm, sobre el plano de rodadura, las cotas del contorno de referencia estático son las del cinemático incrementadas en 15 mm.
|
(1) Plano de rodadura l: Ancho de vía Figura 4.5. Contorno de referencia del gálibo estático GEI1. Partes bajas |
4.4.2 REGLAS ASOCIADAS
4.4.2.1 holguras laterales
De la expresión del apartado 4.2.2.2.1, se tiene:

siendo:
l: ancho de vía. Se toma: l= lmáx = lN + 0,03 = 1,698m.
d = 1,643 m
El valor de q+w dependerá del tipo de material rodante, pudiendo tomarse como referencia un valor de 0,023 m.
4.4.2.2 Salientes
Se adoptarán los salientes indicados en el cuadro 4.1 en función del gálibo.
Como valor de k se tomará el indicado en el cuadro 4.2 en función del gálibo.
El saliente de las partes altas es igual al indicado en el cuadro 2.7 añadiendo 0,045 m. El saliente de las partes bajas es igual al indicado en el cuadro 2.8 para los gálibos GEI1 y GEI2.
| Salientes máximos para un ancho de vía l y para una altura h del punto considerado sobre el plano de rodadura | ||||||||
|---|---|---|---|---|---|---|---|---|
| Gálibo | Radio | h ≤ 0,43 m | h > 0,43m | |||||
| 0,43 m < h ≤ 3,29 m | h > 3,29 m | |||||||
|
GHE16 GEC16 |
250 ≤ R ≤ ∞ |
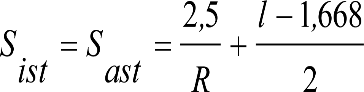
|

|
|||||
| 150 ≤ R < 250 |
|
|
||||||
|
GEA16 GEB16 |
250 ≤ R ≤ ∞ |

|
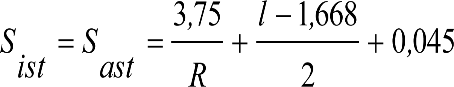
|

|
||||
| 150 ≤ R < 250 |
|
|
|
|||||
| NOTA: S ist = Lado interior de la curva (m); S ast = Lado exterior de la curva (m) | ||||||||
|
Cuadro 4.1. Salientes de los gálibos GHE16, GEA16, GEB16 y GEC16 |
||||||||
| GÁLIBO | Altura h (m) | k |
|---|---|---|
| GHE16 | Cualquier altura | 0 |
| GEC16 | Cualquier altura | 0 |
| GEA16 | h ≤ 3,29 | 0 |
| 3,29 < h < 3,67 |
|
|
| h ≥ 3,67 | 1 | |
| GEB16 | h ≤ 3,29 | 0 |
| 3,29 < h < 4,08 |
|
|
| h ≥ 4,08 | 1 | |
|
Cuadro 4.2. Valor de k para los gálibos GHE16, GEA16, GEB16 y GEC16 |
||
4.4.2.3 Desplazamientos cuasiestáticos
El valor de slimite será de 0,3 para los gálibos GHE16, GEA16, GEB16 y GEC16.
4.4.3 CÁLCULO DEL GÁLIBO DE CARGAMENTO
4.4.3.1 Fórmulas de reducción para los gálibos GHE16 y GEC16
a) Reducción en secciones internas Eist
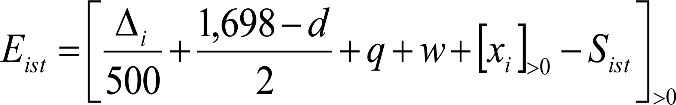
Como las holguras son constantes, las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=250 ó 150 m).
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||
|
|
||
| (1) valor a aplicar en E ist de partes bajas (h ≤ 0,430 m) | (2) valor a aplicar en E ist de partes altas (h > 0,430 m) | |
|
Si: |
||
|
|
||
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
||
| (1) valor a aplicar en E ist de partes bajas (h ≤ 0,430 m) | (2) valor a aplicar en E ist de partes altas (h > 0,430 m) | |
b) Reducción en secciones externas East

Análogamente, como las holguras son constantes, las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=250 ó 150 m).
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
|||
|
|
|||
| (1) valor a aplicar en E ast de partes bajas (h ≤ 0,430 m) | (2) valor a aplicar en E ast de partes altas (h > 0,430 m) | ||
|
Si: |
|||
|
|
|||
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
|||
| (1) valor a aplicar en E ast de partes bajas (h ≤ 0,430 m) | (2) valor a aplicar en E ast de partes altas (h > 0,430 m) | ||
4.4.3.2 Fórmulas de reducción para los gálibos GEA16 y GEB16
Para h ≤ 3,29 m, los valores de Eist y East coinciden con los definidos en el apartado 4.4.3.1.
Para h> 3,29 m las fórmulas de reducción son las siguientes:
Como las holguras son constantes, las máximas reducciones internas y externas se dan para el radio máximo (R=∞) o para el mínimo (R=250 ó 150 m).
a) Reducción en secciones internas Eist

Si: 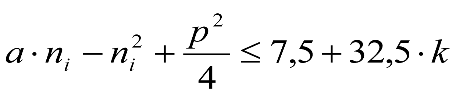 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
|
|
|
Si: |
|
|
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
b) Reducción en secciones externas East
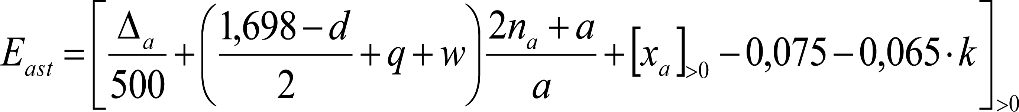
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
|
|
|
|
|
Si: |
|
|
|
|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
|
4.5 APLICACIÓN A LÍNEAS CON ANCHO estándar europeo
4.5.1 CONTORNOS DE REFERENCIA
Se consideran los siguientes contornos de referencia en las partes altas:
∙ GA
∙ GB
∙ GC
Se consideran los siguientes contornos de referencia en las partes bajas:
∙ GI1: material rodante apto para circular por vías equipadas con frenos de vía en posición activa y lomos de asno de las estaciones de clasificación.
∙ GI2: material rodante no apto para circular por vías equipadas con frenos de vía en posición activa ni lomos de asno de las estaciones de clasificación.
Los vehículos motores de maniobras utilizados en las estaciones de clasificación podrán tener el gálibo GI2 si van a pasar por los lomos de asno con los frenos de vía en posición no activa.
Las dimensiones detalladas de cada contorno de referencia del Gálibo de Cargamento, a partir de una altura de 430 mm sobre carril, por secciones escalonadas cada 10 mm, se recogen en el anejo 8.
4.5.1.1 Contorno de referencia de las partes altas
El contorno de referencia de las partes altas de los gálibos GA, GB y GC se define en la figura 4.6.
|
Figura 4.6. Contornos de referencia de los gálibos estáticos GA, GB y GC. Partes altas |
4.5.1.2 Contorno de referencia de las partes bajas
4.5.1.2.1 GI1
La figura 4.7 define el contorno de referencia del gálibo estático GI1.
Para alturas inferiores a 145 mm, sobre el plano de rodadura, las cotas del contorno de referencia estático son las del cinemático incrementadas en 15 mm.
|
(1) Plano de rodadura (2) Eje de simetría del contorno de referencia (3) Posición límite efectiva de la cara exterior de la rueda (4) Anchura máxima teórica del perfil de la pestaña, considerando la posible oblicuidad del eje en la vía. (5) Posición límite efectiva de la cara interna de la rueda, cuando el eje se empuja contra el carril opuesto (6) Estos valores pueden disminuirse 15 mm para las partes no suspendidas. Los órganos así definidos pueden, para una distancia de hasta 950 mm del eje del vehículo, interferir con la zona de extracción de los calces de frenado normalizados (ver zona c del contorno de referencia del gálibo cinemático GI1) Figura 4.7. Contorno de referencia del gálibo estático GI1. Partes bajas |
4.5.1.2.2 GI2
La figura 4.8 define el contorno de referencia del gálibo estático GI2.
|
(1) Plano de rodadura (2) Eje de simetría del contorno de referencia (3) Posición límite efectiva de la cara exterior de la rueda (4) Anchura máxima teórica del perfil de la pestaña, considerando la posible oblicuidad del eje en la vía (5) Posición límite efectiva de la cara interna de la rueda, cuando el eje se empuja contra el carril opuesto (6) Estos valores pueden disminuirse 15 mm para las partes no suspendidas Figura 4.8. Contorno de referencia del gálibo estático GI2. Partes bajas |
4.5.2 REGLAS ASOCIADAS
4.5.2.1 holguras laterales
De la expresión del apartado 4.2.2.2.1, se tiene:

siendo:
l: ancho de vía. Se toma: l = lmáx = lN + 0,03 = 1,465m.
d = 1,410 m
El valor de q+w dependerá del tipo de material rodante, pudiendo tomarse como referencia un valor de 0,023 m.
4.5.2.2 Salientes
Se adoptarán los salientes indicados en el cuadro 4.3 en función del gálibo.
Como valor de k se tomará el indicado en el cuadro 4.4 en función del gálibo.
El saliente de las partes altas es igual al indicado en el cuadro 2.14 añadiendo 0,045 m. El saliente de las partes bajas es igual al indicado en el cuadro 2.15 para los gálibos GI1 y GI2.
| Salientes máximos para un ancho de vía l y para una altura h del punto considerado sobre el plano de rodadura | ||||
|---|---|---|---|---|
| Gálibo | Radio | h ≤ 0,43 m | h > 0,43m | |
| 0,43 m < h ≤ 3,22 m | h > 3,22 m | |||
| GC | 250 ≤ R ≤ ∞ |

|

|
|
| 150 ≤ R < 250 |
|
|
||
|
GA GB |
250 ≤ R ≤ ∞ |
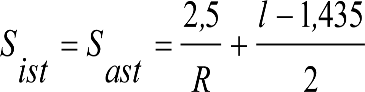
|
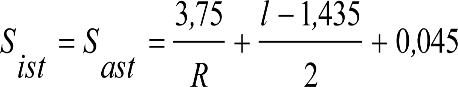
|

|
| 150 ≤ R < 250 |
|
|
|
|
|
NOTA: Sist = Lado interior de la curva (m); Sast = Lado exterior de la curva (m) |
||||
|
Cuadro 4.3. Salientes de los gálibos GA, GB y GC |
||||
|
GÁLIBO |
Altura h (m) | k |
|---|---|---|
| GC | Cualquier altura | 0 |
| GA | h ≤ 3,22 | 0 |
| 3,22 < h < 3,85 |
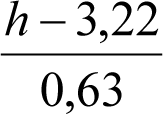
|
|
| h ≥ 3,85 | 1 | |
| GB | h ≤ 3,22 | 0 |
| 3,22 < h < 4,08 |
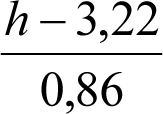
|
|
| h ≥ 4,08 | 1 | |
|
Cuadro 4.4. Valor de k para los gálibos GA, GB y GC |
||
4.5.2.3 Desplazamientos cuasiestáticos
El valor de slímite será de 0,2 para los gálibos GA, GB y GC.
4.5.3 CÁLCULO DEL GÁLIBO DE CARGAMENTO
4.5.3.1 Fórmulas de reducción para el gálibo GC
a) Reducción en secciones internas Eist
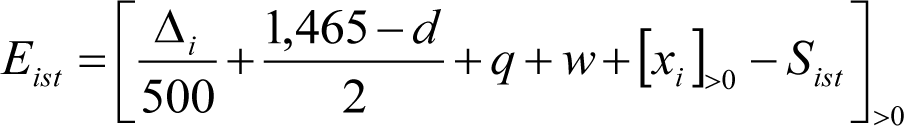
Como las holguras son constantes, las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=250 ó 150 m).
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||
|
|
||
| (1) valor a aplicar en E ist de partes bajas (h ≤ 0,430 m) | (2) valor a aplicar en E ist de partes altas (h > 0,430 m) | |
|
Si: |
||
|
|
||
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
||
| (1) valor a aplicar en E ist de partes bajas (h ≤ 0,430 m) | (2) valor a aplicar en E ist de partes altas (h > 0,430 m) | |
b) Reducción en secciones externas East
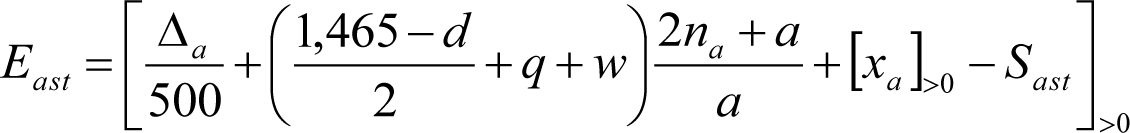
Análogamente, como las holguras son constantes, las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=250 ó 150 m).
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
|||
|
|
|||
| (1) valor a aplicar en E ast de partes bajas (h ≤ 0,430 m) | (2) valor a aplicar en E ast de partes altas (h > 0,430 m) | ||
|
Si: |
|||
|
|
|||
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
|||
| (1) valor a aplicar en E ast de partes bajas (h ≤ 0,430 m) | (2) valor a aplicar en E ast de partes altas (h > 0,430 m) | ||
4.5.3.2 Fórmulas de reducción para los gálibos GA y GB
Para h ≤ 3,22 m, los valores de Eist y East coinciden con los definidos en el apartado 4.5.3.1.
Para h > 3,22 m las fórmulas de reducción son las siguientes:
a) Reducción en secciones internas Eist
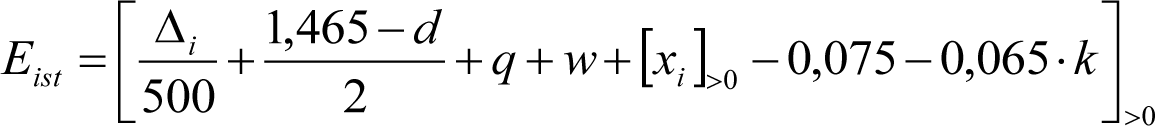
Si: 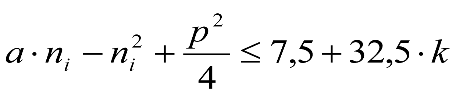 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
|
|
|
Si: |
|
|
|
siendo xi un factor para pasar de R=250 a 150 m, de valor:
|
b) Reducción en secciones externas East
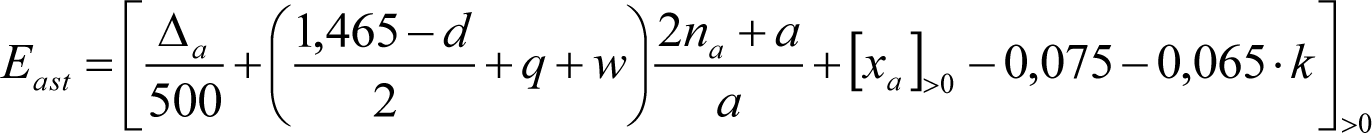
Si:  ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
|
|
|
|
|
Si: |
|
|
|
|
|
siendo xa un factor para pasar de R=250 a 150 m, de valor:
|
|
4.6 APLICACIÓN A LÍNEAS CON ANCHO MÉTRICO
4.6.1 CONTORNOS DE REFERENCIA
Se consideran los siguientes contornos de referencia:
∙ GEE10, para material que circule por líneas electrificadas.
∙ GED10, para material que circule por líneas no electrificadas.
Las dimensiones detalladas de cada contorno de referencia del Gálibo de Cargamento, a partir de una altura de 430 mm sobre carril, por secciones escalonadas cada 10 mm, se recogen en el anejo 8.
4.6.1.1 GEE10
4.6.1.1.1 Contorno de referencia de las partes altas
El contorno de referencia de las partes altas se define en la figura 4.9.
|
(1) Plano de rodadura NOTA: Partes bajas definidas en la figura 4.10 Figura 4.9. Contorno de referencia del gálibo estático GEE10. Partes altas |
4.6.1.1.2 Contorno de referencia de las partes bajas
La figura 4.10 define el contorno de referencia de las partes bajas.
|
(1) Plano de rodadura l: Ancho de vía Figura 4.10. Contorno de referencia del gálibo estático GEE10. Partes bajas |
4.6.1.2 GED10
El contorno de referencia de las partes altas se define en la figura 4.11.
El contorno de referencia de las partes bajas coincide con el definido en la figura 4.10 para el gálibo GEE10.
|
(1) Plano de rodadura NOTA: Partes bajas definidas en la figura 4.10 Figura 4.11. Contorno de referencia del gálibo estático GED10. Partes altas |
4.6.2 REGLAS ASOCIADAS
4.6.2.1 holguras laterales
De la expresión del apartado 4.2.2.2.1, se tiene:

siendo:
l: ancho de vía. Se toma: l= lmáx =lN+0,03=1,030m.
d = 0,970 m
El valor de q+w dependerá del tipo de material rodante, pudiendo tomarse como referencia un valor de 0,015 m.
4.6.2.2. Salientes
Se adoptarán los salientes indicados en el cuadro 4.5.
El saliente es igual al indicado en cuadro 2.18, excepto para h > 0,43m en que habría que añadir 0,045 m.
| Salientes máximos para un ancho de vía l y para una altura h del punto considerado sobre el plano de rodadura | |||
|---|---|---|---|
| Gálibo | Radio | h ≤ 0,43 m | h > 0,43m |
|
GEE10 GED10 |
100 ≤ R ≤ ∞ |
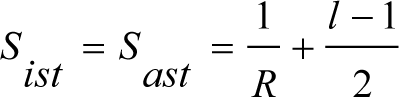
|

|
| 80 ≤ R < 100 |
|
|
|
|
NOTA: Sist = Lado interior de la curva (m); Sast = Lado exterior de la curva (m) |
|||
|
Cuadro 4.5. Salientes de los gálibos GEE10 y GED10 |
|||
4.6.2.3 Desplazamientos cuasiestáticos
El valor de slimite será de 0,3 para los gálibos GEE10 y GED10.
4.6.3 CÁLCULO DEL GÁLIBO DE CARGAMENTO
4.6.3.1 Fórmulas de reducción para los gálibos GEE10 y GED10
a) Reducción en secciones internas Eist

Como las holguras son constantes, las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=100 ó 80 m).
Si: 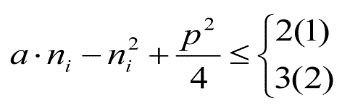 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
||
|
|
||
| (1) valor a aplicar en E ist de partes bajas (h ≤ 0,430 m) | (2) valor a aplicar en E ist de partes altas (h > 0,430 m) | |
|
Si: |
||
|
|
||
|
siendo xi un factor para pasar de R=100 a 80 m, de valor:
|
||
| (1) valor a aplicar en E ist de partes bajas (h ≤ 0,430 m) | (2) valor a aplicar en E ist de partes altas (h > 0,430 m) | |
b) Reducción en secciones externas East

Análogamente, como las holguras son constantes, las máximas reducciones se dan para el radio máximo (R=∞) o para el mínimo (R=100 ó 80 m).
Si: 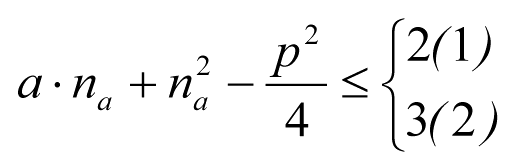 ⇒ La máx. reducción se da en recta (R=∞) ⇒ La máx. reducción se da en recta (R=∞) |
|
|
|
|
| (1) valor a aplicar en E ast de partes bajas (h ≤ 0,430 m) | (2) valor a aplicar en E ast de partes altas (h > 0,430 m) |
Si: 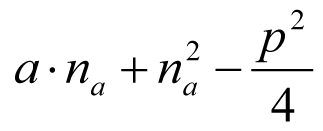 ⇒ La máx. reducción se da en curva (R=100 ó 80 m) ⇒ La máx. reducción se da en curva (R=100 ó 80 m) |
|
|
|
|
|
siendo xa un factor para pasar de R=100 a 80 m, de valor:
|
|
| (1) valor a aplicar en E ast de partes bajas (h ≤ 0,430 m) | (2) valor a aplicar en E ast de partes altas (h > 0,430 m) |
4.7 CUADROS DE REDUCCIÓN
4.7.1 CUADROS DE REDUCCIÓN DE LA ANCHURA DEL CARGAMENTO EN SECCIONES INTERNAS Y EXTERNAS
En el caso particular de cargamentos sobre vagones de dos ejes o de dos bogies, las reducciones del semiancho del contorno de referencia en secciones internas (Eist) y externas (East), para h > 0,43 m, se podrán calcular aplicando los cuadros de reducción incluidos en los anejos 9 y 10.
Se trata de cuadros de doble entrada, en las que a partir del empate, a, del vehículo y de la distancia, n, entre la sección transversal del vehículo considerada y el eje extremo más próximo (vagón de ejes) o el pivote más cercano (vagón de bogies), se obtiene la distancia mínima a respetar entre el cargamento y el contorno de referencia del gálibo de cargamento.
Estos cuadros se han obtenido aplicando las fórmulas de reducción de los apartados 4.4.3, 4.5.3 y 4.6.3, con los valores de holguras laterales totales y empate de bogie p siguientes:
a)En líneas con ancho de vía estándar europeo o ibérico:


Siendo:
d=1,410 m en líneas con ancho de vía estándar europeo
d=1,643 m en líneas con ancho de vía ibérico
p=0 en secciones externas y p=2 m en secciones internas (en el caso de vehículos con distintos valores de empate de bogies, se aplicará una corrección a los valores dados por los cuadros)
b)En líneas con ancho de vía métrico:
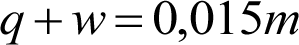
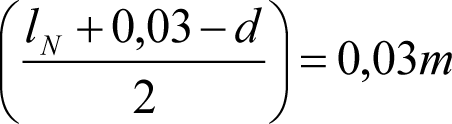
Siendo:
d=0,970 m
p=1,6 m en secciones externas y p=1,6 m en secciones internas (en el caso de vehículos con distintos valores de empate de bogies, se aplicará una corrección a los valores dados por los cuadros)
4.7.2 CUADROS DE REDUCCIÓN DE LA ANCHURA DEL CARGAMENTO RESPECTO DE LAS PAREDES LATERALES O TELEROS EN VAGONES DE SEGURIDAD E INTERMEDIOS
Para el caso de curvas de radio R=250m (anchos ibérico y estándar europeo) en el anejo 12 figura un cuadro con las distancias mínimas a respetar entre el cargamento y las paredes laterales o teleros de los vagones de seguridad e intermedios (utilizados para cargamentos que excedan la longitud útil del vagón).
Se trata de cuadros de doble entrada, en los que dichas distancias se obtienen a partir del empate, a, del vagón portador y de la distancia, n, entre la sección transversal considerada y el eje extremo más próximo (vagón de ejes) o el pivote más cercano (vagón de bogies) del vagón portador.
Ancho de vía (l): Distancia mínima entre las caras activas interiores de las cabezas de los carriles, medida a 14 mm por debajo del plano de rodadura.
Ancho estándar europeo: Es el que corresponde a un ancho de vía nominal de 1.435 mm.
Ancho ibérico: Es el que corresponde a un ancho de vía nominal de 1.668 mm.
Ancho métrico: Es el que corresponde a un ancho de vía nominal de 1.000 mm.
Andén: Acera paralela a las vías que se dispone en las estaciones para permitir a los viajeros la entrada y salida de los trenes.
Centro de balanceo (C): Para una sección transversal cualquiera de un vehículo, es el centro sobre el que rota la caja.
Coeficiente de adherencia (µ): Cociente entre la fuerza máxima de tracción en la llanta y la carga por eje, en el caso de vía sin peralte.
Coeficientes de desplazamiento (A): Son factores multiplicadores de las holguras laterales de los vehículos, que se aplican en el cálculo de las reducciones del semiancho del contorno de referencia.
Estos factores, son función de la posición de inscripción de los ejes de rodadura del vehículo sobre la vía, lo que a su vez depende de la tipología de éstos (ejes independientes, bogies motores, bogies portadores, etc.).
Coeficiente de flexibilidad (s): Sea una sección transversal cualquiera de un vehículo parado sobre una vía peraltada cuyo plano de rodadura forma un ángulo (δ) con la horizontal. Debido al descentramiento del peso y a la suspensión, la caja del vehículo girará respecto a su centro de balanceo (C), un ángulo (η). Se denomina coeficiente de flexibilidad (s) a la relación η/δ.
Contorno de referencia: Contorno llevado sobre los ejes de coordenadas, al objeto de definir el gálibo del material rodante, el gálibo de implantación de obstáculos o el gálibo de cargamento.
Contorno de referencia cinemático: Contorno llevado sobre los ejes de coordenadas, al objeto de definir el gálibo del material rodante y el gálibo de implantación de obstáculos mediante el método del gálibo cinemático.
Contorno de referencia estático: Contorno llevado sobre los ejes de coordenadas al objeto de definir el gálibo de cargamento mediante el método del gálibo estático.
Disimetría (η0): Para un vehículo parado sobre una vía horizontal, es el ángulo que formaría, en ausencia de rozamiento, el eje de la caja con la vertical. La causa de la disimetría puede ser una imperfección de construcción del vehículo, una desigualdad en el reglaje de las suspensiones o un descentramiento de la carga.
Ejes de coordenadas: Ejes ortogonales situados en un plano perpendicular al eje de la vía. El eje horizontal, es la intersección de dicho plano con el plano de rodadura. El eje vertical es perpendicular al plano de rodadura en el eje de la vía.
Empate: Distancia entre los centros de los ejes de rodadura de un vehículo.
Empate de un bogie: Distancia entre los centros de los ejes extremos del bogie.
Entreeje: Es la separación entre los ejes de dos vías contiguas. En el caso de vías con el mismo peralte, el entreeje será la distancia ortogonal entre las normales a los planos de rodadura que pasan por los ejes de ambas. En el caso de vías con diferente peralte, será la distancia medida paralelamente a la vía de menor peralte, entre la normal al plano de rodadura por el eje de la vía de menor peralte y la paralela que pasa por el eje de la vía de mayor peralte.
Entreeje límite: Distancia mínima entre los ejes de las vías adyacentes, para garantizar el paso del tráfico con total seguridad por las dos vías, respetando el gálibo elegido y evitando cualquier riesgo de interferencia entre los vehículos. Esta distancia es variable en función de los parámetros locales de la vía (peralte, radio de la curva, etc) y tiene en cuenta los márgenes de mantenimiento.
Entreeje nominal: Distancia entre los ejes de las vías adyacentes que tiene en cuenta generalmente un margen adecuado para permitir un diseño, montaje, vigilancia y mantenimiento cómodo, así como la circulación de transportes excepcionales o cualquier otro aspecto, como por ejemplo los efectos aerodinámicos.
Gálibo: Contorno de referencia, más unas reglas asociadas, que permiten definir el perfil constructivo máximo del material rodante, el perfil del cargamento y el perfil fuera del cual deben instalarse las estructuras fijas o provisionales.
Gálibo del material rodante: Contorno de referencia cinemático, más unas reglas que definen las reducciones a aplicar a dicho contorno. Estas reducciones son función de las características geométricas del material, de la posición de la sección en relación a los ejes, de la altura del punto considerado en relación al plano de rodadura, de las holguras de construcción, de los desgastes máximos previstos y de las características elásticas de la suspensión.
El contorno resultante de aplicar las reducciones define el espacio que no debe superar el perfil constructivo del material rodante.
Galibo de cargamento: Contorno de referencia estático más unas reglas que definen las reducciones a aplicar a dicho contorno. El contorno resultante define el espacio que no debe superar ni el cargamento, ni los teleros o paredes laterales de los vagones utilizados para la carga.
Gálibo de implantación de obstáculos: Espacio en torno a la vía, que no debe ser invadido por ningún objeto u obstáculo, ni por vehículos que circulen sobre vías adyacentes, al objeto de preservar la seguridad en la explotación.
Gálibo eléctrico del pantógrafo: Contorno de referencia más unas reglas asociadas, que permiten definir el espacio que debe respetarse teniendo en cuenta la distancia de aislamiento eléctrico, en relación a las partes en tensión del pantógrafo en posición de captación.
Gálibo límite de implantación de obstáculos: Espacio que no debe invadir ningún obstáculo en circunstancia alguna, a fin de permitir la circulación normal de los vehículos, más una reserva para considerar las variaciones tolerables de la posición de la vía que se producen entre dos operaciones normales de mantenimiento. Este gálibo se utiliza, por ejemplo, para comprobar si es posible el paso de transportes excepcionales por un determinado punto. Se define para un punto o tramo de línea.
Gálibo mecánico cinemático del pantógrafo: Contorno de referencia más unas reglas asociadas, que permiten definir el espacio fuera del cual deben instalarse las estructuras a fin de garantizar el paso del pantógrafo en posición de captación, teniendo en cuenta las tolerancias de mantenimiento y los desplazamientos considerados por la infraestructura.
Gálibo nominal de implantación de obstáculos: Espacio que no debe invadir ningún obstáculo en circunstancia alguna, a fin de permitir la circulación normal de los vehículos, más una reserva para considerar las variaciones tolerables de la posición de la vía que se producen entre dos operaciones normales de mantenimiento y unos márgenes complementarios para la circulación de transportes excepcionales, incrementos de velocidad, etc. Se define para un punto o tramo de línea.
Gálibo uniforme de implantación de obstáculos: Es un gálibo nominal obtenido para una envolvente de parámetros (radios, peraltes, etc.) suficientemente desfavorables, que no se superan en la mayor parte de la línea. De esta forma se puede utilizar un único gálibo para toda ella, comprobando que no se superan los parámetros de partida. Se define para una línea.
Índice de flexibilidad del pantógrafo: Es el desplazamiento lateral del frotador, a la altura máxima de verificación h’o, al someterle a una fuerza lateral de 300 N.
Perfil constructivo del material: Dimensiones exteriores de la sección transversal del material rodante considerado. Dicho perfil deberá estar inscrito en el gálibo del material rodante.
Plano de rodadura: Plano tangente a las cabezas de los dos carriles de una vía de ferrocarril, y que contiene al eje de ésta.
Punta matemática de la aguja (PMA): Intersección de las caras activas de la aguja y contraaguja. La punta real queda ligeramente retrasada por razones constructivas y funcionales.
Puntos PT: Punto lateral extremo de la línea superior horizontal del contorno de referencia.
Punto P: Punto extremo superior de los laterales externos del contorno de referencia.
Reglas asociadas: Reglas que, aplicadas a un contorno de referencia, permiten obtener el gálibo del material rodante, el gálibo de implantación de obstáculos y el gálibo de cargamento.
Saliente: Es lo que sobresaldría lateralmente, respecto al contorno de referencia, un vehículo de referencia (tipo) al inscribirse en curva y considerando sus holguras correspondientes.
Sección interna: Sección transversal del vehículo situada entre pivotes de bogies o entre ejes extremos de vehículos sin bogies.
Sección externa: Sección transversal del vehículo situada entre el extremo de éste y el pivote o eje extremo (en vehículos sin bogies) más próximo.
Tolerancias de construcción del vehículo: Desviaciones máximas admitidas entre las dimensiones exteriores reales y nominales del vehículo.
Tolerancia de construcción y fijación del pantógrafo: Desviación máxima admitida entre el eje de la caja del vehículo y el punto medio del frotador, situado a la altura máxima de verificación h’0 y en ausencia de solicitaciones laterales.
Tolerancia de reglaje de la suspensión: Para un vehículo vacío y en reposo sobre una vía horizontal, es el giro que experimenta una sección transversal de la caja, como consecuencia de imperfecciones en el reglaje de la suspensión. Este giro produce un desplazamiento adicional del pantógrafo de valor θ·(h-hc).
Vehículo de referencia: Vehículo teórico o real cuyos parámetros son utilizados para establecer las reglas asociadas a aplicar en la determinación del gálibo.
Vía: Conjunto de elementos que constituye el camino de rodadura del tren. Está compuesta por dos carriles cuya inclinación y separación relativa son mantenidas por las traviesas o por cualquier otro sistema equivalente.
Vía de circulación: Las utilizadas en la estación para la entrada, salida o paso de los trenes. Las otras vías de la estación, si dispone de ellas, se denominan vías de servicio.
Vía general: Vía principal o directa destinada al paso de los trenes directos sin parada en la estación.
Vía sobre balasto: Sistema tradicional de vía constituido por carriles, traviesas y balasto, que transmite las cargas ferroviarias que recibe de los carriles a través de las traviesas.
Vía en placa: Sistema de vía en el que los carriles asientan directa o indirectamente sobre una losa continua, con interposición de elastómeros o dispositivos semejantes.
| Parámetro | Definición | Unidad |
|---|---|---|
| a | Empate. Distancia entre pivotes de bogies o entre ejes extremos de vehículos sin bogies. | m |
| a nccaja | Aceleración centrífuga no compensada a nivel de caja. | m/s 2 |
| a ncvía | Aceleración centrífuga no compensada a nivel de vía. | m/s 2 |
| A i | Coeficiente que depende del vehículo de referencia, para el cálculo de los salientes en el interior de la curva | |
| A a | Coeficiente que depende del vehículo de referencia, para el cálculo de los salientes en el exterior de la curva | |
| A p | Coeficiente de desplazamiento correspondiente al término (p 2/4), en el caso de vehículos con bogies. | |
| A q | Coeficiente de desplazamiento correspondiente a la holgura lateral entre eje de ruedas y bastidor del bogie, o entre eje y caja, en vehículos sin bogies. | |
| A w | Coeficiente de desplazamiento correspondiente a la holgura lateral entre bastidor del bogie y caja. | |
| A wv | Coeficiente de desplazamiento correspondiente a la holgura lateral entre eje de ruedas y vía. | |
| Aff | Descenso de las suspensiones. | m |
| b | Distancia desde cualquier punto del contorno del vehículo a su eje de simetría, medida en una sección transversal, paralelamente al plano de rodadura. Corresponde al semiancho del vehículo en ese punto. | m |
| b andén,a | Distancia entre la vertical del eje de la vía y el borde del andén, medida en una sección transversal, paralelamente al plano horizontal y hacia el exterior de la curva. | m |
| b andén,a,lím | Distancia límite entre la vertical del eje de la vía y el borde del andén, medida en una sección transversal, paralelamente al plano horizontal y hacia el exterior de la curva. | m |
| b andén,i | Distancia entre la vertical del eje de la vía y el borde del andén, medida en una sección transversal, paralelamente al plano horizontal y hacia el interior de la curva. | m |
| b andén,i,lím | Distancia límite entre la vertical del eje de la vía y el borde del andén, medida en una sección transversal, paralelamente al plano horizontal y hacia el interior de la curva. | m |
| b carg | Semiancho máximo del cargamento a una altura h sobre el plano de rodadura. | m |
| b CR | Semiancho del contorno de referencia cinemático. Distancia desde cualquier punto del contorno de referencia cinemático a su eje de simetría, medida paralelamente al plano de rodadura. | m |
| b CRst | Semiancho del contorno de referencia estático. Distancia desde cualquier punto del contorno de referencia estático a su eje de simetría, medida paralelamente al plano de rodadura. | m |
| b elec | Distancia de aislamiento eléctrico, medida en una sección transversal, paralelamente al plano de rodadura. | m |
| b G | Semidistancia entre ejes de resbaladera, medida en una sección transversal, paralelamente al plano de rodadura. | m |
| b obstáculo,a | Distancia entre la perpendicular al plano de rodadura en el eje de la vía y el obstáculo, medida en una sección transversal, paralelamente al plano de rodadura y hacia el exterior de la curva. | m |
| b obstáculo,a,elec | Valor de b obstáculo,a, en el caso de obstáculos situados en la parte del pantógrafo sometido a tensión eléctrica. | m |
| b obstáculo,i | Distancia entre la perpendicular al plano de rodadura en el eje de la vía y el obstáculo, medida en una sección transversal, paralelamente al plano de rodadura y hacia el interior de la curva. | m |
| b obstáculo,i,elec | Valor de b obstáculo,i, en el caso de obstáculos situados en la parte del pantógrafo sometido a tensión eléctrica. | m |
| b qa | Distancia entre la perpendicular al plano de rodadura en el eje de la vía y el borde del andén, medida en una sección transversal, paralelamente al plano de rodadura y hacia el exterior de la curva. | m |
| b qa,lím | Distancia límite entre la perpendicular al plano de rodadura en el eje de la vía y el borde del andén, medida en una sección transversal, paralelamente al plano de rodadura y hacia el exterior de la curva. | m |
| b qi | Distancia entre la perpendicular al plano de rodadura en el eje de la vía y el borde del andén, medida en una sección transversal, paralelamente al plano de rodadura y hacia el interior de la curva. | m |
| b qi,lím | Distancia límite entre la perpendicular al plano de rodadura en el eje de la vía y el borde del andén, medida en una sección transversal, paralelamente al plano de rodadura y hacia el interior de la curva. | m |
| b qo |
Máxima distancia entre el umbral del peldaño y el eje de la vía, medida en una sección transversal, paralelamente al plano de rodadura. |
m |
| b PT | Distancia desde los puntos PT al eje de simetría del contorno de referencia cinemático, medida paralelamente al plano de rodadura. | m |
| b veh | Semiancho máximo del vehículo a una altura h sobre el plano de rodadura. | m |
| b w | Semiancho de la mesilla del pantógrafo. | m |
| b 2 | Semidistancia entre los muelles de la suspensión secundaria, medida en una sección transversal, paralelamente al plano de rodadura. | m |
| B i | Coeficiente que depende del vehículo de referencia, para el cálculo de los salientes en el interior de la curva | |
| B a | Coeficiente que depende del vehículo de referencia, para el cálculo de los salientes en el exterior de la curva | |
| c w | Ancho del trocador aislado proyectado perpendicularmente sobre el plano de rodadura. | m |
| C | Centro de balanceo (rotación) de la caja del vehículo debido al efecto del peralte y las disimetrías. | |
| d | Distancia mínima entre las caras activas de las pestañas de las ruedas de un eje, medida a 10 mm por debajo del círculo de rodadura, con ambas pestañas al límite de desgaste. | m |
| d’’ | Distancia entre caras internas de carril a la altura del piquete de vía. | m |
| dg | Desplazamiento geométrico por inscripción en curva. Corresponde al desplazamiento lateral del eje de simetría de una sección transversal del vehículo, respecto a la perpendicular al plano de rodadura por el eje de la vía. | m |
| dg a | Valor de dg, para secciones externas. | m |
| dg i | Valor de dg, para secciones internas. | m |
| dg v | Desplazamiento geométrico por inscripción en acuerdos verticales. Corresponde al desplazamiento de una sección transversal del vehículo perpendicularmente al plano de rodadura. | |
| dg av | Valor de dg v, para secciones externas. | m |
| dg iv | Valor de dg v, para secciones internas. | m |
| D | Peralte de la vía. | m |
| D’ | Peralte de vía intermedio entre 0 y D máx, en el caso de vehículos de caja inclinable. | m |
| D máx | Peralte máximo considerado en la determinación del gálibo del material rodante. | m |
| D o | Peralte adoptado por convenio entre el material rodante y la infraestructura. | m |
| D’ o | Peralte adoptado por convenio entre el material rodante y la infraestructura, considerado en la determinación del gálibo del pantógrafo. | m |
| Dpl cin | Desplazamiento cinemático lateral del vehículo, medido en una sección transversal, paralelamente al plano de rodadura. | m |
| Dpl acin | Desplazamiento cinemático lateral del vehículo en secciones externas, medido en una sección transversal, paralelamente al plano de rodadura. | m |
| Dpl icin | Desplazamiento cinemático lateral del vehículo en secciones internas, medido en una sección transversal, paralelamente al plano de rodadura. |
m |
| Dpl st | Desplazamiento estático lateral del cargamento, medido en una sección transversal, paralelamente al plano de rodadura. | m |
| Dpl ast | Desplazamiento estático lateral del cargamentoo en secciones externas, medido en una sección transversal, paralelamente al plano de rodadura. | m |
| Dpl ist | Desplazamiento estático lateral del cargamento en secciones internas, medido en una sección transversal, paralelamente al plano de rodadura. | m |
| D th | Peralte de equilibrio. Corresponde a una aceleración centrífuga no compensada en el vehículo nula. | m |
| e a | Reducción del contorno de referencia perpendicularmente al plano de rodadura, en las partes bajas y altas de los vehículos, en secciones externas. Se traduce en incrementos de la altura mínima y en reducciones de la altura máxima. | m |
| e i | Reducción del contorno de referencia perpendicularmente al plano de rodadura, en las partes bajas y altas de los vehículos, en secciones internas. Se traduce en incrementos de la altura mínima y en reducciones de la altura máxima. | m |
| e i1 | Elevación normal de la altura mínima del contorno de referencia perpendicular al plano de rodadura, en secciones internas, en el caso de vehículos con a≤17,80 m, a fin de permitir el paso por los frenos de vía. | m |
| e i2 | Elevación reducida de la altura mínima del contorno de referencia perpendicular al plano de rodadura, en secciones internas, en el caso de vehículos con a≤15,80 m, a fin de permitir el paso por los frenos de vía. | m |
| e’ i1 | ei1 en el caso de vehículos con a>17,80 m. | m |
| e’ i2 | ei2 en el caso de vehículos con a>15,80 m. | m |
| e p | Máximo desplazamiento lateral del pantógrafo, respecto al eje de simetría del vehículo, con su eje de ruedas centrado respecto al eje de vía. Se utiliza en la determinación del gálibo mecánico del pantógrafo. | m |
| e po | Valor de e p para la altura máxima (h’ o) de verificación del gálibo del pantógrafo. | m |
| e pu | Valor de e p para la altura mínima (h’ u) de verificación del gálibo del pantógrafo. | m |
| e* p | Máximo desplazamiento lateral del pantógrafo en el caso de un vehículo tipo, respecto al eje de simetría del vehículo, que no deberá ser rebasado por los desplazamientos laterales máximos del pantógrafo en el vehículo real. | m |
| e * po | Valor de e* p para la altura máxima (h’ o) de verificación del gálibo del pantógrafo. | m |
| e * pu | Valor de e* p para la altura mínima (h’ u) de verificación del gálibo del pantógrafo. | m |
| e v | Reducción de la altura del freno de vía en posición activa en relación a las cotas 0,115/0,125 o 0,08 m, en el tramo comprendido entre x = 0 y x = 3 o 5m del final del acuerdo vertical convexo. | m |
| e v1 | Valor de e v en el caso de lomos de asno clásicos, con x = 3 m. | m |
| e v2 | Valor de e v en el caso de lomos de asno donde operen vagones, como los de transporte combinado, con x = 5 m. | m |
| E a | Reducción de la semianchura del contorno de referencia, en secciones externas, medido en una sección transversal, paralelamente al plano de rodadura. | m |
| E i | Reducción de la semianchura del contorno de referencia, en secciones internas, medido en una sección transversal, paralelamente al plano de rodadura. | m |
| E 0a | Valor de E a a la altura máxima (h’ o) de verificación del gálibo del pantógrafo. | m |
| E 0i | Valor de E i a la altura máxima (h’ o) de verificación del gálibo del pantógrafo. | m |
| E ua | Valor de E a a la altura mínima (h’ u) de verificación del gálibo del pantógrafo. | m |
| E ui | Valor de E i para la altura mínima (h’ u) de verificación del gálibo del pantógrafo. | m |
| E* 0i | Valor de E 0i para el caso de vehículo real dotado de pantógrafo dependiente del sistema de inclinación de la caja. | m |
| E* 0a | Valor de E 0a para el caso de vehículo real dotado de pantógrafo dependiente del sistema de inclinación de la caja. | m |
| E* ui | Valor de E ui para el caso de vehículo real dotado de pantógrafo dependiente del sistema de inclinación de la caja. | m |
| E* ua | Valor de E ua para el caso de vehículo real dotado de pantógrafo dependiente del sistema de inclinación de la caja. | m |
| E tipo,a | Valor de E a para el caso de vehículo tipo. | m |
| E tipo,i | Valor de E i para el caso de vehículo tipo. | m |
| E tipo,oa | Valor de E tipo,a para la altura máxima (h’ o) de verificación del gálibo del pantógrafo. | m |
| E tipo,oi | Valor de E tipo,i para la altura máxima (h’ o) de verificación del gálibo del pantógrafo. | m |
| E tipo,ua | Valor de E tipo,a para la altura mínima (h’ u) de verificación del gálibo del pantógrafo. | m |
| E tipo,ui | Valor de E tipo,i para la altura mínima (h’ u) de verificación del gálibo del pantógrafo. | m |
| EA | Distancia entre ejes de vías (entreeje). | m |
| f s | Elevación del hilo de contacto debido a la fuerza ascendente transmitida por el pantógrafo, medida perpendicularmente al plano de rodadura. | m |
| f wa | Elevación del arco del pantógrafo por encima del plano de contacto debido al desgaste de la pletina o frotador, medida perpendicularmente al plano de rodadura. | m |
| f ws | Elevación del arco del pantógrafo por encima del plano de contacto debido a la flexibilidad del pantógrafo, medida perpendicularmente al plano de rodadura. | m |
| F est | Fuerza de contacto estática entre el pantógrafo y la catenaria, actuando perpendicularmente al plano de rodadura. | N |
| F lc | Descenso de la caja del vehículo debido a deformaciones de su estructura, medido perpendicularmente al plano de rodadura. | m |
| F m | Fuerza de contacto media entre el pantógrafo y la catenaria, actuando perpendicularmente al plano de rodadura. | N |
| F max | Fuerza de contacto máxima entre el pantógrafo y la catenaria, actuando perpendicularmente al plano de rodadura. |
N |
| F w | Fuerza máxima de tracción en el contacto entre las llantas del eje del vehículo y el carril. | kN |
| g | Aceleración de la gravedad. | m/s 2 |
| g’ | Diferencia entre el gálibo considerado en la vía directa de un aparato de vía y el semiancho de vía nominal. | m |
| g’’ | Diferencia entre el gálibo considerado en la vía desviada de un aparato de vía y el semiancho de vía nominal. | m |
| G | Centro de gravedad del vehículo. | |
| h | Altura de un punto del contorno del vehículo, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h c | Altura del centro de balanceo del vehículo, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h o | Altura del centro de rotación de la caja del vehículo, en el caso de vehículos de caja inclinable, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h p | Altura del centro de rotación del pantógrafo, en el caso de pantógrafos dependientes del sistema de inclinación de la caja, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h PT | Altura de los puntos PT, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h co | Valor de h c adoptado por convenio entre el material rodante y la infraestructura. | m |
| h’ co | Altura del centro de balanceo del vehículo utilizada en el cálculo del gálibo del pantógrafo, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h ccaja | Altura del centro de balanceo (rotación) de la suspensión secundaria, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h cvía | Altura del centro de balanceo (rotación) de la suspensión primaria, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h CR | Altura de un punto del contorno de referencia, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h eff | Altura del gálibo mecánico del pantógrafo. Altura efectiva del pantógrafo elevado, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h eff,elec | Altura del gálibo eléctrico del pantógrafo. Altura efectiva del pantógrafo elevado incluyendo la distancia de aislamiento eléctrico, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h f | Altura del hilo de contacto, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
|
h i |
Altura del tope inferior de basculación de la caja, en los VCIs tipo TALGO, medida sobre el plano de rodadura y perpendicularmente a éste. |
m |
|
h minCR |
Altura de la esquina inferior del contorno de referencia. |
m |
|
h nez |
Altura del bordillo del borde de andén. |
m |
| h min | Altura inferior del contorno de referencia a considerar en la determinación de las características del vehículo de referencia. | m |
| h max | Altura superior del contorno de referencia a considerar en la determinación de las características del vehículo de referencia. | m |
| h s | Altura del tope superior de basculación de la caja, en los VCIs tipo TALGO, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h umín | Altura mínima considerada para el desplazamiento vertical por inscripción en acuerdos verticales del material rodante por debajo del contorno de referencia | m |
| h obstáculo,i | Altura máxima (bajo el contorno de referencia) o mínima (sobre el contorno de referencia) a la que deben situarse los obstáculos, medida sobre el plano de rodadura y perpendicularmente a éste, en el lado interior de la curva. | m |
| h obstáculo,a | Altura máxima (en zona inferior del contorno de referencia) o mínima (en zona superior del contorno de referencia) a la que deben situarse los obstáculos, medida sobre el plano de rodadura y perpendicularmente a éste, en el lado exterior de la curva. | m |
| h q | Altura del borde de andén, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h t | Altura de la articulación más baja del pantógrafo, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h omín | Altura mínima considerada para el desplazamiento vertical por inscripción en acuerdos verticales del material rodante por encima del contorno de referencia | m |
| h’ o | Altura máxima de verificación del gálibo del pantógrafo en posición de captación, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| h’ u | Altura mínima de verificación del gálibo del pantógrafo en posición de captación, medida sobre el plano de rodadura y perpendicularmente a éste. | m |
| I | Insuficiencia de peralte. | m |
| I c | Insuficiencia de peralte máxima admitida por el Administrador de la infraestructura ferroviaria, en el caso de vehículos de caja inclinable. | m |
| I máx | Insuficiencia de peralte máxima considerada en la determinación del gálibo del material rodante. | m |
| I o | Insuficiencia de peralte adoptada por convenio entre el material rodante y la infraestructura. | m |
| I p | Insuficiencia de peralte máxima a considerar en los vehículos de caja inclinable. | m |
| I’ c | Insuficiencia de peralte intermedia entre 0 y I c, en el caso de vehículos de caja inclinable. | m |
| I’ p | Insuficiencia de peralte intermedia entre 0 e I p, en el caso de vehículos de caja inclinable. | m |
| I’ o | Insuficiencia de peralte adoptada por convenio entre el material móvil y la infraestructura, considerada en la determinación del gálibo del pantógrafo. | m |
| j’ a | Desplazamiento lateral adicional del pantógrafo del vehículo real, respecto al vehículo tipo, debido a holguras laterales, en secciones externas. | m |
| j’ i | Desplazamiento lateral adicional del pantógrafo del vehículo real, respecto al vehículo tipo, debido a holguras laterales, en secciones internas. | m |
| J | Juego (holgura) de las resbaladeras. | m |
| k | Factor de proporcionalidad que permite obtener el saliente a diferentes alturas. | |
| K | Factor de seguridad a aplicar a los desplazamientos aleatorios horizontales y verticales, en la determinación del gálibo límite de implantación de obstáculos. | |
| K' | Factor de seguridad a aplicar a los desplazamientos aleatorios horizontales y verticales, en la determinación del gálibo mecánico del pantógrafo. | |
| l | Ancho de vía. | m |
| l máx | Ancho de vía máximo teórico. | m |
| l N | Ancho de vía nominal. | m |
| L | Distancia entre los círculos de rodadura de las ruedas de un eje. | m |
| L i | Distancia entre la vertical del lado interior del carril y el borde del andén, medida en una sección transversal, paralelamente al plano horizontal y hacia el interior de la curva. | m |
| L e | Distancia entre la vertical del lado interior del carril y el borde del andén, medida en una sección transversal, paralelamente al plano horizontal y hacia el exterior de la curva. | m |
| M e | Carga por eje del vehículo. | kN |
| M EA1 +M EA2 | Desplazamientos aleatorios laterales considerados en la determinación de los entreejes límite y nominal. | m |
| M EA3 | Margen complementario lateral considerado en la determinación del entreeje nominal. | m |
| M 1 +M 2 | Desplazamientos aleatorios laterales considerados en la determinación de los gálibos límite y nominal de implantación de obstáculos. | m |
| M 3b | Margen complementario lateral considerado en la determinación del gálibo nominal de implantación de obstáculos. | m |
| M 3h | Margen complementario perpendicular al plano de rodadura considerado en la determinación del gálibo nominal de implantación de obstáculos. | m |
| n | Distancia entre cualquier sección transversal de un vehículo y el pivote de bogie o eje extremo (en vehículos sin bogies) más próximo. | m |
| n a | Distancia entre cualquier sección transversal externa de un vehículo y el pivote de bogie o eje extremo (en vehículos sin bogies) más próximo. | m |
| n i | Distancia entre cualquier sección transversal interna de un vehículo y el pivote de bogie o eje extremo (en vehículos sin bogies) más próximo. | m |
| n μ | Distancia entre cualquier sección transversal interna de un vehículo y el pivote del bogie motor, en un vehículo con un bogie motor y otro portador. | m |
| p | Empate del bogie. Es la distancia entre sus ejes extremos | m |
| p’ | Empate del bogie portador, en vehículos con un bogie motor y otro portador. | m |
| P a | Diferencia entre los desplazamientos laterales del pantógrafo en el vehículo real y el vehículo tipo, en secciones externas. | m |
| P i | Diferencia entre los desplazamientos laterales del pantógrafo en el vehículo real y el vehículo tipo, en secciones internas. | m |
| P oa | Diferencia entre los desplazamientos laterales del pantógrafo en el vehículo real y el vehículo tipo, para una altura de h’ 0, medido en una sección transversal, paralelamente al plano de rodadura, en secciones externas. | m |
| P oi | Diferencia entre los desplazamientos laterales del pantógrafo en el vehículo real y el vehículo tipo, para una altura de h’ 0, medido en una sección transversal, paralelamente al plano de rodadura, en secciones internas. | m |
| P ua | Diferencia entre los desplazamientos laterales del pantógrafo en el vehículo real y el vehículo tipo, para una altura de h’ u, medido en una sección transversal, paralelamente al plano de rodadura, en secciones externas. | m |
| P ui | Diferencia entre los desplazamientos laterales del pantógrafo en el vehículo real y el vehículo tipo, para una altura de h’ u, medido en una sección transversal, paralelamente al plano de rodadura, en secciones internas. | m |
| P | Punto extremo superior de los laterales externos del contorno de referencia. | |
| PT | Punto lateral extremo de la línea superior horizontal del contorno de referencia. | |
| PMA | Punta matemática de la aguja. | |
| PMC | Punta matemática del corazón del desvío. | |
| q | Holgura lateral entre eje de ruedas y bastidor de bogie o entre eje de ruedas y caja, en vehículos sin bogie. | m |
| qs | Desplazamiento cuasiestático lateral considerado en la determinación del gálibo de implantación de obstáculos. | m |
| qs a | Valor de qs, en el exterior de la curva. | m |
| qs i | Valor de qs, en el interior de la curva. | m |
| qs’ | Desplazamiento cuasiestático lateral considerado en la determinación del gálibo mecánico del pantógrafo. | m |
| qs’ a | Valor de qs’, en el exterior de la curva. | m |
| qs’ i | Valor de qs’, en el interior de la curva. | m |
| R | Radio de curva en planta. | m |
| R v | Radio de curvatura de acuerdo vertical. | m |
| R vmín | Radio de curvatura mínimo de acuerdo vertical. | m |
| s | Coeficiente de flexibilidad del vehículo. | |
| s 0 | Coeficiente de flexibilidad del vehículo adoptado por convenio entre el material rodante y la infraestructura. | |
| s 1 | Coeficiente de flexibilidad de la suspensión primaria del vehículo. | |
| s 2 | Coeficiente de flexibilidad de la suspensión secundaria del vehículo. | |
| s n | Coeficiente de flexibilidad de la estructura portante del pantógrafo en el caso de pantógrafos independientes del sistema de inclinación de la caja del vehículo. | |
| s’ 0 | Coeficiente de flexibilidad del vehículo, considerado en la determinación del gálibo del pantógrafo. | |
| s limite | Coeficiente de flexibilidad admisible del vagón+cargamento, para la aplicación del método estático en el cálculo del gálibo de cargamento. | |
| S | Saliente cinemático. Es lo que sobresaldría lateralmente, respecto al contorno de referencia cinemático, un vehículo de referencia (tipo) al inscribirse en curva, considerando sus holguras correspondientes. | m |
| S a | Saliente cinemático hacia el lado exterior de la curva. | m |
| S i | Saliente cinemático hacia el lado interior de la curva. | m |
| S l | Parte del saliente correspondiente a la mitad de la diferencia entre el ancho de vía real y el nominal. | m |
| S R | Diferencia entre el saliente total y S l. Esta parte del saliente depende del radio de curvatura R. | m |
| S st | Saliente estático. Es lo que sobresaldría lateralmente, respecto al contorno de referencia estático, un vehículo de referencia (tipo) al inscribirse en curva, considerando sus holguras correspondientes. | m |
| S ast | Saliente estático hacia el exterior de la curva | m |
| S ist | Saliente estático hacia el interior de la curva | m |
| S’ a | Saliente hacia el lado exterior de la curva en el cálculo del pantógrafo. | m |
| S’ i | Saliente hacia el lado interior de la curva en el cálculo del pantógrafo. | m |
| t | Índice de flexibilidad del pantógrafo, utilizado en el cálculo de z’ y z». | m |
| T D | Diferencia de peralte de la vía entre dos operaciones sucesivas de mantenimiento periódico. | m |
| T N |
Desplazamiento vertical de la vía entre dos operaciones sucesivas de mantenimiento periódico. Corresponde a un desplazamiento idéntico de ambos carriles perpendicularmente al plano de rodadura, por encima o por debajo de su nivel teórico. Para las partes bajas entre carriles y para aquellos obstáculos que se muevan solidariamente con la vía el desplazamiento vertical será el correspondiente al desgaste de los carriles. |
m |
| T q | Tolerancias para construcción y mantenimiento de andenes. | m |
| T vía | Desplazamiento lateral de la vía entre dos operaciones sucesivas de mantenimiento periódico. | m |
| U sr | Desgaste máximo de las llantas de un vehículo. Diferencia entre su radio nominal y el radio mínimo admisible tras realizar operaciones de reperfilado. | m |
| v | Velocidad del vehículo. | m/s |
| V | Velocidad del vehículo. | km/h |
| V c | Velocidad máxima de los vehículos clásicos. | km/h |
| V máx | Velocidad máxima admisible por la infraestructura en un determinado punto o tramo de la línea. | km/h |
| V p | Velocidad máxima de los vehículos de caja inclinable. | km/h |
| w | Holgura lateral entre bastidor de bogie y caja. | m |
| w a(R) | Valor de w en el lado exterior de una curva de radio R. | m |
| w i(R) | Valor de w en el lado interior de una curva de radio R. | m |
| w ∞ | Valor de w en alineación recta. | m |
| w v | Holgura lateral entre eje de ruedas y vía. | m |
| w’ a(R) | Valor de w en el lado exterior de una curva de radio R, para el bogie portador de un vehículo con un bogie motor y otro portador. | m |
| w’ i(R) | Valor de w en el lado interior de una curva de radio R, para el bogie portador de un vehículo con un bogie motor y otro portador. | m |
| w’ ∞ | Valor de w en alineación recta, para el bogie portador de un vehículo con un bogie motor y otro portador. | m |
| w * | Holgura lateral entre la estructura soporte de los elementos de rodadura y la caja del vehículo, en los vehículos tipo TALGO, con ruedas independientes. | m |
| w * a(R) | Valor de w * en el lado exterior de una curva de radio R. | m |
| w * i(R) | Valor de w * en el lado interior de una curva de radio R. | m |
| w * ∞ | Valor de w * en alineación recta. | m |
| W I | Holgura entre la caja y la estructura del vehículo en el tope lateral inferior. | m |
| W I,a(R) | Holgura entre la caja y la estructura del vehículo en el tope lateral inferior, en el lado exterior de una curva de radio R. | m |
| W I,i(R) | Holgura entre la caja y la estructura del vehículo en el tope lateral inferior, en el lado interior de una curva de radio R. | m |
| W I∞ | Holgura entre la caja y la estructura del vehículo en el tope lateral inferior, en alineación recta. | m |
| W S | Holgura entre la caja y la estructura del vehículo en el tope lateral superior. | m |
| W S,a(R) | Holgura entre la caja y la estructura del vehículo en el tope lateral superior, en el lado exterior de una curva de radio R. | m |
| W S,i(R) | Holgura entre la caja y la estructura del vehículo en el tope lateral superior, en el lado interior de una curva de radio R. | m |
| W S∞ | Holgura entre la caja y la estructura del vehículo en el tope lateral superior, en alineación recta. | m |
| x | Distancia entre una sección de vía y el inicio de un acuerdo vertical próximo. Se emplea en el cálculo de e a, e i y e v. | m |
| x a | Sumando a añadir a E a para transformar su valor correspondiente a un radio R=250m, en el valor correspondiente a R=150m (en líneas con ancho ibérico y estándar europeo). En líneas de ancho métrico la transformación es de radio R=100m a R=80m. | m |
| x i | Sumando a añadir a E i para transformar su valor correspondiente a un radio R=250m, en el valor correspondiente a R=150m (en líneas con ancho ibérico y estándar europeo). En líneas de ancho métrico la transformación es de radio R=100m a R=80m. | m |
| y | Distancia entre el pivote ficticio y el centro geométrico del bogie, en bogies sin pivote. | m |
| z | Desplazamientos cuasiestáticos totales a considerar en la determinación del gálibo del material rodante. Es la suma de z 1+z 2. | m |
| z p | Valor de z considerado en la determinación del gálibo de los vehículos de caja inclinable. | m |
| z total | Desplazamiento cuasiestático total producido por los vehículos de caja inclinable. Una parte se considera en la determinación del gálibo del material rodante y otra parte en el de implantación de obstáculos. | m |
| z 0 | Desplazamiento cuasiestático fijo a considerar en el cálculo del gálibo de cargamento. | m |
| z 1 | Desplazamiento cuasiestático debido a un exceso o insuficiencia de peralte y a la flexibilidad de la suspensión del vehículo. Se aplica en la determinación del gálibo del material rodante. | m |
| z 1p | Valor de z 1 considerado en la determinación del gálibo del pantógrafo en los vehículos de caja inclinable. | m |
| z 2 | Desplazamiento cuasiestático debido a una disimetría del vehículo mayor de 1.º, debida a eventuales tolerancias de construcción ó reglaje de la suspensión del vehículo, o a un reparto asimétrico de sus cargas. Se aplica en la determinación del gálibo del material rodante. | m |
| z’ | Desplazamiento lateral adicional del pantógrafo del vehículo real, respecto el vehículo tipo, debido a los siguientes factores: 1) exceso o insuficiencia de peralte I’ 0 ó D’ 0; 2) flexibilidad y tolerancia de construcción y fijación del pantógrafo, y 3) tolerancia de reglaje de la suspensión para una altura de h’ 0. | m |
| z’ p | Valor de z’ en el caso de vehículos de caja inclinable. | m |
| z’’ | Desplazamiento lateral adicional del pantógrafo del vehículo real, respecto el vehículo tipo, debido a los siguientes factores: 1) exceso o insuficiencia de peralte I’ 0 ó D’ 0; 2) flexibilidad y tolerancia de construcción y fijación del pantógrafo, y 3) tolerancia de reglaje de la suspensión para una altura de h’ u. | m |
| z’’ p | Valor de z’’ en el caso de vehículos de caja inclinable | m |
| z* |
Desplazamiento que tiene en cuenta la inclinación de la caja del vehículo impuesta por el sistema activo, en los vehículos de caja inclinable.
|
m |
| α | Ángulo de contrarrotación del pantógrafo. | (º) |
| α * | Inclinación suplementaria de la caja debido al juego (holgura) de las resbaladeras. | (º) |
| α’ | Ángulo de la parte inclinada del arco del pantógrafo respecto un plano horizontal. | (º) |
| α’’ | Ángulo del desvío. | (º) |
| α c | Giro del vehículo alrededor de su centro de balanceo, debido a una asimetría transversal de la carga. | (º) |
| α PT,D | Máxima rotación cuasiestática del vehículo hacia el interior de la curva. | (º) |
| α PT,I | Máxima rotación cuasiestática del vehículo hacia el exterior de la curva. | (º) |
| α osc | Giro del vehículo alrededor de su centro de balanceo, debido a oscilaciones aleatorias causadas por irregularidades de la vía. | (º) |
| α susp | Giro del vehículo alrededor de su centro de balanceo, debido a una disimetría causada por las tolerancias en el reglaje de la suspensión. | (º) |
| β | Giro de la caja del vehículo impuesto por el sistema de inclinación activo. | rad |
| β * | Reducción aplicada en el cálculo de e *po, con el fin de cubrir el carácter aleatorio de los desplazamientos laterales del pantógrafo. | m |
| β | Ángulo de la aguja. | rad |
| β’’ | Angulo que define la posición del piquete de vía respecto la vía desviada de un aparato de vía. | (º) |
| γ c | Aceleración centrífuga de un vehículo en curva. | m/s 2 |
| γ c ’ | Aceleración centrífuga no compensada de un vehículo en curva con peralte inferior al de equilibrio. | m/s 2 |
|
δ |
Inclinación transversal de la vía peraltada. Ángulo que forma el plano de rodadura con el horizontal en una sección de vía peraltada. |
(º) |
|
δq,a |
Separación horizontal del andén en el lado exterior de la curva respecto el gálibo límite de implantación de obstáculos inclinado un ángulo δ. |
m |
| δ h | Distancia que determina la zona a la que puede ubicarse el umbral del peldaño respecto b qo. | m |
| δ v+ | Máxima elevación del peldaño sobre el andén. | m |
| δ v- | Máxima depresión del peldaño bajo el andén. | m |
| δ * | Reducción aplicada en el cálculo de e *pu, con el fin de cubrir el carácter aleatorio de los desplazamientos laterales del pantógrafo. | m |
| Δ | Saliente debido al ángulo del desvío. | m |
| ΔAff | Diferencia de descenso de las suspensiones, en sentido longitudinal o transversal. | m |
| Δb c | Desplazamiento cuasiestático paralelo al plano de rodadura debido a desviaciones del peralte (T D). | m |
| Δb g | Desplazamiento geométrico paralelo al plano de rodadura debido a desviaciones del peralte (T D). | m |
| Δb osc | Desplazamiento paralelo al plano de rodadura debido a oscilaciones del vehículo causadas por irregularidades de la vía. | m |
| Δb δD | Acercamiento entre las partes altas de dos vehículos situados en vías contiguas, debido a la diferencia de peraltes de ambas. Se utiliza en la determinación de la distancia entre ejes de vías. | m |
| Δb ηo | Desplazamiento paralelo al plano de rodadura debido a disimetrías del vehículo. | m |
| Δh PT | Desplazamiento cuasiestático perpendicular al plano de rodadura a considerar en la determinación del gálibo de implantación de obstáculos. | m |
| Δh PTDi | Valor de Δh PT, en el interior de la curva debido a exceso de peralte. | m |
| Δh PTDa | Valor de Δh PT, en el exterior de la curva debido a exceso de peralte. | m |
| Δh PTIi | Valor de Δh PT, en el interior de la curva debido a insuficiencia de peralte. | m |
| Δh PTIa | Valor de Δh PT, en el exterior de la curva debido a insuficiencia de peralte. | m |
| Δh RV | Desplazamiento perpendicular al plano de rodadura a considerar en la determinación del gálibo de implantación de obstáculos, por inscripción en acuerdos verticales. | m |
| ΔU sr | Diferencia máxima admisible entre los radios de las ruedas de cada bogie (vehículos con bogies) o de cada eje (vehículos con ejes), debido a operaciones de reperfilado. | m |
| η | Giro de la caja de un vehículo parado en vía peraltada, respecto a la perpendicular al plano de rodadura, debido a la flexibilidad de las suspensiones. | (º) |
| η 0 | Giro de la caja de un vehículo con disimetría de construcción o de carga, respecto a la perpendicular al plano de rodadura, debido a la flexibilidad de las suspensiones. | (º) |
| η’ 0 | Disimetría correspondiente a una holgura de las resbaladeras de J=5 mm. Se utiliza en el cálculo de los desplazamientos cuasiestáticos de los vagones equipados con bogies. | (º) |
| θ | Tolerancia de reglaje de la suspensión, utilizada en el cálculo de z’ y z». | rad |
| λ | Disimetría de construcción o de carga de un vehículo, sin considerar la flexibilidad de las suspensiones. Es el ángulo entre la perpendicular al plano de rodadura y la recta que une los centros de gravedad y de rotación. | (º) |
| μ | Coeficiente de adherencia de los ejes del bogie. | |
| σ max | Desviación típica del valor de la fuerza de contacto entre pantógrafo y catenaria. | N |
| τ | Tolerancia de construcción y fijación del pantógrafo, utilizada en el cálculo de z’ y z». | m |
A.3.1 TIPOS
Los gálibos históricos utilizados en las líneas existentes se indican, en función del ancho de vía, en el cuadro A.3.1.
| ANCHO DE VÍA (mm) | GÁLIBO |
|---|---|
| 1668 | GHE16(6) |
| 1435 | GEC14 (Empleado en la línea Madrid-Sevilla) |
| GE14(7) | |
|
Cuadro A.3.1. Gálibos históricos |
|
(6) Definido en la Instrucción de gálibos de 1985
(7) Definido en el documento del GIF “ Criterios técnicos y normas de explotación. Sistema de gálibos ferroviarios en las nuevas líneas de Alta Velocidad”
Con el fin de adaptarlos a la norma europea de gálibos, dichos gálibos se han modificado en los siguientes aspectos:
a) Gálibo del material rodante:
– Desplazamientos verticales a considerar.
– Determinación del gálibo del pantógrafo.
b) Gálibo de las instalaciones fijas:
– Se consideran desplazamientos perpendiculares al plano de rodadura debido a los efectos cuasiestáticos.
– Para el gálibo GHE16 se considera un valor de L = 1,733 m así como un ángulo de disimetría debido al cargamento y al reglaje de las suspensiones idéntico al definido para los gálibos GEA16, GEB16 y GEC16.
c) Gálibo de cargamento:
– Para el gálibo GHE16 son de aplicación las reglas asociadas definidas en el apartado 4.2, la formulación de sus reducciones es igual a la empleada para el gálibo GEC16, al emplear expresiones idénticas para la obtención de los salientes.
A.3.2 CONTORNOS DE REFERENCIA DEL GÁLIBO CINEMÁTICO
A.3.2.1 GHE16
Los contornos de referencia se definen en las figuras 2.29 para las partes altas y 2.33, 2.34 y 2.35 para las partes bajas.
A.3.2.2 GEC14
Este contorno de referencia es una envolvente de los contornos de referencia GHE16 y GC (definido en la norma EN 15273-2:2013) para las partes altas y de los contornos de referencia GEI2 y GI2 (definido en la norma EN 15273-2:2013) para las partes bajas.
Para las partes altas es idéntico al contorno de referencia GEC16, excepto entre 400 mm y 600 mm por encima del plano de rodadura, en el que el semiancho del contorno de referencia es de 1.675 mm. Para las partes bajas se define en la figura A.3.1.
Además, en la figura A.3.2 se incluye un detalle de las partes bajas entre los carriles y sus proximidades.
|
Figura A.3.1. Contorno de referencia del gálibo cinemático GEC14. Partes bajas |
|
|
|
LEYENDA: 1 Anchura máxima teórica del perfil de la pestaña, considerando la posible oblicuidad del eje en la vía. 2 Posición límite efectiva de la cara interna de la rueda, cuando el eje se empuja contra el carril opuesto. 3 Límite de implantación de contracarriles. 4 Posición límite de elementos del vehículo cercanos a las ruedas. 5 Posición límite de la cara externa de la rueda. NOTAS: l = ancho de vía. Cotas válidas para vía horizontal. En acuerdos verticales de radio Rv ≥ 500 m las cotas verticales deben reducirse en un valor Figura A.3.2. Contorno de referencia del gálibo cinemático GEC14. Partes bajas entre los carriles y en sus proximidades |
A.3.2.3 GE14
La figura A.3.3 representa el contorno de referencia para una altura del hilo de contacto de 5,30 m.
|
LEYENDA: 1 Plano de rodadura. 2 Contorno de referencia del pantógrafo del material de tracción eléctrica. Figura A.3.3. Contorno de referencia del gálibo cinemático GE14 para una altura del hilo contacto de 5,30 m |
A.3.3 GÁLIBO DEL MATERIAL RODANTE
A.3.3.1 REGLAS ASOCIADAS
A.3.3.1.1 Desplazamientos verticales
Serán los indicados en el apartado 2.2.2 con las particularidades siguientes:
a) GHE16
Se aplicará lo indicado en el apartado 2.7.2.1.
b) GEC14
Se aplicará lo indicado en el apartado 2.7.2.1.
c) GE14
1) Los desplazamientos verticales a considerar en la determinación de la altura mínima sobre el plano de rodadura, solo se aplicarán a las partes bajas del vehículo situadas a una altura h ≤ 800 mm.
2) Los desplazamientos verticales a considerar en la determinación de la altura máxima sobre el plano de rodadura solo se aplicarán a las partes altas del vehículo situadas a una altura h ≥ 4.850 mm.
A.3.3.1.2 Holgura lateral entre eje de ruedas y vía
a) GHE16
Se aplicará lo indicado en el apartado 2.7.2.2.
b) GEC14
Se aplicará lo indicado en el apartado 2.8.2.2.
c) GE14
Se aplicará lo indicado en el apartado 2.8.2.2.
A.3.3.1.3 Desplazamientos por exceso o insuficiencia de peralte y disimetría
a) GHE16
Se aplicará lo indicado en el apartado 2.7.2.3.
b) GEC14 y GE14
Se obtendrán particularizando las fórmulas de los apartados 2.2.3.3 y 2.2.3.4 para los valores siguientes:
hco = 0,5 m
L = 1,500 m
Io = Do= 0,050 m
Dmax = Imax = 0,160 m
a) Vehículos en general

donde:
![]() es valor absoluto, es decir, que si h<hc se toma hc-h.
es valor absoluto, es decir, que si h<hc se toma hc-h.
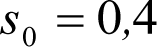
b) Vagones equipados con bogies
∙ Si J ≤ 5 mm:
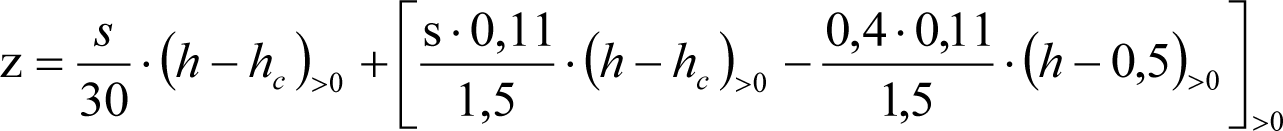
∙ Si J > 5 mm:
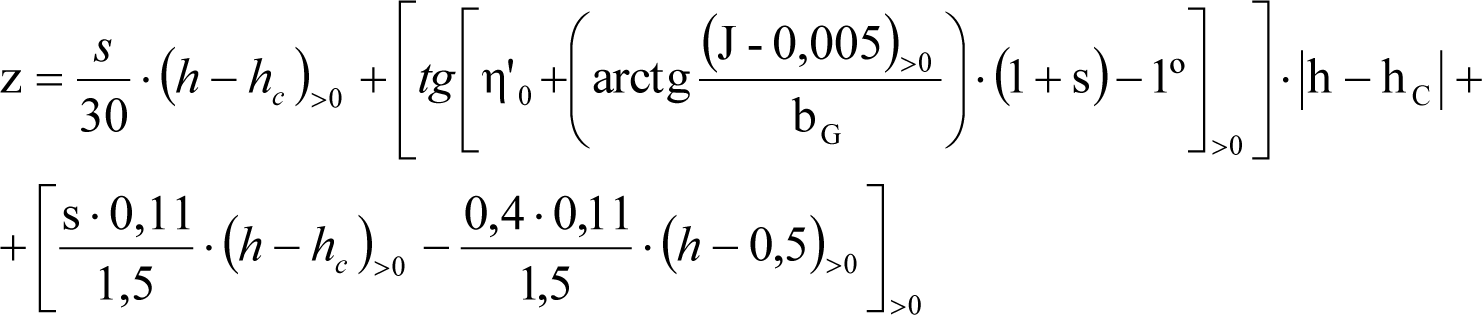
A.3.3.1.4 Salientes
a) GHE16
Se aplicará lo indicado en el apartado 2.7.2.4.
b) GEC14
Se aplicará lo indicado en el apartado 2.8.2.4.
c) GE14
Se aplicará lo indicado en el apartado 2.8.2.4.
A.3.3.2 CÁLCULO DEL PERFIL CONSTRUCTIVO DEL MATERIAL
A.3.3.2.1 Fórmulas de reducción
a) GHE16
Se aplicará lo indicado en el apartado 2.7.3.1.
b) GEC14
Se aplicará lo indicado en el apartado 2.8.3.1.
c) GE14
Se aplicará lo indicado en el apartado 2.8.3.1.
A.3.3.3 CÁLCULO DEL GÁLIBO DE VEHÍCULOS DE CAJA INCLINABLE
a) GHE16
Se aplicará lo indicado en el apartado 2.7.4.
b) GEC14
Se aplicará lo indicado en el apartado 2.8.4.
c) GE14
Se aplicará lo indicado en el apartado 2.8.4.
A.3.3.4 CÁLCULO DEL GÁLIBO DEL PANTÓGRAFO EN POSICIÓN DE CAPTACIÓN
a) GHE16
Se aplicará lo indicado en el apartado 2.7.5.
b) GEC14
Se aplicará lo indicado en el apartado 2.8.5.
c) GE14
Se aplicará lo indicado en el apartado 2.8.5.
A.3.4 GÁLIBO DE IMPLANTACIÓN DE OBSTÁCULOS
A.3.4.1 REGLAS ASOCIADAS
a) GHE16
Se aplicará lo indicado en el apartado 3.10.1.
b) GEC14
Se aplicará lo indicado en el apartado 3.11.1, con s0 = 0,4.
c) GE14
Se aplicará lo indicado en el apartado 3.11.1, con s0 = 0,4.
A.3.4.2. GÁLIBO LÍMITE DE IMPLANTACIÓN DE OBSTÁCULOS
a) GHE16
Se aplicará lo indicado en el apartado 3.10.2.
b) GEC14
Se aplicará lo indicado en el apartado 3.11.2.
c) GE14
Se aplicará lo indicado en el apartado 3.11.2.
A.3.4.3 GÁLIBO DEL PANTÓGRAFO
a) GHE16
Se aplicará lo indicado en el apartado 3.10.4.
b) GEC14
Se aplicará lo indicado en el apartado 3.11.4.
c) GE14
Se aplicará lo indicado en el apartado 3.11.4.
A.3.4.4 GÁLIBO UNIFORME DE IMPLANTACIÓN DE OBSTÁCULOS
a) GHE16
Los contornos de implantación de obstáculos se definen en las figuras A.3.4, A.3.5 y A.3.6.
|
Figura A.3.4. Gálibo uniforme de implantación de obstáculos GHE16. Vía en recta. Partes altas |
|
Figura A.3.5. Gálibo uniforme de implantación de obstáculos GHE16. Vía en curva. Partes altas |
|
Figura A.3.6. Gálibo uniforme de implantación de obstáculos GHE16. Vía en curva de R ≥ 250 m. Partes bajas |
b) GEC14
Los contornos de implantación de obstáculos se definen en las figuras A.3.7 y A.3.8.
|
Figura A.3.7. Gálibo uniforme de implantación de obstáculos GEC14. Vía en recta. Partes altas |
|
Figura A.3.8. Gálibo uniforme de implantación de obstáculos GEC14. Vía en curva. Partes altas |
c) GC14
El contorno de implantación de obstáculos se define en la figura A.3.9.
|
Figura A.3.9. Gálibo uniforme de implantación de obstáculos GC14. Altura del hilo de contacto h=5,30 m |
A.4.1 DEFINICIÓN DE NUEVOS GÁLIBOS
En esta Instrucción se han definido tres nuevos gálibos para ancho ibérico en partes altas (GEA16, GEB16 y GEC16) así como un nuevo gálibo en partes bajas (GEI3), tales que:
– Cumplan las Especificaciones Técnicas de Interoperabilidad correspondientes a los subsistemas de infraestructura, material rodante y energía de los sistemas ferroviarios de alta velocidad y convencional.
– Garanticen la circulación futura del material rodante actualmente existente en la red ferroviaria de interés general.
A.4.2 CONTORNOS DE REFERENCIA DE LOS GÁLIBOS CINEMÁTICOS
A.4.2.1 PARTES ALTAS
Los contornos de referencia de los gálibos cinemáticos GEA16, GEB16 y GEC16 son envolventes del GHE16(8) y de los europeos interoperables GA, GB y GC correspondientes, definidos en la norma EN15273-2:2.013(9).
(8) Definido en la Instrucción de gálibos de 1985
(9) EN 15273-2:2013. Aplicaciones ferroviarias-Gálibos-Parte 2: Gálibo del material rodante
En la figura A.4.1 se representan los contornos de referencia de los gálibos cinemáticos GHE16, GEA16, GEB16 y GEC16, así como de los GA, GB y GC. En la figura A.4.2 se incluye un detalle.
|
Figura A.4.1. Contornos de referencia de los gálibos cinemáticos GHE16, GEA16, GEB16, GEC16, GA, GB y GC |
|
Figura A.4.2. Detalle de los contornos de referencia de los gálibos cinemáticos GHE16, GEA16, GEB16, GEC16, GA, GB y GC |
A.4.2.2 PARTES BAJAS
Los contornos de referencia de los gálibos cinemáticos GEI1 y GEI2 se definen en las figuras 2.33 y 2.34 del apartado 2.7.1.2.
La figura A.4.3 representa los contornos de referencia de los gálibos cinemáticos GEI2, GI2 y GE14.
|
Figura A.4.3. Contornos de referencia de los gálibos cinemáticos GEI2, GI2 y GE14 |
La figura A.4.4 representa los contornos de referencia de los gálibos cinemáticos GEI1 y GI1.
|
Figura A.4.4. Contornos de referencia de los gálibos cinemáticos GEI1 y GI1 |
El contorno de referencia del gálibo cinemático GEI3 definido en la figura 2.35 del apartado 2.7.1.2 es envolvente del GEI2 y del europeo interoperable GI3 definido en la norma EN15273-2:2.013(10).
(10) EN 15273-2:2013. Aplicaciones ferroviarias-Gálibos-Parte 2: Gálibo del material rodante
En la figura A.4.5 se representan los contornos de referencia de los gálibos cinemáticos GEI2, GI2 y GI3. En la figura A.4.6 se incluye un detalle.
|
Figura A.4.5. Contornos de referencia de los gálibos cinemáticos GEI2, GI2 y GI3 |
|
Figura A.4.6. Detalle de los contornos de referencia de los gálibos cinemáticos GEI2, GI2 y GI3 |
A.4.3 CONTORNOS DE REFERENCIA DE LOS GÁLIBOS ESTÁTICOS
A.4.3.1 PARTES ALTAS
Los contornos de referencia de los gálibos estaticos GEA16, GEB16 y GEC16 son envolventes del GHE16(11) y de los europeos interoperables GA, GB y GC correspondientes, definidos en la norma EN15273-2:2.013(12).
(11) Definido en la Instrucción de gálibos de 1985
(12) EN 15273-2:2013. Aplicaciones ferroviarias-Gálibos-Parte 2: Gálibo del material rodante
En la figura A.4.7 se representan las partes altas de los contornos de referencia de los gálibos estáticos GHE16, GEA16, GEB16 y GEC16, así como de los GA, GB y GC. En la figura A.4.8 se incluye un detalle.
|
Figura A.4.7. Partes altas de los contornos de referencia de los gálibos estáticos GHE16, GEA16, GEB16, GEC16, GA, GB y GC |
|
Figura A.4.8. Detalle de las partes altas de los contornos de referencia de los gálibos estáticos GHE16, GEA16, GEB16, GEC16, GA, GB y GC |
A.4.3.2 PARTES BAJAS
Las partes bajas de los contornos de referencia de los gálibos estáticos GEA16, GEB16 y GEC16 son idénticas a las definidas para el gálibo GHE16 en la Instrucción de gálibos de 1.985, y se corresponden con el contorno de referencia GEI1 definido en el apartado 4.4.1.2.
A continuación se incluyen tres ejemplos de aplicación de las fórmulas de reducción expuestas en el capítulo 2 para la obtención del gálibo del material rodante GHE16.
A.5.1 CÁLCULO DE UNA LOCOMOTORA
Las características geométricas de la locomotora se definen en la figura A.5.1 (cotas expresadas en milímetros).
|
Figura A.5.1. Características geométricas de la locomotora. |
Características de la locomotora:
| a = 10,390m | p = 2,600m | d = 1,643m | q = 0,012m | w = 0,038m |
| s = 0,1166 | hc = 1,045m | ηo<1.º | μ>0,2 | na = 4,059m |
Se aplican las fórmulas de reducción para material motor definidas en el apartado 2.7.3.1.1, casos c) y d), correspondientes a holguras constantes:
 .
.
a) En secciones internas del vehículo, y en particular, para la sección central:
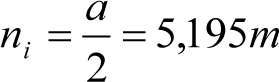
Como: 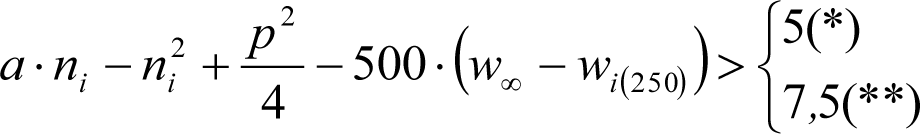 , la máxima reducción se da en curva y la fórmula de reducción será:
, la máxima reducción se da en curva y la fórmula de reducción será:

| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
donde:

por lo que se considera xi = 0.
Los desplazamientos cuasiestáticos serán:

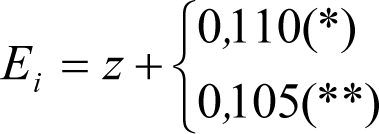
b) En secciones externas del vehículo, y en particular, para la sección extrema:
 .
.
Como: 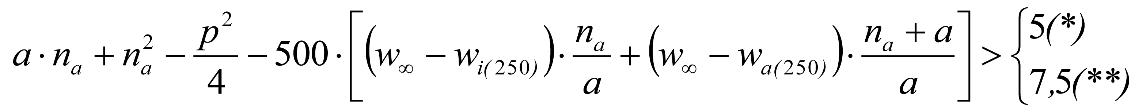 , la máxima reducción se da en curva y la fórmula de reducción será:
, la máxima reducción se da en curva y la fórmula de reducción será:
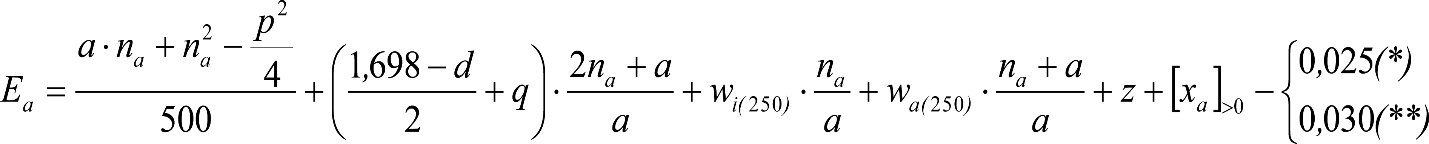
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
donde:

por lo que se considera xa = 0.

Las reducciones Ei y Ea y el semiancho disponible para el perfil constructivo del material, a las alturas características del contorno de referencia cinemático, se resumen en el cuadro A.5.1.
| h (m) | z (m) | Semiancho contorno de referencia (m) | Ei (m) | Semiancho disponible (m) | Ea (m) | Semiancho disponible (m) |
|---|---|---|---|---|---|---|
| 4,330 | 0,011 | 0,800 | 0,116 | 0,684 | 0,233 | 0,567 |
| 4,100 | 0,010 | 1,250 | 0,115 | 1,135 | 0,232 | 1,018 |
| 3,700 | 0,009 | 1,580 | 0,114 | 1,466 | 0,231 | 1,349 |
| 3,320 | 0,008 | 1,720 | 0,113 | 1,607 | 0,230 | 1,490 |
| 1,150 | 0 | 1,720 | 0,105 | 1,615 | 0,222 | 1,498 |
| 1,695 | 1,590 | 1,473 | ||||
| 0,600 | 0 | 1,695 | 0,105 | 1,590 | 0,222 | 1,473 |
| 1,675 | 1,570 | 1,453 | ||||
| 0,400 | 0 | 1,675 | 0,110 | 1,565 | 0,227 | 1,448 |
| 1,637 | 1,527 | 1,410 | ||||
|
Cuadro A.5.1. Resultados del cálculo del gálibo del material rodante GHE16 de una locomotora |
||||||
Además, para definir el gálibo del material rodante en partes altas y bajas, se deben reducir las alturas del contorno de referencia de acuerdo con lo indicado en el apartado 2.2.2.
A.5.2 CÁLCULO DE UN VAGÓN CISTERNA
Las características geométricas del vagón cisterna se definen en la figura A.5.2 (cotas expresadas en milímetros).
|
Figura A.5.2. Características geométricas del vagón cisterna. |
Características del vagón cisterna:
| a = 11,700m | p=1,800m | d = 1,643m | q = 0,0115m | w = 0 |
| bG = 0,850m | s = 0,130 | hc = 0,500m | η'o=1.º | J = 0,012m |
| na = 1,890m |
Se aplican las fórmulas de reducción para material remolcado definidas en el apartado 2.7.3.1.2, casos e) y f), correspondientes vagones con bogies y holguras constantes.
a) En secciones internas del vehículo, y en particular, para la sección central: 
Como: 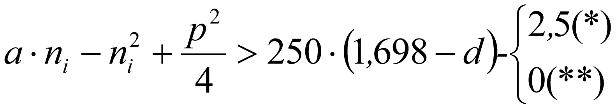 , la máxima reducción se da en curva y la fórmula de reducción será:
, la máxima reducción se da en curva y la fórmula de reducción será:
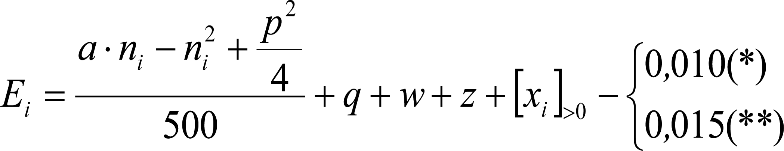
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
donde:
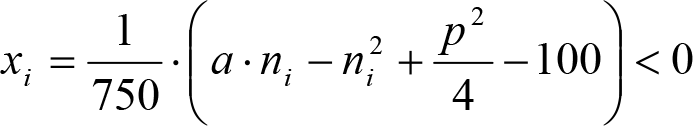
por lo que se considera xi = 0.
Los desplazamientos cuasiestáticos, para el caso en que J>5 mm, serán:

b) En secciones externas del vehículo, y en particular, para la sección extrema:
n= na = 1,89m:
Como: , la máxima reducción se da en curva y la fórmula de reducción será:
, la máxima reducción se da en curva y la fórmula de reducción será:

| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
donde:
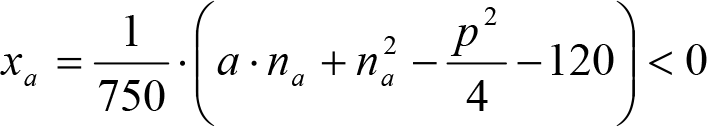
por lo que se considera xa = 0.

Las reducciones Ei y Ea y el semiancho disponible para el perfil constructivo del material, a las alturas características del contorno de referencia cinemático, se resumen en el cuadro A.5.2.
|
h (m) |
z (m) | Semiancho contorno de referencia (m) | Ei (m) | Semiancho disponible (m) | Ea (m) | Semiancho disponible (m) |
|---|---|---|---|---|---|---|
| 4,330 | 0,050 | 0,800 | 0,117 | 0,683 | 0,116 | 0,684 |
| 4,100 | 0,047 | 1,250 | 0,114 | 1,136 | 0,113 | 1,137 |
| 3,700 | 0,042 | 1,580 | 0,109 | 1,471 | 0,108 | 1,472 |
| 3,320 | 0,037 | 1,720 | 0,104 | 1,616 | 0,103 | 1,617 |
| 1,150 | 0,008 | 1,720 | 0,075 | 1,645 | 0,074 | 1,646 |
| 1,695 | 1,62 | 1,621 | ||||
| 0,600 | 0,001 | 1,695 | 0,068 | 1,627 | 0,067 | 1,628 |
| 1,675 | 1,607 | 1,608 | ||||
| 0,400 | 0 | 1,675 | 0,072 | 1,603 | 0,072 | 1,603 |
| 1,637 | 1,565 | 1,565 | ||||
|
Cuadro A.5.2. Resultados del cálculo del gálibo del material rodante GHE16 de un vagón cisterna |
||||||
Además, para definir el gálibo del material rodante en partes altas y bajas, se deben reducir las alturas del contorno de referencia de acuerdo con lo indicado en el apartado 2.2.2.
A.5.3 CÁLCULO DE UN VEHÍCULO AUTOPROPULSADO
Las características geométricas del vehículo autopropulsado se definen en la figura A.5.3 (cotas expresadas en milímetros).
|
Figura A.5.3. Características geométricas del vehículo autopropulsado. |
Características del vehículo autopropulsado:
| a = 17,750m | d = 1,643m | w =0,040m | p = 2,500m | q = 0,005m |
| s = 0,163 | hc = 0,577m | w’ =0,040m | p’ = 2,500m | ηo<1.º |
| na (lado bogie motor)= 2,75m | na (lado bogie portador)= 2,75m | |||
Se aplican las fórmulas de reducción para material autopropulsado definidas en el apartado 2.7.3.1.4.
En este caso las holguras son constantes:
wi(R) = wa(R) = w∞= w’i(R) = w’a(R) = w’∞ = constante.
a) En secciones internas del vehículo, y en particular, para la sección central: 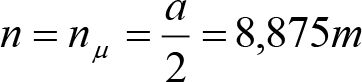
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
En recta:
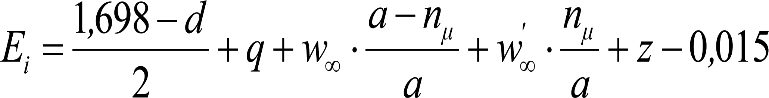
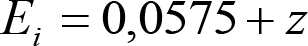
En curva:
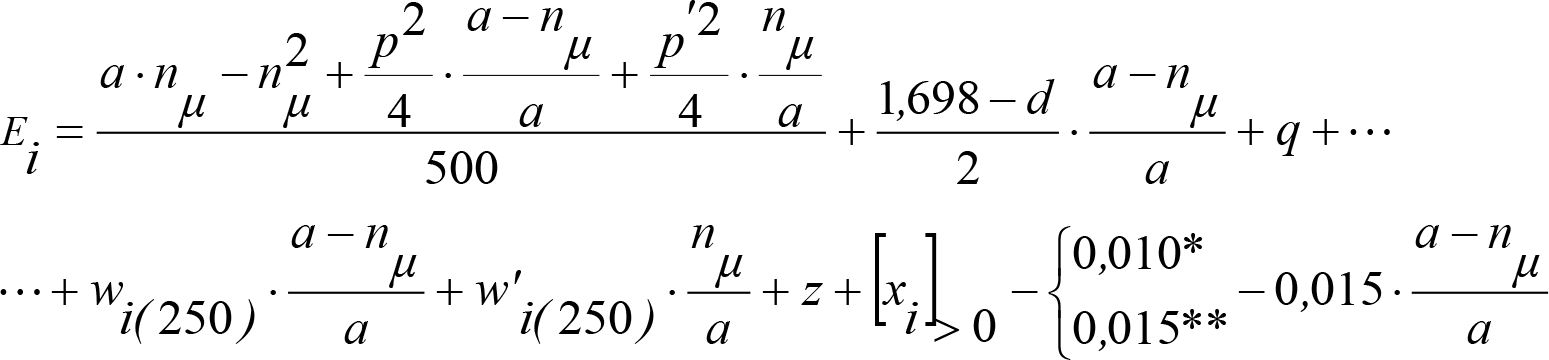
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
donde:
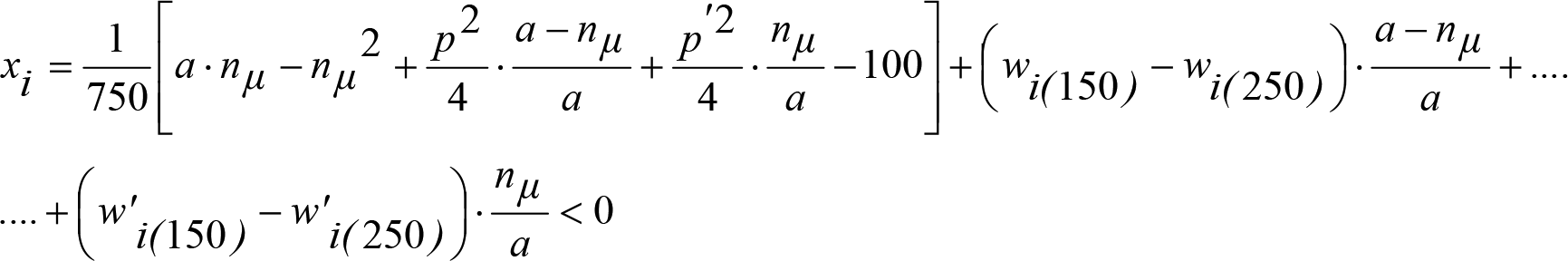
por lo que se considera xi = 0.

Por tanto, la situación más desfavorable se produce en curva.
Los desplazamientos cuasiestáticos serán:

Las reducciones Ei y el semiancho disponible para el perfil constructivo del material, a las alturas características del contorno de referencia cinemático, se resumen en el cuadro A.5.3.
| h (m) | z (m) | Semiancho contorno de referencia (m) | Ei (m) | Semiancho disponible (m) |
|---|---|---|---|---|
| 4,330 | 0,017 | 0,800 | 0,204 | 0,596 |
| 4,100 | 0,015 | 1,250 | 0,202 | 1,048 |
| 3,700 | 0,015 | 1,580 | 0,202 | 1,378 |
| 3,320 | 0,013 | 1,720 | 0,200 | 1,520 |
| 1,150 | 0,003 | 1,720 | 0,190 | 1,530 |
| 1,695 | 1,505 | |||
| 0,600 | 0 | 1,695 | 0,187 | 1,508 |
| 1,675 | 1,488 | |||
| 0,400 | 0 | 1,675 | 0,192 | 1,483 |
| 1,637 | 1,445 | |||
|
Cuadro A.5.3. Resultados del cálculo del gálibo del material rodante GHE16 de un vehículo autopropulsado. Secciones internas. |
||||
Además, para definir el gálibo del material rodante en partes altas y bajas, se deben reducir las alturas del contorno de referencia de acuerdo con lo indicado en el apartado 2.2.2.
b) En secciones externas del vehículo del lado bogie motor, y en particular, para la sección extrema:
n= na =2,75 m:
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
En recta:

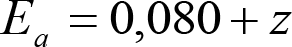
En curva:
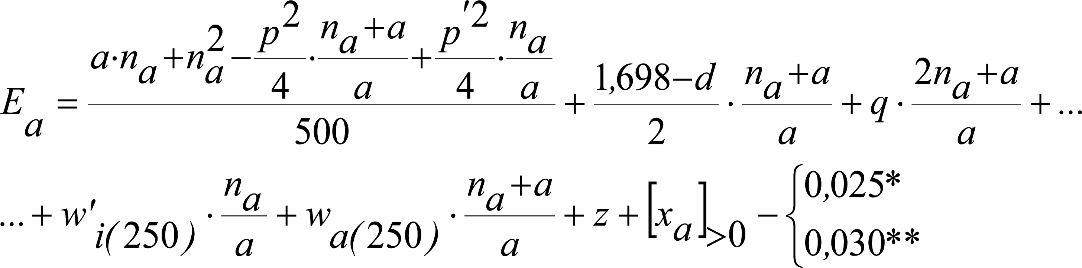
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
donde:
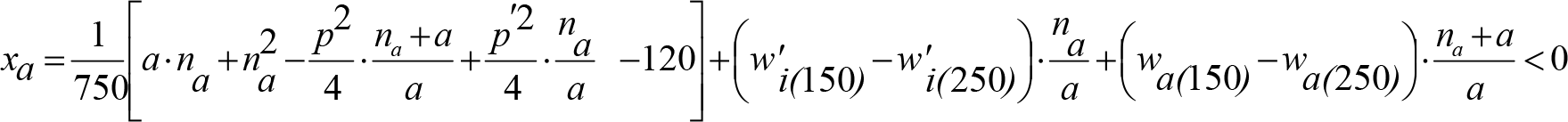
por lo que se considera xa = 0.
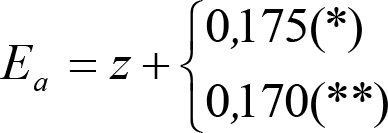
Por tanto, la situación más desfavorable se produce en curva.
Las reducciones Ea del lado bogie motor y el semiancho disponible para el perfil constructivo del material, a las alturas características del contorno de referencia cinemático, se resumen en el cuadro A.5.4.
| h (m) | z (m) | Semiancho contorno de referencia (m) | Ea (m) | Semiancho disponible (m) |
|---|---|---|---|---|
| 4,330 | 0,017 | 0,800 | 0,187 | 0,613 |
| 4,100 | 0,015 | 1,250 | 0,185 | 1,065 |
| 3,700 | 0,015 | 1,580 | 0,185 | 1,395 |
| 3,320 | 0,013 | 1,720 | 0,183 | 1,537 |
| 1,150 | 0,003 | 1,720 | 0,173 | 1,547 |
| 1,695 | 1,522 | |||
| 0,600 | 0 | 1,695 | 0,170 | 1,525 |
| 1,675 | 1,505 | |||
| 0,400 | 0 | 1,675 | 0,175 | 1,500 |
| 1,637 | 1,462 | |||
|
Cuadro A.5.4. Resultados del cálculo del gálibo del material rodante GHE16 de un vehículo autopropulsado. Secciones externas lado bogie motor. |
||||
c) En secciones externas del vehículo del lado bogie portador, y en particular, para la sección extrema:
n= na =2,75 m:
La reducción a aplicar será la máxima que se obtenga entre considerar recta o curva.
En recta:
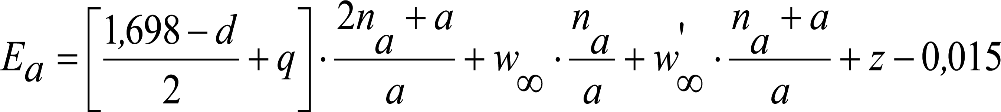
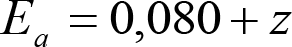
En curva:
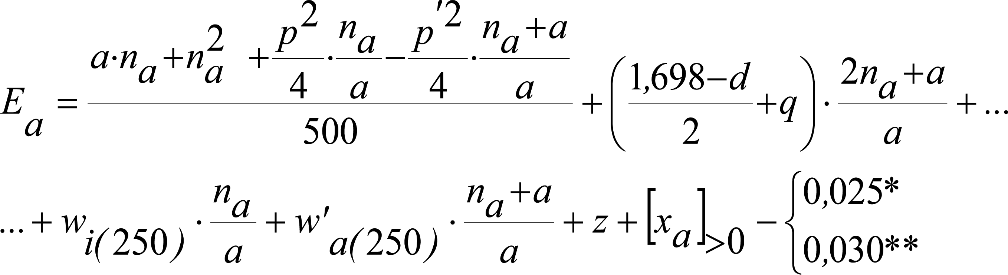
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
donde:
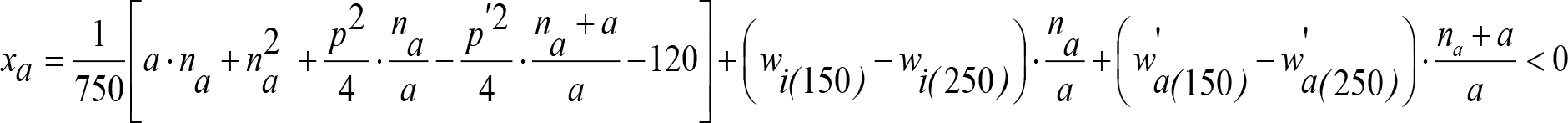
por lo que se considera xa = 0.

Por tanto, la situación más desfavorable se produce en curva.
Las reducciones Ea del lado bogie portador y el semiancho disponible para el perfil constructivo del material, a las alturas características del contorno de referencia cinemático, se resumen en el cuadro A.5.5.
| h (m) | z (m) | Semiancho contorno de referencia (m) | Ea (m) | Semiancho disponible (m) |
|---|---|---|---|---|
| 4,330 | 0,017 | 0,800 | 0,192 | 0,608 |
| 4,100 | 0,015 | 1,250 | 0,190 | 1,060 |
| 3,700 | 0,015 | 1,580 | 0,190 | 1,390 |
| 3,320 | 0,013 | 1,720 | 0,188 | 1,532 |
| 1,150 | 0,003 | 1,720 | 0,178 | 1,542 |
| 1,695 | 1,517 | |||
| 0,600 | 0 | 1,695 | 0,175 | 1,520 |
| 1,675 | 1,500 | |||
| 0,400 | 0 | 1,675 | 0,180 | 1,495 |
| 1,637 | 1,457 | |||
|
Cuadro A.5.5. Resultados del cálculo del gálibo del material rodante GHE16 de un vehículo autopropulsado. Secciones externas lado bogie portador. |
||||
En este anejo se incluye un ejemplo de cálculo de un vehículo de caja inclinable (VCI) con sistema activo y otro con sistema pasivo, para la obtención del gálibo del material rodante GHE16.
| hco = 0,5m | L = 1,733 m | Io = 0,050m | so = 0,4 | l= 1,698m |
A.6.1 CÁLCULO DE UN VCI CON SISTEMA ACTIVO
Se considera el caso de un TRD Basculante.
A.6.1.1 CARACTERÍSTICAS DEL SISTEMA DE INCLINACIÓN DE LA CAJA
Cuando el VCI circula sobre una vía en curva con una Ip>0, y después de medir determinados parámetros (velocidad, variación del peralte y radio de la curva), el sistema impone un giro, β, a la caja (figura A.6.1), que es independiente de la inclinación debida a la flexibilidad de las suspensiones.
En los TRD Basculantes, este mecanismo de giro impuesto por el sistema se sitúa entre la suspensión primaria y la secundaria, lo que implica considerar la flexibilidad de cada una de ellas, en vez de la global del sistema, en el cálculo de los desplazamientos cuasiestáticos del apartado A.6.1.3.
Las características del sistema de inclinación activa para este tipo de vehículos se indican en la figura A.6.1.
|
ho: altura del centro de rotación de la caja impuesto por el sistema. β’: ángulo de inclinación de la caja impuesto por el sistema. Es función de la insuficiencia de peralte Ip. |
– Para v<40 km/h el sistema de inclinación de la caja no actúa: β =0. – Los desplazamientos transversales debidos a la inclinación de la caja β impuesta por el sistema son: – z*>0 en el lado interior de la curva, ya que los desplazamientos se aproximan al contorno de referencia interior. – z*<0 en el lado exterior de la curva, ya que los desplazamientos se alejan del contorno de referencia exterior. |
|
Figura A.6.1. Características del sistema de inclinación activo |
|
A.6.1.2 PARÁMETROS DE CÁLCULO
Características del vehículo:
| a = 17,734m | p = 2,700m | d = 1,643m | q = 0,001m |
| w∞= 0,050m | wi(250) = wi(150) =0,050m | wa(250) = wi(150) =0,050m | s= 0,260 |
| s1 = 0,069285 | s2 = 0,190726 | anccaja = 0,650 m/s2 | ancvía = 1,800 m/s2 |
| hccaja = 0,815m | hcvía = 0,450 m | β =6.º para I p=0,318m | ho = 1,600m |
| Ic = 0,115m | ηo < 1.º | hc =0,7177m | na = 3,000m |
| Todos los bogies son motores. | |||
Además, se adoptan las simplificaciones siguientes:
– s y hc se consideran constantes para todas las situaciones operativas a verificar (aunque en realidad varíen).
– Los desplazamientos verticales debidos a la inclinación de la caja β impuesta por el sistema, se consideran nulos (aunque en realidad no lo sean).
En consecuencia, los valores numéricos que se obtengan, solo serán una aproximación a la realidad.
Los valores intermedios, Ip’ e Ic’, de Ip y de Ic, deberán cumplir:
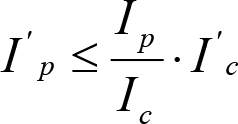
A.6.1.3 COMPROBACIÓN DE LA SITUACIÓN 1: VEHÍCULO CIRCULANDO EN CURVA CON INSUFICIENCIA DE PERALTE MÁXIMA
Como todos los bogies son motores, se aplican las fórmulas de reducción para material motor definidas en el apartado 2.7.3.1.1, casos c) y d), correspondientes a holguras constantes, sustituyendo las holguras laterales de la fórmula por las definidas en el cuadro 2.5 del apartado 2.4.3.1 (con sus correspondientes factores de desplazamiento), y los desplazamientos cuasiestáticos z, por el término 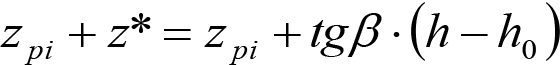 definido en el apartado 2.4.3.4.1.
definido en el apartado 2.4.3.4.1.
| Se sustituye | por | |
|---|---|---|
| Secciones internas |
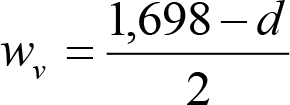
|
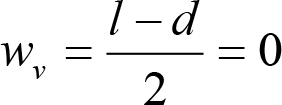
|
| q | 0 | |
|
|
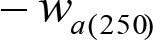
|
|
| z |
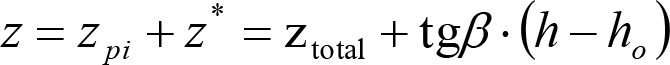
|
|
| Secciones externas |
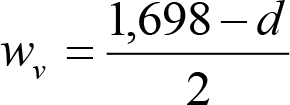
|
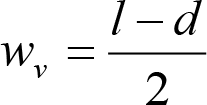
|
| q | q | |
|
|
0 | |
|
|
|
|
| z |

|
a) Lado interior de la curva (secciones internas):
Para la sección central: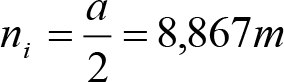
Como: 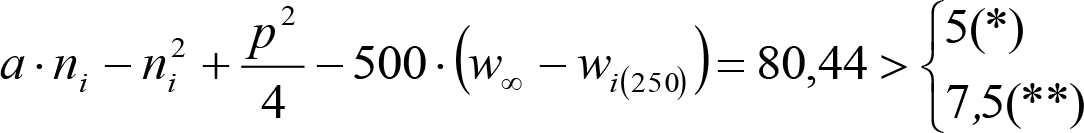 , la máxima reducción se da en curva y la fórmula de reducción será:
, la máxima reducción se da en curva y la fórmula de reducción será:
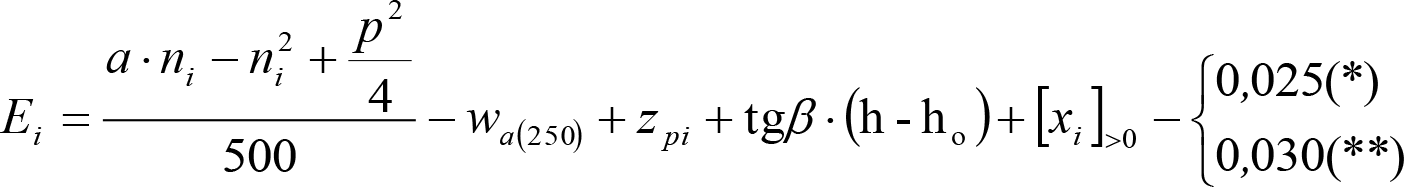
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
donde:  , por lo que se considera xi = 0.
, por lo que se considera xi = 0.
El valor de zpi se obtendrá a partir de las flexibilidades de la suspensión primaria (s1) y de la secundaria (s2), mediante la expresión del apartado 2.4.3.2:

Las reducciones Ei para las diferentes alturas características del contorno de referencia cinemático, así como el semiancho disponible para el perfil constructivo del material, se resumen en el cuadro A.6.1.
b) Lado exterior de la curva (secciones externas):
Para la sección extrema: n = na = 3m.
Como:  , la máxima reducción se da en curva y la fórmula de reducción será:
, la máxima reducción se da en curva y la fórmula de reducción será:

| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
donde: 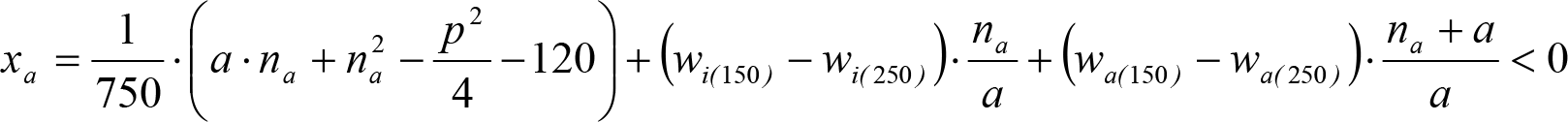 , por lo que se considera xa = 0.
, por lo que se considera xa = 0.
El valor de zpa se obtendrá a partir de las flexibilidades de la suspensión primaria (s1) y de la secundaria (s2), mediante la expresión del apartado 2.4.3.2:
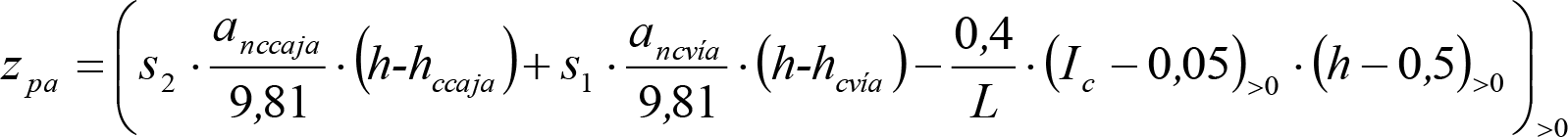
Las reducciones Ea para las diferentes alturas características del contorno de referencia cinemático, así como el semiancho disponible para el perfil constructivo del material, se resumen en el cuadro A.6.1.
| h (m) | zpi (m) | zpa (m) | Semiancho contorno de referencia (m) | Ei (m) | Semiancho disponible (m) | Ea (m) | Semiancho disponible (m) |
|---|---|---|---|---|---|---|---|
| 4,330 | -0,094 | 0,037 | 0,800 | 0,274 | 0,526 | 0(-0,063) | 0,800 |
| 4,100 | -0,088 | 0,034 | 1,250 | 0,256 | 0,994 | 0(-0,041) | 1,250 |
| 3,700 | -0,078 | 0,030 | 1,580 | 0,224 | 1,356 | 0(-0,04) | 1,580 |
| 3,320 | -0,068 | 0,026 | 1,720 | 0,194 | 1,526 | 0,033 | 1,687 |
| 1,150 | -0,013 | 3,420*10-3 | 1,720 | 0,020 | 1,700 | 0,238 | 1,482 |
| 1,150 | -0,013 | 3,420*10-3 | 1,695 | 0,020 | 1,675 | 0,238 | 1,457 |
| 0,600 | 0,001 | 0(-2,304*10-3) | 1,695 | 0(-0,023) | 1,695 | 0,290 | 1,405 |
| 0,600 | 0,001 | 0(-2,304*10-3) | 1,675 | 0(-0,023) | 1,675 | 0,290 | 1,385 |
| 0,400 | 0,006 | 0(-5,88*10-3) | 1,675 | 0(-0,039) | 1,675 | 0,313 | 1,362 |
| 0,400 | 0,006 | 0(-5,88*10-3) | 1,637 | 0(-0,039) | 1,637 | 0,313 | 1,324 |
|
Cuadro A.6.1. Resultados del cálculo del gálibo del material rodante GHE16 de un VCI con sistema activo. SITUACIÓN 1. |
|||||||
A.6.1.4 COMPROBACIÓN DE LA SITUACIÓN 2: VEHÍCULO DETENIDO EN CURVA
En este caso el sistema de basculación no está activo. Las fórmulas serán las correspondientes a los vehículos convencionales indicadas en el apartado 2.7.3.1.1, casos c) y d), correspondientes a holguras constantes.
a) Lado interior de la curva (secciones internas):
Para la sección central: 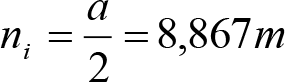
Como: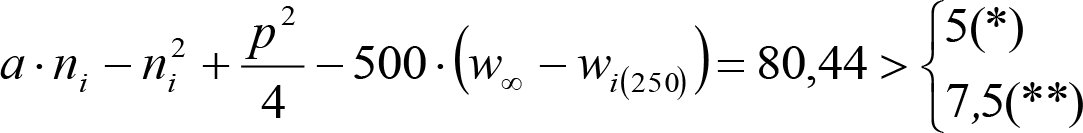 , la máxima reducción se da en curva y la fórmula de reducción será:
, la máxima reducción se da en curva y la fórmula de reducción será:

| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
donde: , por lo que se considera xi= 0.
, por lo que se considera xi= 0.
Los desplazamientos cuasiestáticos serán:

Y las reducciones:

Las reducciones Ei para las diferentes alturas características del contorno de referencia cinemático, así como el semiancho disponible para el perfil constructivo del material, se resumen en el cuadro A.6.2.
b) Lado exterior de la curva (secciones externas):
Para la sección extrema: n = na = 3m
Como: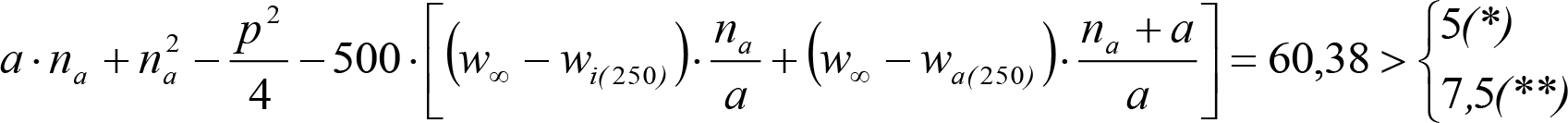 , la máxima reducción se da en curva y la fórmula de reducción será:
, la máxima reducción se da en curva y la fórmula de reducción será:
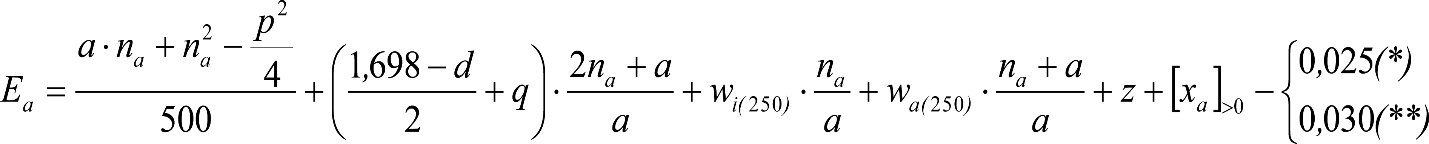
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
donde:  , por lo que se considera xa= 0.
, por lo que se considera xa= 0.
Los desplazamientos cuasiestáticos serán:

Y las reducciones:

Las reducciones Ea para las diferentes alturas características del contorno de referencia cinemático, así como el semiancho disponible para el perfil constructivo del material, se resumen en el cuadro A.6.2.
| h (m) | zp(m) | Semiancho contorno de referencia (m) | Ei(m) | Semiancho disponible (m) | Ea(m) | Semiancho disponible (m) |
|---|---|---|---|---|---|---|
| 4,330 | 0,026 | 0,800 | 0,235 | 0,565 | 0,222 | 0,578 |
| 4,100 | 0,025 | 1,250 | 0,234 | 1,016 | 0,221 | 1,029 |
| 3,700 | 0,022 | 1,580 | 0,231 | 1,349 | 0,218 | 1,362 |
| 3,320 | 0,019 | 1,720 | 0,228 | 1,492 | 0,215 | 1,505 |
| 1,150 | 0,003 | 1,720 | 0,212 | 1,508 | 0,199 | 1,521 |
| 1,150 | 0,003 | 1,695 | 0,212 | 1,483 | 0,199 | 1,496 |
| 0,600 | 0 | 1,695 | 0,209 | 1,486 | 0,196 | 1,499 |
| 0,600 | 0 | 1,675 | 0,209 | 1,466 | 0,196 | 1,479 |
| 0,400 | 0 | 1,675 | 0,214 | 1,461 | 0,201 | 1,474 |
| 0,400 | 0 | 1,637 | 0,214 | 1,423 | 0,201 | 1,436 |
|
Cuadro A.6.2. Resultados del cálculo del gálibo del material rodante GHE16 de un VCI con sistema activo. SITUACIÓN 2. |
||||||
A.6.2 CÁLCULO DE UN VCI CON SISTEMA PASIVO
Se considera el caso de un TALGO Pendular.
|
Figura A.6.2. Esquema de coches del TALGO Pendular |
A.6.2.1 CARACTERÍSTICAS DE LOS VEHÍCULOS
Las características del tren TALGO son las siguientes:
a) Está constituido por coches de poca longitud, articulados entre ellos, constituyendo ramas homogéneas.
b) Cada coche dispone de unas balonas situadas por encima del centro de gravedad de la caja que permiten, al paso por curvas, la pendulación natural de dicha caja reduciendo una parte de la aceleración centrífuga no compensada. El centro de balanceo de la caja está situado a la altura del centro de las balonas de la suspensión.
c) Los elementos de rodadura están integrados en la estructura que, en su parte superior, soporta las balonas y la caja. Dicha estructura se sitúa en la unión entre coches. Los coches extremos tienen una estructura adicional.
d) Las ruedas no están unidas por ejes, sino que giran independientemente y son guiadas con un ángulo de ataque casi nulo.
e) Cada coche dispone de dos topes laterales entre la caja y la estructura. Uno situado en la parte superior de la caja y el otro en la inferior (figura 2.20).
A.6.2.2 CARACTERÍSTICAS DEL SISTEMA DE INCLINACIÓN DE LA CAJA
Las características del sistema de inclinación para estos vehículos se indican en la figura 2.20.
Cuando el vehículo está parado o sometido a un exceso de peralte con v<60km/h, el sistema de suspensión mantiene la caja paralela al plano de la vía, es decir s=0.
En el cálculo de gálibo deben comprobarse las hipótesis de contacto con los topes superior e inferior, eligiendo el desplazamiento más desfavorable. Para ello, se consideran los parámetros siguientes:
WS = holgura entre la caja y la estructura del vehículo en el tope lateral superior.
WI = holgura entre la caja y la estructura del vehículo en el tope lateral inferior.
hs = altura del tope superior del sistema de basculación de la caja, respecto al plano de rodadura.
hi = altura del tope inferior del sistema de basculación de la caja, respecto al plano de rodadura.
En los vehículos TALGO y en los vehículos clásicos no se consideran las posibles rotaciones de la caja posteriores al contacto con el tope, ya que no se dan en explotación normal.
A.6.2.3 COMPROBACIÓN DE LA SITUACIÓN 1: VEHÍCULO CIRCULANDO EN CURVA CON INSUFICIENCIA DE PERALTE MÁXIMA
En este caso, el giro de la caja se produce hacia el lado exterior de la curva. La zona crítica para el gálibo se sitúa en el contorno exterior y para las partes bajas del vehículo.
En los coches intermedios, debido a la disposición de ruedas en los extremos, todas las secciones de la caja serán internas (Ei). Además, las más desfavorables serán las situadas junto a los extremos (figura A.6.3).
|
Figura A.6.3. Vista en planta de los desplazamientos de la caja de un coche TALGO intermedio a una altura h<hc |
Para los coches extremos, la sección interna (Ei) más desfavorable estará situada igualmente en el extremo próximo al coche contiguo, mientras que la externa (Ea).más desfavorable será la situada en voladizo, en el extremo opuesto.
A.6.2.3.1 Parámetros de cálculo
Al tratarse de vehículos sin bogies: p=0.
El vehículo se apoya sobre el carril exterior de la curva, por lo que las holguras wv=(l-d)/2, q y w tienen signo positivo.
Además, se adoptan las simplificaciones siguientes:
– Las holguras de topes se consideran independientes del radio de la curva.
– Aunque los valores de xi y xa se calculan aplicando las fórmulas generales del apartado 2.4.3.4.2, en este caso, debido a los reducidos valores del empate, se tomarán xi = xa =0.
En consecuencia, los valores numéricos que se obtengan, solo serán una aproximación a la realidad.
Se consideran los parámetros siguientes:
| COCHE INTERMEDIO | ||||
|---|---|---|---|---|
| a =13,140 m | s = 0,250 | Ip = 0,212 m | Ic = 0,115 m | hi = 0,530 m |
| hs = 2,654 m | hc = 2,654 m | q = 0,001 m | WI = 0,154 m | WS = 0,085 m |
| d = 1,643 m | ηo < 1.º | na = 2,63 m | ||
|
Figura A.6.4. Características geométricas de un coche intermedio |
| COCHE EXTREMO | |||||
|---|---|---|---|---|---|
| a = 8,970 m | s = 0,250 | Ip = 0,212 m | Ic = 0,115 m | hi = 0,530 m | |
| hs = 2,135 m | hc = 2,135 m | q = 0,001 m | WI = 0,101 m | WS = 0,085 m | |
| d = 1,643 m | ηo < 1.º | ||||
|
Figura A.6.5. Características geométricas de un coche extremo |
A.6.2.3.2 Fórmulas de aplicación
Para las reducciones en secciones internas Ei (coches intermedios o extremos) y externas Ea (coches extremos) se utilizan las fórmulas siguientes, definidas en el apartado 2.4.3.4.2:
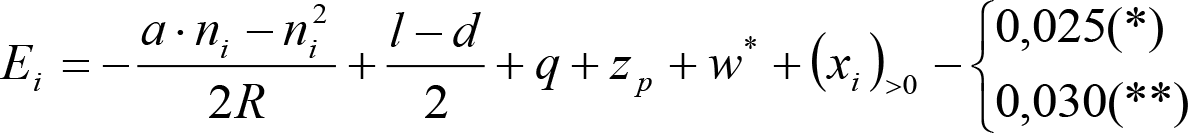
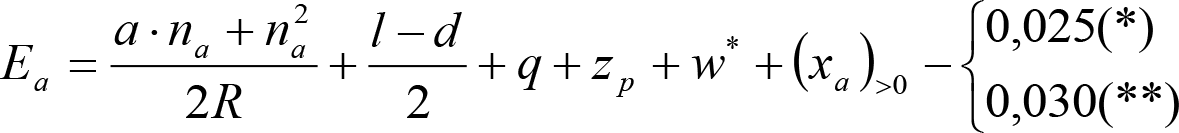
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
donde, según el apartado 2.4.3.2.2, el valor de zp para el lado exterior de la curva será:
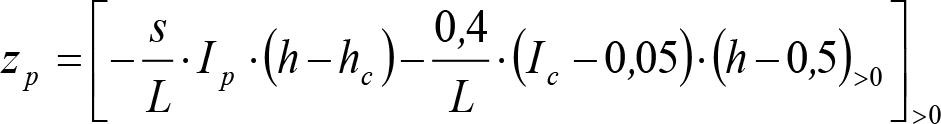
A.6.2.3.3 Aplicación a un coche intermedio
Los resultados son los siguientes:

| Coche intermedio | n i =1,375 m | n i =0 | ||||
|---|---|---|---|---|---|---|
| h (m) | zp (m) | Semiancho contorno de referencia (m) | Ei (m) | Semiancho disponible (m) | Ei (m) | Semiancho disponible (m) |
| 4,330 | 0(-0,108) | 0,800 | 0,051 | 0,749 | 0,083 | 0,717 |
| 4,100 | 0(-0,098) | 1,250 | 0,051 | 1,199 | 0,083 | 1,167 |
| 3,700 | 0(-0,080) | 1,580 | 0,051 | 1,529 | 0,083 | 1,497 |
| 3,320 | 0(-0,062) | 1,720 | 0,051 | 1,669 | 0,083 | 1,637 |
| 1,150 | 0,036 | 1,720 | 0,087 | 1,633 | 0,120 | 1,600 |
| 1,150 | 0,036 | 1,695 | 0,087 | 1,608 | 0,120 | 1,575 |
| 0,600 | 0,061 | 1,695 | 0,112 | 1,583 | 0,145 | 1,550 |
| 0,600 | 0,061 | 1,675 | 0,112 | 1,563 | 0,145 | 1,530 |
| 0,400 | 0,069 | 1,675 | 0,120 | 1,555 | 0,152 | 1,523 |
| 0,400 | 0,069 | 1,637 | 0,120 | 1,517 | 0,152 | 1,485 |
|
Cuadro A.6.3. Resultados del cálculo del gálibo del material rodante GHE16 de un VCI con sistema pasivo. SITUACIÓN 1. Coche intermedio. |
||||||
A.6.2.3.4 Aplicación a un coche extremo
Los resultados son los siguientes:
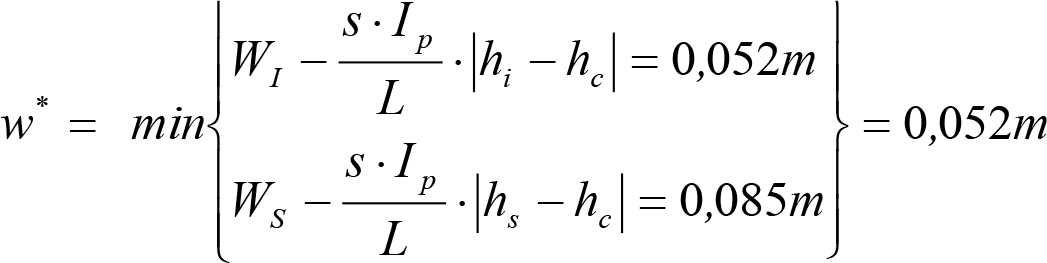
| Coche extremo | n i =1,375 m | n a =2,63m | ||||
|---|---|---|---|---|---|---|
| h (m) | zp (m) | Semiancho contorno de referencia (m) | Ei (m) | Semiancho disponible (m) | Ea (m) | Semiancho disponible (m) |
| 4,330 | 0(-0,124) | 0,800 | 0,029 | 0,771 | 0,117 | 0,683 |
| 4,100 | 0(-0,114) | 1,250 | 0,029 | 1,221 | 0,117 | 1,133 |
| 3,700 | 0(-0,095) | 1,580 | 0,029 | 1,551 | 0,117 | 1,463 |
| 3,320 | 0(-0,078) | 1,720 | 0,029 | 1,691 | 0,117 | 1,603 |
| 1,150 | 0,020 | 1,720 | 0,050 | 1,670 | 0,132 | 1,588 |
| 1,150 | 0,020 | 1,695 | 0,050 | 1,645 | 0,132 | 1,563 |
| 0,600 | 0,045 | 1,695 | 0,075 | 1,620 | 0,157 | 1,538 |
| 0,600 | 0,045 | 1,675 | 0,075 | 1,600 | 0,157 | 1,518 |
| 0,400 | 0,053 | 1,675 | 0,082 | 1,593 | 0,164 | 1,511 |
| 0,400 | 0,053 | 1,637 | 0,082 | 1,555 | 0,164 | 1,473 |
|
Cuadro A.6.4. Resultados del cálculo del gálibo del material rodante GHE16 de un VCI con sistema pasivo. SITUACIÓN 1. Coche extremo. |
||||||
A.6.2.4 COMPROBACIÓN DE LA SITUACIÓN 2: VEHÍCULO PARADO EN CURVA CON PERALTE
Se comprueba el gálibo en el lado interior de la curva para la sección media de un vehículo intermedio, que es el caso más desfavorable.
A.6.2.4.1 Parámetros de cálculo
El valor de w depende del peralte. Para una curva de R=250 m y peralte de 0,150 m, se toma w =0,057 m (*).
Se consideran los parámetros siguientes:
| COCHE INTERMEDIO | ||||
|---|---|---|---|---|
| a =13,140 m | s =0 | Ip =0,212 m | Ic =0,115 m | hi =0,530 m |
| hs =2,654 m | hc =2,654 m | q =0,001 m | wi(250)=0,057m (*) | d =1,643 m |
A.6.2.4.2 Fórmulas de aplicación
Para el cálculo de las reducciones Ei se utiliza la fórmula siguiente:
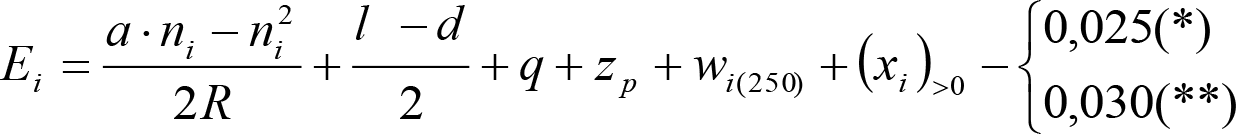
| (*) valor a aplicar en E i de partes bajas (h ≤ 0,400 m) | (**) valor a aplicar en E i de partes altas (h > 0,400 m) |
Según lo indicado en el apartado A.6.2.2, s=0. Por tanto zp=0.
El término (xi)>0, se calcula según lo indicado en el apartado A.6.2.3.1.
| Coche intermedio |
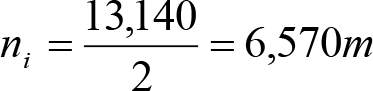
|
|||
| h (m) | zp(m) | Semiancho contorno de referencia (m) | Ei(m) | Semiancho disponible (m) |
| 4,330 | 0 | 0,800 | 0,142 | 0,658 |
| 4,100 | 0 | 1,250 | 0,142 | 1,108 |
| 3,700 | 0 | 1,580 | 0,142 | 1,438 |
| 3,320 | 0 | 1,720 | 0,142 | 1,578 |
| 1,150 | 0 | 1,720 | 0,142 | 1,578 |
| 1,150 | 0 | 1,695 | 0,142 | 1,553 |
| 0,600 | 0 | 1,695 | 0,142 | 1,553 |
| 0,600 | 0 | 1,675 | 0,142 | 1,533 |
| 0,400 | 0 | 1,675 | 0,142 | 1,533 |
| 0,400 | 0 | 1,637 | 0,142 | 1,495 |
|
Cuadro A.6.5. Resultados del cálculo del gálibo del material rodante GHE16 de un VCI con sistema pasivo. SITUACIÓN 2. Coche intermedio. |
||||
A continuación se incluyen tres ejemplos de aplicación de las fórmulas expuestas en el capítulo 3 para el cálculo del gálibo límite y uniforme de implantación de obstáculos, entreeje límite y gálibo del pantógrafo.
A.7.1 GÁLIBO LÍMITE DE IMPLANTACIÓN DE OBSTÁCULOS
A.7.1.1 GÁLIBO LÍMITE GC
Se considera el gálibo de partes altas GC, en una sección de vía con las siguientes características:
∙ Radio en planta: R = 250 m
∙ Radio de acuerdo vertical: Rv = 2.000 m
∙ Peralte: D = 0,160 m
∙ Insuficiencia de peralte: I = 0,150 m
∙ Vía en balasto, en mal estado
Además, de los apartados 3.11.1.1. y 3.11.1.2, para ancho estándar europeo:
∙ L = 1,500 m
∙ l N = 1,435 m
∙ l = lmáx = 1,465 m
∙ D0 = I0 = 0,050 m
∙ hc0 = 0,500 m
∙ Para gálibo GC (cuadro 2.16 del apartado 2.8.2.4): s0=0,4
Del cuadro 3.8 del apartado 3.10.1.3:
∙ Tvia = 0,025 m
∙ Para las hipótesis anteriores (R=250 m; D=0,160 m; I=0,150 m), la velocidad máxima de circulación será:
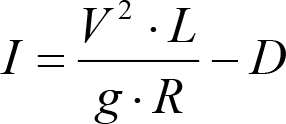
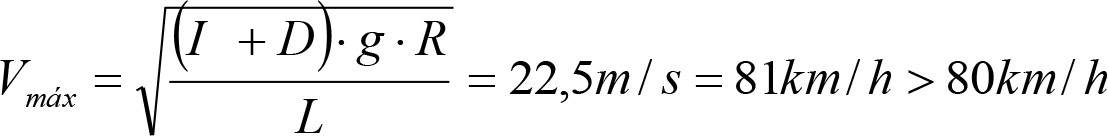 → TD =0,015 m.
→ TD =0,015 m.
∙ αc = 0,77º
∙ αsusp = 0,23º
∙ αosc para vía en mal estado:
− Desplazamientos laterales
∙ αosc = 0,2º (lado interior de la curva)
∙ αosc = 1º (lado exterior de la curva)
− Desplazamientos verticales
∙ αosc = 1º (lado interior de la curva)
∙ αosc = 0,2º (lado exterior de la curva
∙ TN = 0,020 m
∙ K = 1,2 excepto en el caso de los desplazamientos aleatorios laterales para h<0,5 m que se tomará un valor de K =1.
Las fórmulas a aplicar son las del gálibo límite de implantación de obstáculos, definidas en el apartado 3.3. Para las situaciones generalmente más desfavorables las fórmulas se definen en el apartado 3.11.2.
Se calculan los desplazamientos hacia el interior y exterior de la curva, en los siguientes casos:
a) Vehículo circulando a la máxima velocidad permitida (máxima insuficiencia de peralte I).
b) Vehículo parado (máximo exceso de peralte D).
Se han considerado los siguientes puntos del contorno de referencia (m):
| Punto | b | h | h-h co |
|---|---|---|---|
|
1 (PT) |
1,540 | 4,700 | 4,200 |
|
2 (Partes altas: puntos por encima de la anchura máxima) |
1,645 | 3,550 | 3,050 |
|
3 (Partes altas: puntos por debajo de la anchura máxima) |
1,645 | 1,170 | 0,670 |
|
4 (Partes bajas) |
1,620 | 0,400 | 0,000 |
Los salientes (m) serán:
| Punto | S i | S a |
|---|---|---|
| 1 | 0,030 | 0,030 |
| 2 | 0,030 | 0,030 |
| 3 | 0,030 | 0,030 |
| 4 | 0,025 | 0,025 |
Los desplazamientos cuasiestáticos laterales (mm) serán:
| Punto | V = V max | V = 0 | ||
|---|---|---|---|---|
| qs Ii | qs Ia | qs Di | qs Da | |
| 1 | 112,00 | 112,00 | 123,20 | 123,20 |
| 2 | 81,33 | 81,33 | 89,47 | 89,47 |
| 3 | 17,87 | 17,87 | 19,65 | 19,65 |
| 4 | 0,00 | 0,00 | 0,00 | 0,00 |
Los desplazamientos aleatorios laterales por desviaciones de peralte (mm) serán:
| Punto | Δb g | Δb c | Δb g + Δb c |
|---|---|---|---|
| 1 | 47,00 | 16,80 | 63,80 |
| 2 | 35,50 | 12,20 | 47,70 |
| 3 | 11,70 | 2,68 | 14,38 |
| 4 | 4,00 | 0,00 | 4,00 |
Los desplazamientos aleatorios laterales por disimetrías del vehículo (mm) serán:
| Punto | Δb susp | Δb carga | Δb ηo |
|---|---|---|---|
| 1 | 16,86 | 56,45 | 73,31 |
| 2 | 12,24 | 40,99 | 53,24 |
| 3 | 2,69 | 9,00 | 11,69 |
| 4 | 0,00 | 0,00 | 0,00 |
Los desplazamientos aleatorios laterales por oscilaciones del vehículo debidas a irregularidades de la vía (mm) serán:
| Punto | Interior | Exterior |
|---|---|---|
| Δb osc i | Δb osc a | |
| 1 | 14,66 | 73,31 |
| 2 | 10,65 | 53,24 |
| 3 | 2,34 | 11,69 |
| 4 | 0,00 | 0,00 |
La suma cuadrática de los desplazamientos aleatorios laterales será:
a) Para vehículo circulando a la máxima velocidad permitida (V = Vmax), con máxima insuficiencia de peralte I, hacia el interior y exterior de la curva:
| Punto | V =V max (I) | ||||
|---|---|---|---|---|---|
| ∑j 1 | ∑j 2 | ∑j* 1 | ∑j* 2 | ||
| Interior | 1i | 109,86 | -101,33 | ||
| 2i | 83,52 | -71,94 | |||
| 3i | 36,51 | 21,61 | |||
| 4i | 25,32 | 24,68 | |||
| Exterior | 1e | 139,64 | -133,04 | ||
| 2e | 104,37 | -95,36 | |||
| 3e | 39,01 | 16,68 | |||
| 4e | 25,32 | 24,68 | |||
b) Para vehículo parado (V = 0), con máximo exceso de peralte D, hacia el interior y exterior de la curva:
| Punto | V=0 (D) | ||||
|---|---|---|---|---|---|
| ∑j 1 | ∑j 2 | ∑j* 1 | ∑j* 2 | ||
| Interior | 1i | 109,86 | -101,33 | ||
| 2i | 83,52 | -71,94 | |||
| 3i | 36,51 | 21,61 | |||
| 4i | 25,32 | 24,68 | |||
| Exterior | 1e | 139,64 | -133,04 | ||
| 2e | 104,37 | -95,36 | |||
| 3e | 39,01 | 16,68 | |||
| 4e | 25,32 | 24,68 | |||
Los desplazamientos perpendiculares al plano de rodadura por inscripción en acuerdos verticales (mm) serán:
| Punto | Δh Rv |
|---|---|
| 1 | 25,00 |
| 2 | 25,00 |
| 3 | 25,00 |
| 4 | 25,00 |
Los desplazamientos cuasiestáticos perpendiculares al plano de rodadura (mm) serán:
| Punto | V = V max | V = 0 | ||
|---|---|---|---|---|
| Δh PTIi | Δh PTIa | Δh PTDi | Δh PTDa | |
| 1 | 41,07 | 41,07 | 45,17 | 45,17 |
| 2 | 0,00 | 0,00 | 0,00 | 0,00 |
| 3 | 0,00 | 0,00 | 0,00 | 0,00 |
| 4 | 0,00 | 0,00 | 0,00 | 0,00 |
Los desplazamientos aleatorios perpendiculares al plano de rodadura por desviaciones del peralte (mm) serán:
| Punto | Interior | Exterior |
|---|---|---|
| (Δh g + Δh c ) i | (Δh g + Δh c ) a | |
| 1 | 14,06 | 29,06 |
| 2 | 0,00 | 0,00 |
| 3 | 0,00 | 0,00 |
| 4 | 0,00 | 0,00 |
Los desplazamientos aleatorios perpendiculares al plano de rodadura por disimetrías del vehículo (mm) serán:
| Punto | Δh susp | Δh carga | Δh ηo |
|---|---|---|---|
| 1 | 6,18 | 20,70 | 26,88 |
| 2 | 0,00 | 0,00 | 0,00 |
| 3 | 0,00 | 0,00 | 0,00 |
| 4 | 0,00 | 0,00 | 0,00 |
Los desplazamientos aleatorios perpendiculares al plano de rodadura por oscilaciones del vehículo debidas a irregularidades de la vía (mm) serán:
| Punto | Interior | Exterior |
|---|---|---|
| Δh osc i | Δh osc a | |
| 1 | 26,88 | 5,38 |
| 2 | 0,00 | 0,00 |
| 3 | 0,00 | 0,00 |
| 4 | 0,00 | 0,00 |
La suma cuadrática de los desplazamientos aleatorios verticales será:
a) Para vehículo circulando a la máxima velocidad permitida (V = Vmax), con máxima insuficiencia de peralte I, hacia el interior y exterior de la curva:
| Punto | V =V max (I) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ∑V i1 | ∑V a1 | ∑V i2 | ∑V a2 | ∑V i1 * | ∑V a1 * | ∑V i2 * | ∑V a2 * | ||
| Interior | 1i | -33,71 | 50,73 | ||||||
| 2i | 20,00 | 20,00 | |||||||
| 3i | 20,00 | 20,00 | |||||||
| 4i | 20,00 | 20,00 | |||||||
| Exterior | 1e | -36,79 | 50,06 | ||||||
| 2e | 20,00 | 20,00 | |||||||
| 3e | 20,00 | 20,00 | |||||||
| 4e | 20,00 | 20,00 | |||||||
b) Para vehículo parado (V = 0), con máximo exceso de peralte D, hacia el interior y exterior de la curva:
| Punto | V=0 (D) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ∑V i1 | ∑V i2 | ∑V a2 | ∑V i1 * | ∑V a1 * | ∑V i2 * | ∑V a2 * | |||
| Interior | 1i | -33,71 | 50,73 | ||||||
| 2i | 20,00 | 20,00 | |||||||
| 3i | 20,00 | 20,00 | |||||||
| 4i | 20,00 | 20,00 | |||||||
| Exterior | 1e | -36,79 | 50,06 | ||||||
| 2e | 20,00 | 20,00 | |||||||
| 3e | 20,00 | 20,00 | |||||||
| 4e | 20,00 | 20,00 | |||||||
Finalmente, aplicando las fórmulas correspondientes a cada punto, se obtienen las siguientes combinaciones de movimientos (mm):
a) Para vehículo circulando a la máxima velocidad permitida (V = Vmax), con máxima insuficiencia de peralte I, hacia el interior y exterior de la curva:
| Punto | Gálibo límite (V = V max) | ||||
|---|---|---|---|---|---|
| bobstáculo máximo con h obstáculo compatible | hobstáculo máximo con b obstáculo compatible | ||||
| b | h | b | h | ||
| Interior | 4i | -1670,32 | 355,00 | -1669,68 | 355,00 |
| 3i | -1693,64 | 1125,00 | -1678,75 | 1125,00 | |
| 2i | -1677,18 | 3595,00 | -1521,73 | 3595,00 | |
| 1i | -1567,86 | 4732,36 | -1356,67 | 4816,79 | |
| Exterior | 1e | 1821,64 | 4647,14 | 1548,96 | 4733,99 |
| 2e | 1860,70 | 3595,00 | 1660,97 | 3595,00 | |
| 3e | 1731,88 | 1125,00 | 1709,54 | 1125,00 | |
| 4e | 1670,32 | 355,00 | 1669,68 | 355,00 | |
|
Cuadro A.7.1. Gálibo límite. Vehículo circulando a Vmáx (I) |
|||||
b) Para vehículo parado (V = 0), con máximo exceso de peralte D, hacia el interior y exterior de la curva:
| Punto | Gálibo límite (V = 0) | ||||
|---|---|---|---|---|---|
| bobstáculo máximo con h obstáculo compatible | hobstáculo máximo con b obstáculo compatible | ||||
| b | h | b | h | ||
| Interior | 4i | -1670,32 | 355,00 | -1669,68 | 355,00 |
| 3i | -1731,16 | 1125,00 | -1716,27 | 1125,00 | |
| 2i | -1847,98 | 3595,00 | -1692,53 | 3595,00 | |
| 1i | -1803,06 | 4646,12 | -1591,87 | 4730,55 | |
| Exterior | 1e | 1586,44 | 4733,38 | 1313,76 | 4820,23 |
| 2e | 1689,90 | 3595,00 | 1490,17 | 3595,00 | |
| 3e | 1694,36 | 1125,00 | 1672,02 | 1125,00 | |
| 4e | 1670,32 | 355,00 | 1669,68 | 355,00 | |
|
Cuadro A.7.2. Gálibo límite. Vehículo parado (D) |
|||||
El contorno de gálibo límite se obtiene dibujando los 4 contornos definidos anteriormente y hallando la envolvente de los mismos, tal y como se indica en la figura A.7.1. Los ejes X y Y, son respectivamente, paralelo y perpendicular al plano de rodadura.
|
Figura A7.1. Gálibo límite GC |
A.7.1.2 GÁLIBO LÍMITE GED10
Se considera el gálibo de partes altas GED10, en una sección de vía con las siguientes características:
∙ Radio en planta: R = 100 m
∙ Radio de acuerdo vertical: Rv = 2000 m
∙ Peralte: D = 0,110 m
∙ Insuficiencia de peralte: I = 0,070 m
∙ Vía en balasto, en mal estado
Además, de los apartados 3.12.1.1. y 3.12.1.2, para ancho métrico:
∙ L = 1,055 m
∙ l N = 1,000 m
∙ l = lmáx = 1,030 m
∙ D0= I0 = 0,070 m
∙ hc0 = 0,500 m
∙ s0 = 0,4 (del apartado 2.9.2.3)
Del cuadro 3.25 del apartado 3.12.1.3:
∙ Tvia = 0,025 m
∙ TD = 0,02 m.
∙ αc = 0,77º
∙ αsusp = 0,23º
∙ αosc
– Desplazamientos laterales
∙ αosc = 0,2º (lado interior de la curva)
∙ αosc = 1º (lado exterior de la curva)
– Desplazamientos verticales
∙ αosc = 1º (lado interior de la curva)
∙ αosc = 0,2º (lado exterior de la curva
∙ TN = 0,020 m
∙ K = 1,2 excepto en el caso de los desplazamientos aleatorios laterales para h<0,5 m que se tomará un valor de K =1.
Las fórmulas a aplicar son las del gálibo límite de implantación de obstáculos, definidas en el apartado 3.3. Para las situaciones generalmente más desfavorables las fórmulas se definen en el apartado 3.12.2.
Se calculan los desplazamientos hacia el interior y exterior de la curva, en los siguientes casos:
a) Vehículo circulando a la máxima velocidad permitida (máxima insuficiencia de peralte I).
b) Vehículo parado (máximo exceso de peralte D).
Se han considerado los siguientes puntos del contorno de referencia (m):
|
Punto |
b | h | h-h co |
|---|---|---|---|
|
1 (PT) |
0,750 | 3,900 | 3,400 |
|
2 (Partes altas: puntos por encima de la anchura máxima) |
1,150 | 3,800 | 3,300 |
|
3 (Partes altas: puntos por encima de la anchura máxima) |
1,530 | 3,550 | 3,050 |
|
4 (Partes bajas) |
1,530 | 0,400 | 0,000 |
Los salientes (m) serán:
| Punto | S i | S a |
|---|---|---|
| 1 | 0,030 | 0,030 |
| 2 | 0,030 | 0,030 |
| 3 | 0,030 | 0,030 |
| 4 | 0,025 | 0,025 |
Los desplazamientos cuasiestáticos laterales (mm) serán:
| Punto | V = V max | V = 0 | ||
|---|---|---|---|---|
| qs Ii | qs Ia | qs Di | qs Da | |
| 1 | 0,00 | 0,00 | 51,56 | 51,56 |
| 2 | 0,00 | 0,00 | 50,05 | 50,05 |
| 3 | 0,00 | 0,00 | 46,26 | 46,26 |
| 4 | 0,00 | 0,00 | 0,00 | 0,00 |
Los desplazamientos aleatorios laterales por desviaciones de peralte (mm) serán:
| Punto | Δb g | Δb c | Δb g + Δb c |
|---|---|---|---|
| 1 | 73,93 | 25,78 | 99,72 |
| 2 | 72,04 | 25,02 | 97,06 |
| 3 | 67,30 | 23,13 | 90,43 |
| 4 | 7,58 | 0,00 | 7,58 |
Los desplazamientos aleatorios laterales por disimetrías del vehículo (mm) serán:
| Punto | Δb susp | Δb carga | Δb ηo |
|---|---|---|---|
| 1 | 13,65 | 45,70 | 59,35 |
| 2 | 13,25 | 44,35 | 57,60 |
| 3 | 12,24 | 40,99 | 53,24 |
| 4 | 0,00 | 0,00 | 0,00 |
Los desplazamientos aleatorios laterales por oscilaciones del vehículo debidas a irregularidades de la vía (mm) serán:
| Punto | Interior | Exterior |
|---|---|---|
| Δb osc i | Δb osc a | |
| 1 | 11,87 | 59,35 |
| 2 | 11,52 | 57,60 |
| 3 | 10,65 | 53,24 |
| 4 | 0,00 | 0,00 |
La suma cuadrática de los desplazamientos aleatorios laterales será:
a) Para vehículo circulando a la máxima velocidad permitida (V = Vmax), con máxima insuficiencia de peralte I, hacia el interior y exterior de la curva:
| Punto | V =V max (I) | ||||
|---|---|---|---|---|---|
| ∑j 1 | ∑j 2 | ∑j 1 * | ∑j 2 * | ||
| Interior | 1i | 136,73 | -129,99 | ||
| 2i | 133,20 | -126,26 | |||
| 3i | 124,39 | -116,93 | |||
|
4i |
26,12 |
--- |
23,82 |
||
| Exterior | 1e | 153,51 | -147,53 | ||
| 2e | 149,43 | -143,28 | |||
| 3e | 139,25 | -132,63 | |||
|
4e |
26,12 |
23,82 |
|||
b) Para vehículo parado (V = 0), con máximo exceso de peralte D, hacia el interior y exterior de la curva:
| Punto | V=0 (D) | ||||
|---|---|---|---|---|---|
| ∑j 1 | ∑j 2 | ∑j 1 * | ∑j 2 * | ||
| Interior | 1i | 136,73 | -129,99 | ||
| 2i | 133,20 | -126,26 | |||
| 3i | 124,39 | -116,93 | |||
|
4i |
26,12 |
23,82 |
|||
| Exterior | 1e | 153,51 | -147,53 | ||
| 2e | 149,43 | -143,28 | |||
| 3e | 139,25 | -132,63 | |||
|
4e |
26,12 |
23,82 |
|||
Los desplazamientos perpendiculares al plano de rodadura por inscripción en acuerdos verticales (mm) serán:
| Punto | Δh Rv |
|---|---|
| 1 | 25,00 |
| 2 | 25,00 |
| 3 | 25,00 |
| 4 | 25,00 |
Los desplazamientos cuasiestáticos perpendiculares al plano de rodadura (mm) serán:
| Punto | V = V max | V = 0 | ||
|---|---|---|---|---|
| Δh PTIi | Δh PTIa | Δh PTDi | Δh PTDa | |
| 1 | 0,00 | 0,00 | 11,37 | 11,37 |
| 2 | 0,00 | 0,00 | 0,00 | 0,00 |
| 3 | 0,00 | 0,00 | 0,00 | 0,00 |
| 4 | 0,00 | 0,00 | 0,00 | 0,00 |
Los desplazamientos aleatorios perpendiculares al plano de rodadura por desviaciones del peralte (mm) serán:
| Punto | Interior | Exterior |
|---|---|---|
| (Δh g + Δh c ) i | (Δh g + Δh c ) a | |
| 1 | 9,91 | 29,91 |
| 2 | 0,00 | 0,00 |
| 3 | 0,00 | 0,00 |
| 4 | 0,00 | 0,00 |
Los desplazamientos aleatorios perpendiculares al plano de rodadura por disimetrías del vehículo (mm) serán:
| Punto | Δh susp | Δh carga | Δh ηo |
|---|---|---|---|
| 1 | 3,01 | 10,08 | 13,09 |
| 2 | 0,00 | 0,00 | 0,00 |
| 3 | 0,00 | 0,00 | 0,00 |
| 4 | 0,00 | 0,00 | 0,00 |
Los desplazamientos aleatorios perpendiculares al plano de rodadura por oscilaciones del vehículo debidas a irregularidades de la vía (mm) serán:
| Punto | Interior | Exterior |
|---|---|---|
| Δh osc i | Δh osc a | |
| 1 | 13,09 | 2,62 |
| 2 | 0,00 | 0,00 |
| 3 | 0,00 | 0,00 |
| 4 | 0,00 | 0,00 |
La suma cuadrática de los desplazamientos aleatorios verticales será:
a) Para vehículo circulando a la máxima velocidad permitida (V = Vmax), con máxima insuficiencia de peralte I, hacia el interior y exterior de la curva:
| Punto | V =V max (I) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ∑V i1 | ∑V a1 | ∑V i2 | ∑V a2 | ∑V i1 * | ∑V a1 * | ∑V i2 * | ∑V a2 * | ||
| Interior |
1i |
13,03 |
|
|
|
33,52 |
|
|
|
|
2i |
|
|
20,00 |
|
|
|
20,00 |
|
|
|
3i |
|
|
20,00 |
|
|
|
20,00 |
|
|
|
4i |
|
|
20,00 |
|
|
|
20,00 |
|
|
| Exterior |
1e |
|
-29,68 |
|
|
|
45,09 |
|
|
|
2e |
|
|
|
20,00 |
|
|
|
20,00 |
|
|
3e |
|
|
|
20,00 |
|
|
|
20,00 |
|
|
4e |
|
|
|
20,00 |
|
|
|
20,00 |
|
Para vehículo parado (V = 0), con máximo exceso de peralte D, hacia el interior y exterior de la curva:
| Punto | V=0 (D) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ∑V i1 | ∑V a1 | ∑V i2 | ∑V a2 | ∑V i1 * | ∑V a1 * | ∑V i2 * | ∑V a2 * | ||
| Interior | 1i | 13,03 | 33,52 | ||||||
| 2i | 20,00 | 20,00 | |||||||
| 3i | 20,00 | 20,00 | |||||||
|
4i |
20,00 |
20,00 |
|||||||
| Exterior | 1e | -29,68 | 45,09 | ||||||
| 2e | 20,00 | 20,00 | |||||||
| 3e | 20,00 | 20,00 | |||||||
|
4e |
20,00 |
20,00 |
|||||||
Finalmente, aplicando las fórmulas correspondientes a cada punto, se obtienen las siguientes combinaciones de movimientos (mm):
a) Para vehículo circulando a la máxima velocidad permitida (V = Vmax), con máxima insuficiencia de peralte I, hacia el interior y exterior de la curva:
| Punto | Gálibo límite (V = V max) | ||||
|---|---|---|---|---|---|
| bobstáculo máximo con h obstáculo compatible | hobstáculo máximo con b obstáculo compatible | ||||
| b | h | b | h | ||
| Interior |
4i |
-1581,12 |
355,00 |
-1578,82 |
355,00 |
| 3i | -1684,39 | 3595,00 | -1443,07 | 3595,00 | |
| 2i | -1351,73 | 3845,00 | -1085,01 | 3845,00 | |
| 1i | -673,81 | 3938,03 | -392,59 | 3958,52 | |
| Exterior | 1e | 691,68 | 3895,32 | 373,98 | 3970,09 |
| 2e | 1368,51 | 3845,00 | 1067,47 | 3845,00 | |
| 3e | 1699,25 | 3595,00 | 1427,37 | 3595,00 | |
|
4e |
1581,12 |
355,00 |
1578,82 |
355,00 |
|
|
Cuadro A.7.3. Gálibo límite. Vehículo circulando a Vmáx (I) |
|||||
b) Para vehículo parado (V = 0), con máximo exceso de peralte D, hacia el interior y exterior de la curva:
| Punto | Gálibo límite (V = 0) | ||||
|---|---|---|---|---|---|
| bobstáculo máximo con h obstáculo compatible | hobstáculo máximo con b obstáculo compatible | ||||
| b | h | b | h | ||
| Interior |
4i |
-1581,12 |
355,00 |
-1578,82 |
355,00 |
| 3i | -1730,65 | 3595,00 | -1489,32 | 3595,00 | |
| 2i | -1403,30 | 3845,00 | -1136,58 | 3845,00 | |
| 1i | -728,41 | 3926,66 | -447,18 | 3947,14 | |
| Exterior | 1e | 637,08 | 3906,69 | 319,39 | 3981,46 |
| 2e | 1316,95 | 3845,00 | 1015,91 | 3845,00 | |
| 3e | 1653,00 | 3595,00 | 1381,11 | 3595,00 | |
|
4e |
1581,12 |
355,00 |
1578,82 |
355,00 |
|
|
Cuadro A.7.4. Gálibo límite. Vehículo parado (D) |
|||||
El contorno de gálibo límite se obtiene dibujando los 4 contornos definidos anteriormente y hallando la envolvente de los mismos.
A.7.2 GÁLIBO MECÁNICO Y ELÉCTRICO DEL PANTÓGRAFO
Se consideran los siguientes datos:
∙ Gálibo GC en línea nueva.
∙ Catenaria EAC-350: 25 kV corriente alterna
∙ Ancho del pantógrafo: 1.950 mm. → Del cuadro 3.5 se obtiene: bw = 975 mm
∙ hf = 5300 mm
∙ Radio en planta: R = 250 m
∙ Peralte: D = 0,160 m
∙ Insuficiencia de peralte: I = 0,150 m
∙ l = 1,465 m
∙ Vía en mal estado
Del apartado 3.11.4.2:
∙ epo = 0,170 m, a la máxima altura de verificación h’0 = 6,5 m
∙ epu = 0,110 m, a la mínima altura de verificación h’u = 5 m
∙ L = 1,500 m
∙ s’0 = 0,225
∙ h’c0 = 0,5 m
∙ D’o=I’o=1/15 ≈ 0,066m
∙ cw = 0
Del cuadro 3.7 del apartado 3.5.2:
∙ belec (estática) = 270 mm
∙ belec (dinámica) = 150 mm
Del cuadro 3.8 del apartado 3.10.1.3:
∙ Tvía=0,025 m
∙ Para las hipótesis anteriores (R=250 m; D=0,160 m; I=0,150 m), la velocidad máxima de circulación será:
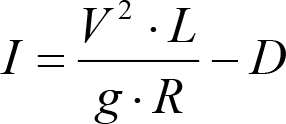
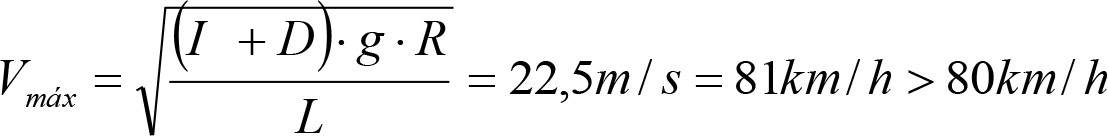 → TD =0,015 m.
→ TD =0,015 m.
∙ αc = 0,77º
∙ αsusp = 0,23º
∙ K’ = 1
Para vía en mal estado del apartado 3.11.4.2:
– αosc = 0,11º (lado interior de la curva)
– αosc = 0,6º (lado exterior de la curva)
Del cuadro 3.4 del apartado 3.5.1.3 para catenaria EAC-350:
∙ fs = 162 mm (con V= Vmáx)
∙ fs = 41 mm (con V=0)
∙ fws+fwa = 70 mm
Las fórmulas a aplicar son las definidas en el apartado 3.11.4.
Se calculan los desplazamientos hacia el interior y exterior de la curva, en los siguientes casos:
a) Vehículo circulando a la máxima velocidad permitida (máxima insuficiencia de peralte I).
b) Vehículo parado (máximo exceso de peralte D).
Se han considerado los siguientes puntos del contorno de referencia (m):
|
Punto |
h | h-h co |
|---|---|---|
| 1 | 5,000 | 4,500 |
| 2 | 6,500 | 6,000 |
Los salientes (m) serán los definidos en el apartado 3.11.4.2:
| Punto | S’ i | S’ a |
|---|---|---|
| 1 | 0,025 | 0,025 |
| 2 | 0,025 | 0,025 |
Los desplazamientos cuasiestáticos laterales (mm) serán:
| Punto | V = V max | V = 0 |
|---|---|---|
| qs’ a |
qs’ i |
|
| 1 | 56,70 |
63,45 |
| 2 | 75,60 |
84,60 |
Los desplazamientos aleatorios laterales por desviaciones de peralte (mm) serán:
| Punto | Δb g | Δb c | Δb g + Δb c |
|---|---|---|---|
| 1 | 50,00 | 10,13 | 60,13 |
| 2 | 65,00 | 13,50 | 78,50 |
Los desplazamientos aleatorios laterales por disimetrías del vehículo (mm) serán:
| Punto | Δb susp | Δb carga | Δb ηo |
|---|---|---|---|
| 1 | 18,06 | 60,48 | 78,54 |
| 2 | 24,09 | 80,64 | 104,73 |
Los desplazamientos aleatorios laterales por oscilaciones del vehículo debidas a irregularidades de la vía (mm) serán:
| Punto | Interior | Exterior |
|---|---|---|
| Δb osc i | Δb osc a | |
| 1 | 8,64 | 47,13 |
| 2 | 11,52 | 62,83 |
La suma cuadrática de los desplazamientos aleatorios laterales será:
a) Para vehículo circulando a la máxima velocidad permitida (V = Vmax), con máxima insuficiencia de peralte I, hacia el interior y exterior de la curva:
| Punto | V =V max (I) | |
|---|---|---|
| ∑j’ | ||
| Interior | 1i | 91,10 |
| 2i | 118,33 | |
| Exterior | 1e | 102,20 |
| 2e | 133,48 | |
b) Para vehículo parado (V = 0), con máximo exceso de peralte D, hacia el interior y exterior de la curva:
| Punto | V=0 (D) | |
|---|---|---|
| ∑j’ | ||
| Interior | 1i | 91,10 |
| 2i | 118,33 | |
| Exterior | 1e | 102,20 |
| 2e | 133,48 | |
a) Anchura del gálibo mecánico (en mm)
| Punto | b w | e p | S’ i = S’ a | qs’ i / qs’ a | ∑j’ | b obstáculo,i / b obstáculo,a | |
|---|---|---|---|---|---|---|---|
| Interior | 1i | 975 | 110 | 25 | 63,45 | 91,10 | 1264,55 |
| 2i | 975 | 170 | 25 | 84,60 | 118,33 | 1372,93 | |
| Exterior | 1e | 975 | 110 | 25 | 56,70 | 102,20 | 1268,90 |
| 2e | 975 | 170 | 25 | 75,60 | 133,48 | 1379,08 | |
b) Altura del gálibo mecánico (en mm)
Para vehículo circulando a la máxima velocidad permitida (V = Vmax)
heff= hf+ fs + fws+fwa = 5,3 + 0,162 + 0,070 = 5,532 m
Para vehículo parado (V = 0)
heff= hf+ fs + fws+fwa = 5,3 + 0,041 + 0,070 = 5,411 m
c) Anchura del gálibo eléctrico (en mm)
| Punto | b obstáculo,i /b obstáculo,a | b elec | c w | b obstáculo,i,elec /b obstáculo,a,elec | |
|---|---|---|---|---|---|
| Interior | 1i | 1264,55 | 270 | 0 | 1534,55 |
| 2i | 1372,93 | 270 | 0 | 1642,93 | |
| Exterior | 1e | 1268,90 | 150 | 0 | 1418,90 |
| 2e | 1379,08 | 150 | 0 | 1529,08 | |
d) Altura del gálibo eléctrico (en mm)
Para vehículo circulando a la máxima velocidad permitida (V = Vmax)
heff,elec = heff +belec= 5,532+0,150 = 5,682 m
Para vehículo parado (V = 0)
heff,elec = heff +belec= 5,411+0,270 = 5,681 m
En la figura A7.2 se define el gálibo eléctrico y mecánico del pantógrafo. Los ejes X y Y, son respectivamente, paralelo y perpendicular al plano de rodadura.
|
* Geometría en función del tipo de pantógrafo utilizado Figura A.7.2. Gálibo mecánico y eléctrico del pantógrafo |
A.7.3 GÁLIBO UNIFORME DE IMPLANTACIÓN DE OBSTÁCULOS
A.7.3.1 GÁLIBO NOMINAL GC
Se considera el gálibo de partes altas GC, con las hipótesis establecidas en el apartado 3.11.7:
∙ Radio mínimo en planta: R = 250 m
∙ Radio mínimo de acuerdo vertical: Rv = 2.000 m
∙ Sobreancho máximo: 30 mm
∙ Peralte máximo: D = 0,160 m
∙ Insuficiencia de peralte máxima: Imax = 0,150 m
∙ Vía en balasto, en mal estado
∙ Catenaria EAC-350.
∙ Pantógrafo con ancho de la mesilla 2xbw=1.950 mm y trocadores no aislados cw=0
Además, de los apartados 3.11.1.1. y 3.11.1.2, para ancho estándar europeo:
∙ L = 1,500 m
∙ l N = 1,435 m
∙ l = lmáx = 1,465 m
∙ D0 = I0 = 0,050 m
∙ hc0 = 0,5 m
∙ Para gálibo GC (cuadro 2.16 del apartado 2.8.2.4): s0=0,4
Del cuadro 3.8 del apartado 3.10.1.3:
∙ Tvia = 0,025 m
∙ Para las hipótesis anteriores (R=250 m; D=0,160 m; Imax=0,150 m), la velocidad máxima de circulación será:
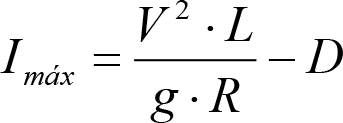
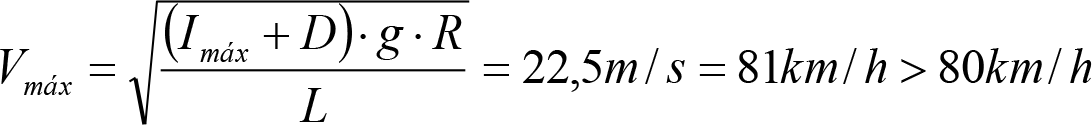 → TD =0,015 m.
→ TD =0,015 m.
∙ αc = 0,77º
∙ αsusp = 0,23º
∙ αosc para vía en mal estado:
– Desplazamientos laterales
∙ αosc = 0,2º (lado interior de la curva)
∙ αosc = 1º (lado exterior de la curva)
– Desplazamientos verticales
∙ αosc = 1º (lado interior de la curva)
∙ αosc = 0,2º (lado exterior de la curva
∙ TN = 0,020 m
Además, del apartado 3.11.1.4:
∙ Márgenes complementarios laterales: M3b = 0,200 m
∙ Márgenes complementarios perpendiculares al plano de rodadura: M3h = 0,150 m
Las fórmulas a aplicar son las del gálibo nominal de implantación de obstáculos, definidas en el apartado 3.4. Para las situaciones generalmente más desfavorables las fórmulas se definen en el apartado 3.11.3.
Se calculan los desplazamientos hacia el interior y exterior de la curva, en los siguientes casos:
a) Vehículo circulando a la máxima velocidad permitida (máxima insuficiencia de peralte I).
b) Vehículo parado (máximo exceso de peralte D).
La suma aritmética de los desplazamientos aleatorios laterales será:
a) Para vehículo circulando a la máxima velocidad permitida (V = Vmax), con máxima insuficiencia de peralte I, hacia el interior y exterior de la curva:
| Punto | V =V max (I) | ||||
|---|---|---|---|---|---|
| ∑j 3 | ∑j 4 | ∑j* 3 | ∑j* 4 | ||
| Interior | 1i | 176,77 | -126,77 | ||
| 2i | 136,58 | -86,58 | |||
| 3i | 53,41 | -3,41 | |||
| 4i | 29,00 | 21,00 | |||
| Exterior | 1e | 235,42 | -185,42 | ||
| 2e | 179,18 | -129,18 | |||
| 3e | 62,77 | -12,77 | |||
| 4e | 29,00 | 21,00 | |||
b) Para vehículo parado (V = 0), con máximo exceso de peralte D, hacia el interior y exterior de la curva:
| Punto | V=0 (D) | ||||
|---|---|---|---|---|---|
| ∑j 3 | ∑j 4 | ∑j* 3 | ∑j* 4 | ||
| Interior | 1i | 176,77 | -126,77 | ||
| 2i | 136,58 | -86,58 | |||
| 3i | 53,41 | -3,41 | |||
| 4i | 29,00 | 21,00 | |||
| Exterior | 1e | 235,42 | -185,42 | ||
| 2e | 179,18 | -129,18 | |||
| 3e | 62,77 | -12,77 | |||
| 4e | 29,00 | 21,00 | |||
La suma aritmética de los desplazamientos aleatorios verticales será:
a) Para vehículo circulando a la máxima velocidad permitida (V = Vmax), con máxima insuficiencia de peralte I, hacia el interior y exterior de la curva:
| Punto | V =V max (I) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ∑V i3 | ∑V a3 | ∑V i4 | ∑V a4 | ∑V i3 * | ∑V a3 * | ∑V i4 * | ∑V a4 * | ||
| Interior | 1i | -33,76 | 87,82 | ||||||
| 2i | 20,00 | 20,00 | |||||||
| 3i | 20,00 | 20,00 | |||||||
| 4i | 20,00 | 20,00 | |||||||
| Exterior | 1e | -41,32 | 81,32 | ||||||
| 2e | 20,00 | 20,00 | |||||||
| 3e | 20,00 | 20,00 | |||||||
| 4e | 20,00 | 20,00 | |||||||
b) Para vehículo parado (V = 0), con máximo exceso de peralte D, hacia el interior y exterior de la curva:
| Punto | V=0 (D) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| ∑V i3 | ∑V a3 | ∑V i4 | ∑V a4 | ∑V i3 * | ∑V a3 * | ∑V i4 * | ∑V a4 * | ||
| Interior | 1i | -33,76 | 87,82 | ||||||
| 2i | 20,00 | 20,00 | |||||||
| 3i | 20,00 | 20,00 | |||||||
| 4i | 20,00 | 20,00 | |||||||
| Exterior | 1e | -41,32 | 81,32 | ||||||
| 2e | 20,00 | 20,00 | |||||||
| 3e | 20,00 | 20,00 | |||||||
| 4e | 20,00 | 20,00 | |||||||
Finalmente, aplicando las fórmulas correspondientes a cada punto, se obtienen las siguientes combinaciones de movimientos (mm):
a) Para vehículo circulando a la máxima velocidad permitida (V=Vmax), con máxima insuficiencia de peralte I, hacia el interior y exterior de la curva:
| Punto | Gálibo nominal (V = V max) | ||||
|---|---|---|---|---|---|
| bobstáculo máximo con h obstáculo compatible | hobstáculo máximo con b obstáculo compatible | ||||
| b | h | b | h | ||
| Interior | 4i | -1874,00 | 205,00 | -1866,00 | 205,00 |
| 3i | -1910,55 | 975,00 | -1853,72 | 975,00 | |
| 2i | -1930,25 | 3745,00 | -1707,08 | 3745,00 | |
| 1i | -1834,77 | 4882,31 | -1531,23 | 5003,89 | |
| Exterior | 1e | 2117,42 | 4792,62 | 1696,58 | 4915,25 |
| 2e | 2135,51 | 3745,00 | 1827,16 | 3745,00 | |
| 3e | 1955,64 | 975,00 | 1880,10 | 975,00 | |
| 4e | 1874,00 | 205,00 | 1866,00 | 205,00 | |
|
Cuadro A.7.5. Gálibo nominal. Vehículo circulando a Vmáx (I) |
|||||
b) Para vehículo parado (V = 0), con máximo exceso de peralte D, hacia el interior y exterior de la curva:
| Punto | Gálibo nominal (V = 0) | ||||
|---|---|---|---|---|---|
| bobstáculo máximo con h obstáculo compatible | hobstáculo máximo con b obstáculo compatible | ||||
| b | h | b | h | ||
| Interior | 4i | -1874,00 | 205,00 | -1866,00 | 205,00 |
| 3i | -1948,07 | 975,00 | -1891,24 | 975,00 | |
| 2i | -2101,05 | 3745,00 | -1877,88 | 3745,00 | |
| 1i | -2069,97 | 4796,07 | -1766,43 | 4917,65 | |
| Exterior | 1e | 1882,22 | 4878,86 | 1461,38 | 5001,49 |
| 2e | 1964,71 | 3745,00 | 1656,36 | 3745,00 | |
| 3e | 1918,12 | 975,00 | 1842,58 | 975,00 | |
| 4e | 1874,00 | 205,00 | 1866,00 | 205,00 | |
|
Cuadro A.7.6. Gálibo nominal. Vehículo parado (D) |
|||||
El contorno de gálibo nominal se obtiene dibujando los 4 contornos definidos anteriormente y hallando la envolvente simétrica de los mismos, tal y como se indica en la siguiente figura. Los ejes X y Y, son respectivamente, paralelo y perpendicular al plano de rodadura.
|
Figura A.7.3. Gálibo nominal GC |
A.7.3.2 GÁLIBO UNIFORME GC
A continuación, se procede a homogeneizar la figura, rectificar los laterales de la misma, añadir el gálibo para partes bajas y el gálibo envolvente para el pantógrafo, y los huecos para los andenes y aceras de evacuación en túneles (comprobando que éstos últimos no sobrepasen el gálibo nominal dibujado).
De esta forma queda definido el gálibo uniforme en la figura A7.4. Los ejes X y Y, son respectivamente, paralelo y perpendicular al plano de rodadura.
|
Figura A.7.4. Gálibo uniforme GC
|
A.7.4 ENTREEJE LÍMITE
Se consideran dos vías paralelas de gálibo GEC16 (so = 0,4), situadas en curva, con las siguientes características:
|
Vía 1 (curva exterior) |
Vía 2 (curva interior) |
|
|---|---|---|
| R | 450 m | 450 m |
| D | 0,120 m | 0,090 m |
| l=l max | 1,698 m | 1,698 m |
| I | 0,099 | 0,105 |
| Vías en mal estado | ||
Se considera el siguiente punto del contorno de referencia:
∙ hP = 3,320 m
∙ bCR = 1,720 m
El mayor entreeje se da con un vehículo parado en la vía exterior (de mayor peralte) y otro circulando en la vía interior (de menor peralte).
Las fórmulas a aplicar son las definidas en el apartado 3.10.5.1:
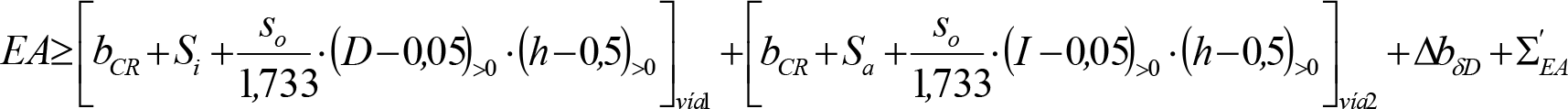
siendo:
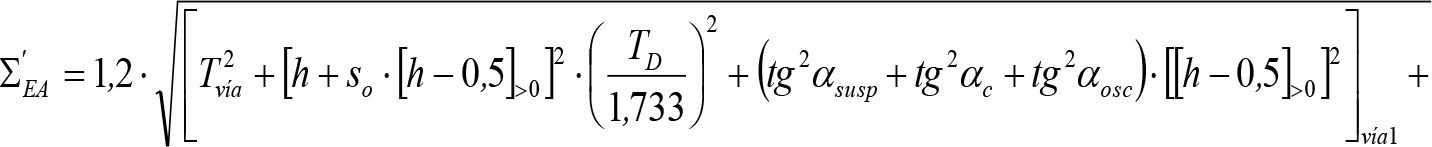

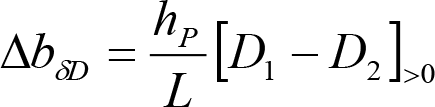 (definido en 3.6.1).
(definido en 3.6.1).
Del cuadro 3.8 del apartado. 3.10.1.3:
∙ Tvía 1 = Tvía 2 = 0,025 m
∙ Para las características de las vías indicadas, las velocidades máximas de circulación en cada vía serán:
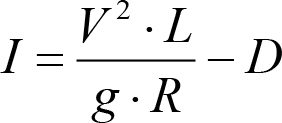
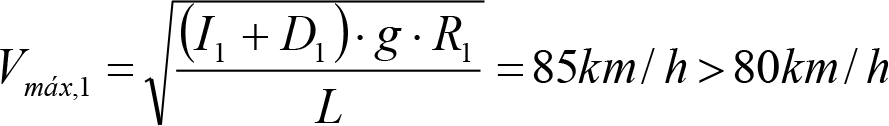 TD1 = 0,015 m
TD1 = 0,015 m
 TD2 = 0,015 m
TD2 = 0,015 m
∙ αc = 0,77º (en ambas vías)
∙ αsusp = 0,23º (en ambas vías)
∙ Para vías en mal estado:
∙ αosc = 0,2º (lado interior de la curva en vía 1).
∙ αosc= 1º (lado exterior de la curva en vía 2).
Los salientes serán los indicados en el cuadro 2.7 del apartado 2.7.2.4:
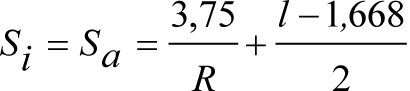
| b CR | S i = S a | qs i = qs a | |
|---|---|---|---|
| Vía 1 | 1,720 | 0,023 | 0,046 |
| Vía 2 | 1,720 | 0,023 | 0,036 |
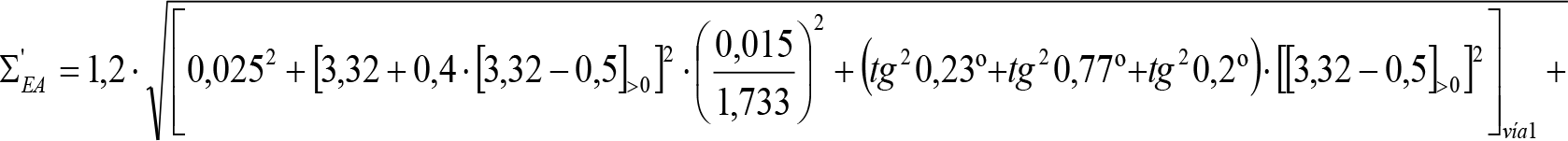
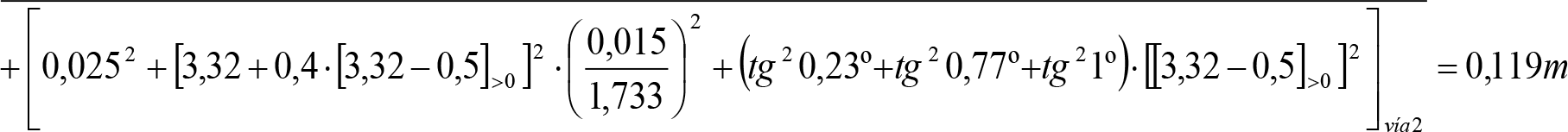

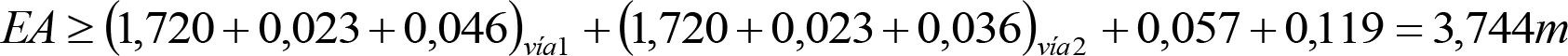
A.8.1 GÁLIBO GHE16
| Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 430 | 1650 | |||||||||
| 3290 | 1650 | |||||||||
| 3300 | 1646 | 3600 | 1532 | 3900 | 1312 | 4200 | 913 | |||
| 3310 | 1642 | 3610 | 1528 | 3910 | 1304 | 4210 | 893 | |||
| 3320 | 1638 | 3620 | 1524 | 3920 | 1296 | 4220 | 873 | |||
| 3330 | 1635 | 3630 | 1520 | 3930 | 1287 | 4230 | 853 | |||
| 3340 | 1631 | 3640 | 1516 | 3940 | 1279 | 4240 | 834 | |||
| 3350 | 1627 | 3650 | 1513 | 3950 | 1270 | 4250 | 814 | |||
| 3360 | 1623 | 3660 | 1509 | 3960 | 1262 | 4260 | 794 | |||
| 3370 | 1619 | 3670 | 1505 | 3970 | 1254 | 4270 | 774 | |||
| 3380 | 1616 | 3680 | 1497 | 3980 | 1245 | 4280 | 755 | |||
| 3390 | 1612 | 3690 | 1488 | 3990 | 1237 | 4290 | 735 | |||
| 3400 | 1608 | 3700 | 1480 | 4000 | 1229 | 4300 | 715 | |||
| 3410 | 1604 | 3710 | 1471 | 4010 | 1220 | |||||
| 3420 | 1600 | 3720 | 1463 | 4020 | 1212 | |||||
| 3430 | 1597 | 3730 | 1455 | 4030 | 1203 | |||||
| 3440 | 1593 | 3740 | 1446 | 4040 | 1195 | |||||
| 3450 | 1589 | 3750 | 1438 | 4050 | 1187 | |||||
| 3460 | 1585 | 3760 | 1430 | 4060 | 1178 | |||||
| 3470 | 1581 | 3770 | 1421 | 4070 | 1170 | |||||
| 3480 | 1577 | 3780 | 1413 | 4080 | 1150 | |||||
| 3490 | 1574 | 3790 | 1404 | 4090 | 1130 | |||||
| 3500 | 1570 | 3800 | 1396 | 4100 | 1111 | |||||
| 3510 | 1566 | 3810 | 1388 | 4110 | 1091 | |||||
| 3520 | 1562 | 3820 | 1379 | 4120 | 1071 | |||||
| 3530 | 1558 | 3830 | 1371 | 4130 | 1051 | |||||
| 3540 | 1555 | 3840 | 1363 | 4140 | 1031 | |||||
| 3550 | 1551 | 3850 | 1354 | 4150 | 1012 | |||||
| 3560 | 1547 | 3860 | 1346 | 4160 | 992 | |||||
| 3570 | 1543 | 3870 | 1337 | 4170 | 972 | |||||
| 3580 | 1539 | 3880 | 1329 | 4180 | 952 | |||||
| 3590 | 1535 | 3890 | 1321 | 4190 | 933 | |||||
| 3600 | 1532 | 3900 | 1312 | 4200 | 913 |
A.8.2 GÁLIBO GEA16
| Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 430 | 1650 | |||||||||
| 3290 | 1650 | |||||||||
| 3300 | 1646 | 3600 | 1532 | 3900 | 1312 | 4200 | 913 | |||
| 3310 | 1642 | 3610 | 1528 | 3910 | 1304 | 4210 | 893 | |||
| 3320 | 1638 | 3620 | 1524 | 3920 | 1296 | 4220 | 873 | |||
| 3330 | 1635 | 3630 | 1520 | 3930 | 1287 | 4230 | 853 | |||
| 3340 | 1631 | 3640 | 1516 | 3940 | 1279 | 4240 | 834 | |||
| 3350 | 1627 | 3650 | 1513 | 3950 | 1270 | 4250 | 814 | |||
| 3360 | 1623 | 3660 | 1509 | 3960 | 1262 | 4260 | 794 | |||
| 3370 | 1619 | 3670 | 1505 | 3970 | 1254 | 4270 | 774 | |||
| 3380 | 1616 | 3680 | 1497 | 3980 | 1245 | 4280 | 755 | |||
| 3390 | 1612 | 3690 | 1488 | 3990 | 1237 | 4290 | 735 | |||
| 3400 | 1608 | 3700 | 1480 | 4000 | 1229 | 4300 | 715 | |||
| 3410 | 1604 | 3710 | 1471 | 4010 | 1220 | 4310 | 695 | |||
| 3420 | 1600 | 3720 | 1463 | 4020 | 1212 | 4320 | 675 | |||
| 3430 | 1597 | 3730 | 1455 | 4030 | 1203 | |||||
| 3440 | 1593 | 3740 | 1446 | 4040 | 1195 | |||||
| 3450 | 1589 | 3750 | 1438 | 4050 | 1187 | |||||
| 3460 | 1585 | 3760 | 1430 | 4060 | 1178 | |||||
| 3470 | 1581 | 3770 | 1421 | 4070 | 1170 | |||||
| 3480 | 1577 | 3780 | 1413 | 4080 | 1150 | |||||
| 3490 | 1574 | 3790 | 1404 | 4090 | 1130 | |||||
| 3500 | 1570 | 3800 | 1396 | 4100 | 1111 | |||||
| 3510 | 1566 | 3810 | 1388 | 4110 | 1091 | |||||
| 3520 | 1562 | 3820 | 1379 | 4120 | 1071 | |||||
| 3530 | 1558 | 3830 | 1371 | 4130 | 1051 | |||||
| 3540 | 1555 | 3840 | 1363 | 4140 | 1031 | |||||
| 3550 | 1551 | 3850 | 1354 | 4150 | 1012 | |||||
| 3560 | 1547 | 3860 | 1346 | 4160 | 992 | |||||
| 3570 | 1543 | 3870 | 1337 | 4170 | 972 | |||||
| 3580 | 1539 | 3880 | 1329 | 4180 | 952 | |||||
| 3590 | 1535 | 3890 | 1321 | 4190 | 933 | |||||
| 3600 | 1532 | 3900 | 1312 | 4200 | 913 |
A.8.3 GÁLIBO GEB16
| Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 430 | 1650 | |||||||||
| 3290 | 1650 | |||||||||
| 3300 | 1646 | 3600 | 1532 | 3900 | 1375 | 4200 | 965 | |||
| 3310 | 1642 | 3610 | 1528 | 3910 | 1370 | 4210 | 941 | |||
| 3320 | 1638 | 3620 | 1524 | 3920 | 1364 | 4220 | 917 | |||
| 3330 | 1635 | 3630 | 1520 | 3930 | 1358 | 4230 | 892 | |||
| 3340 | 1631 | 3640 | 1516 | 3940 | 1353 | 4240 | 868 | |||
| 3350 | 1627 | 3650 | 1513 | 3950 | 1347 | 4250 | 844 | |||
| 3360 | 1623 | 3660 | 1509 | 3960 | 1341 | 4260 | 820 | |||
| 3370 | 1619 | 3670 | 1505 | 3970 | 1336 | 4270 | 796 | |||
| 3380 | 1616 | 3680 | 1499 | 3980 | 1330 | 4280 | 771 | |||
| 3390 | 1612 | 3690 | 1493 | 3990 | 1325 | 4290 | 747 | |||
| 3400 | 1608 | 3700 | 1488 | 4000 | 1319 | 4300 | 723 | |||
| 3410 | 1604 | 3710 | 1482 | 4010 | 1313 | 4310 | 699 | |||
| 3420 | 1600 | 3720 | 1476 | 4020 | 1308 | 4320 | 675 | |||
| 3430 | 1597 | 3730 | 1471 | 4030 | 1302 | |||||
| 3440 | 1593 | 3740 | 1465 | 4040 | 1296 | |||||
| 3450 | 1589 | 3750 | 1460 | 4050 | 1291 | |||||
| 3460 | 1585 | 3760 | 1454 | 4060 | 1285 | |||||
| 3470 | 1581 | 3770 | 1448 | 4070 | 1280 | |||||
| 3480 | 1577 | 3780 | 1443 | 4080 | 1255 | |||||
| 3490 | 1574 | 3790 | 1437 | 4090 | 1231 | |||||
| 3500 | 1570 | 3800 | 1431 | 4100 | 1207 | |||||
| 3510 | 1566 | 3810 | 1426 | 4110 | 1183 | |||||
| 3520 | 1562 | 3820 | 1420 | 4120 | 1159 | |||||
| 3530 | 1558 | 3830 | 1415 | 4130 | 1134 | |||||
| 3540 | 1555 | 3840 | 1409 | 4140 | 1110 | |||||
| 3550 | 1551 | 3850 | 1403 | 4150 | 1086 | |||||
| 3560 | 1547 | 3860 | 1398 | 4160 | 1062 | |||||
| 3570 | 1543 | 3870 | 1392 | 4170 | 1038 | |||||
| 3580 | 1539 | 3880 | 1386 | 4180 | 1013 | |||||
| 3590 | 1535 | 3890 | 1381 | 4190 | 989 | |||||
| 3600 | 1532 | 3900 | 1375 | 4200 | 965 |
A.8.4 GÁLIBO GEC16
| Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 430 | 1650 | ||||||||||||
| 3290 | 1650 | ||||||||||||
| 3300 | 1648 | 3600 | 1605 | 3900 | 1562 | 4200 | 1519 | 4500 | 1476 | ||||
| 3310 | 1647 | 3610 | 1604 | 3910 | 1561 | 4210 | 1518 | 4510 | 1475 | ||||
| 3320 | 1645 | 3620 | 1602 | 3920 | 1559 | 4220 | 1516 | 4520 | 1473 | ||||
| 3330 | 1644 | 3630 | 1601 | 3930 | 1558 | 4230 | 1515 | 4530 | 1472 | ||||
| 3340 | 1642 | 3640 | 1599 | 3940 | 1556 | 4240 | 1513 | 4540 | 1470 | ||||
| 3350 | 1641 | 3650 | 1598 | 3950 | 1555 | 4250 | 1512 | 4550 | 1469 | ||||
| 3360 | 1639 | 3660 | 1596 | 3960 | 1553 | 4260 | 1510 | 4560 | 1467 | ||||
| 3370 | 1638 | 3670 | 1595 | 3970 | 1552 | 4270 | 1509 | 4570 | 1466 | ||||
| 3380 | 1637 | 3680 | 1594 | 3980 | 1551 | 4280 | 1508 | 4580 | 1465 | ||||
| 3390 | 1635 | 3690 | 1592 | 3990 | 1549 | 4290 | 1506 | 4590 | 1463 | ||||
| 3400 | 1634 | 3700 | 1591 | 4000 | 1548 | 4300 | 1505 | 4600 | 1462 | ||||
| 3410 | 1632 | 3710 | 1589 | 4010 | 1546 | 4310 | 1503 | 4610 | 1460 | ||||
| 3420 | 1631 | 3720 | 1588 | 4020 | 1545 | 4320 | 1502 | 4620 | 1459 | ||||
| 3430 | 1629 | 3730 | 1586 | 4030 | 1543 | 4330 | 1500 | 4630 | 1457 | ||||
| 3440 | 1628 | 3740 | 1585 | 4040 | 1542 | 4340 | 1499 | 4640 | 1456 | ||||
| 3450 | 1627 | 3750 | 1584 | 4050 | 1541 | 4350 | 1498 | 4650 | 1455 | ||||
| 3460 | 1625 | 3760 | 1582 | 4060 | 1539 | 4360 | 1496 | ||||||
| 3470 | 1624 | 3770 | 1581 | 4070 | 1538 | 4370 | 1495 | ||||||
| 3480 | 1622 | 3780 | 1579 | 4080 | 1536 | 4380 | 1493 | ||||||
| 3490 | 1621 | 3790 | 1578 | 4090 | 1535 | 4390 | 1492 | ||||||
| 3500 | 1619 | 3800 | 1576 | 4100 | 1533 | 4400 | 1490 | ||||||
| 3510 | 1618 | 3810 | 1575 | 4110 | 1532 | 4410 | 1489 | ||||||
| 3520 | 1617 | 3820 | 1574 | 4120 | 1530 | 4420 | 1487 | ||||||
| 3530 | 1615 | 3830 | 1572 | 4130 | 1529 | 4430 | 1486 | ||||||
| 3540 | 1614 | 3840 | 1571 | 4140 | 1528 | 4440 | 1485 | ||||||
| 3550 | 1612 | 3850 | 1569 | 4150 | 1526 | 4450 | 1483 | ||||||
| 3560 | 1611 | 3860 | 1568 | 4160 | 1525 | 4460 | 1482 | ||||||
| 3570 | 1609 | 3870 | 1566 | 4170 | 1523 | 4470 | 1480 | ||||||
| 3580 | 1608 | 3880 | 1565 | 4180 | 1522 | 4480 | 1479 | ||||||
| 3590 | 1606 | 3890 | 1563 | 4190 | 1520 | 4490 | 1477 | ||||||
| 3600 | 1605 | 3900 | 1562 | 4200 | 1519 | 4500 | 1476 |
A.8.5 GÁLIBO GA
| Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 430 | 1575 | |||||||||
| 3200 | 1575 | 3500 | 1443 | 3800 | 1303 | 4100 | 908 | |||
| 3210 | 1575 | 3510 | 1439 | 3810 | 1298 | 4110 | 887 | |||
| 3220 | 1575 | 3520 | 1434 | 3820 | 1294 | 4120 | 867 | |||
| 3230 | 1570 | 3530 | 1429 | 3830 | 1289 | 4130 | 847 | |||
| 3240 | 1565 | 3540 | 1425 | 3840 | 1284 | 4140 | 826 | |||
| 3250 | 1560 | 3550 | 1420 | 3850 | 1280 | 4150 | 806 | |||
| 3260 | 1556 | 3560 | 1415 | 3860 | 1266 | 4160 | 785 | |||
| 3270 | 1551 | 3570 | 1411 | 3870 | 1253 | 4170 | 765 | |||
| 3280 | 1546 | 3580 | 1406 | 3880 | 1239 | 4180 | 745 | |||
| 3290 | 1542 | 3590 | 1401 | 3890 | 1226 | 4190 | 724 | |||
| 3300 | 1537 | 3600 | 1397 | 3900 | 1212 | 4200 | 704 | |||
| 3310 | 1532 | 3610 | 1392 | 3910 | 1199 | 4210 | 684 | |||
| 3320 | 1528 | 3620 | 1387 | 3920 | 1185 | 4220 | 663 | |||
| 3330 | 1523 | 3630 | 1383 | 3930 | 1172 | 4230 | 643 | |||
| 3340 | 1518 | 3640 | 1378 | 3940 | 1158 | 4240 | 622 | |||
| 3350 | 1514 | 3650 | 1373 | 3950 | 1145 | 4250 | 602 | |||
| 3360 | 1509 | 3660 | 1368 | 3960 | 1131 | 4260 | 582 | |||
| 3370 | 1504 | 3670 | 1364 | 3970 | 1118 | 4270 | 561 | |||
| 3380 | 1500 | 3680 | 1359 | 3980 | 1104 | 4280 | 541 | |||
| 3390 | 1495 | 3690 | 1354 | 3990 | 1091 | 4290 | 521 | |||
| 3400 | 1490 | 3700 | 1350 | 4000 | 1077 | 4300 | 500 | |||
| 3410 | 1486 | 3710 | 1345 | 4010 | 1064 | 4310 | 480 | |||
| 3420 | 1481 | 3720 | 1340 | 4020 | 1050 | 4320 | 460 | |||
| 3430 | 1476 | 3730 | 1336 | 4030 | 1037 | |||||
| 3440 | 1471 | 3740 | 1331 | 4040 | 1023 | |||||
| 3450 | 1467 | 3750 | 1326 | 4050 | 1010 | |||||
| 3460 | 1462 | 3760 | 1322 | 4060 | 989 | |||||
| 3470 | 1457 | 3770 | 1317 | 4070 | 969 | |||||
| 3480 | 1453 | 3780 | 1312 | 4080 | 948 | |||||
| 3490 | 1448 | 3790 | 1308 | 4090 | 928 | |||||
| 3500 | 1443 | 3800 | 1303 | 4100 | 908 |
A.8.6 GÁLIBO GB
| Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 430 | 1575 | |||||||||
| 3200 | 1575 | 3500 | 1478 | 3800 | 1376 | 4100 | 1211 | |||
| 3210 | 1575 | 3510 | 1475 | 3810 | 1372 | 4110 | 1177 | |||
| 3220 | 1575 | 3520 | 1472 | 3820 | 1369 | 4120 | 1143 | |||
| 3230 | 1571 | 3530 | 1468 | 3830 | 1365 | 4130 | 1109 | |||
| 3240 | 1568 | 3540 | 1465 | 3840 | 1362 | 4140 | 1074 | |||
| 3250 | 1564 | 3550 | 1461 | 3850 | 1358 | 4150 | 1040 | |||
| 3260 | 1561 | 3560 | 1458 | 3860 | 1355 | 4160 | 1006 | |||
| 3270 | 1557 | 3570 | 1454 | 3870 | 1352 | 4170 | 972 | |||
| 3280 | 1554 | 3580 | 1451 | 3880 | 1348 | 4180 | 938 | |||
| 3290 | 1550 | 3590 | 1448 | 3890 | 1345 | 4190 | 904 | |||
| 3300 | 1547 | 3600 | 1444 | 3900 | 1341 | 4200 | 869 | |||
| 3310 | 1544 | 3610 | 1441 | 3910 | 1338 | 4210 | 835 | |||
| 3320 | 1540 | 3620 | 1437 | 3920 | 1334 | 4220 | 801 | |||
| 3330 | 1537 | 3630 | 1434 | 3930 | 1331 | 4230 | 767 | |||
| 3340 | 1533 | 3640 | 1430 | 3940 | 1328 | 4240 | 733 | |||
| 3350 | 1530 | 3650 | 1427 | 3950 | 1324 | 4250 | 699 | |||
| 3360 | 1526 | 3660 | 1424 | 3960 | 1321 | 4260 | 664 | |||
| 3370 | 1523 | 3670 | 1420 | 3970 | 1317 | 4270 | 630 | |||
| 3380 | 1520 | 3680 | 1417 | 3980 | 1314 | 4280 | 596 | |||
| 3390 | 1516 | 3690 | 1413 | 3990 | 1310 | 4290 | 562 | |||
| 3400 | 1513 | 3700 | 1410 | 4000 | 1307 | 4300 | 528 | |||
| 3410 | 1509 | 3710 | 1406 | 4010 | 1304 | 4310 | 494 | |||
| 3420 | 1506 | 3720 | 1403 | 4020 | 1300 | 4320 | 460 | |||
| 3430 | 1502 | 3730 | 1400 | 4030 | 1297 | |||||
| 3440 | 1499 | 3740 | 1396 | 4040 | 1293 | |||||
| 3450 | 1496 | 3750 | 1393 | 4050 | 1290 | |||||
| 3460 | 1492 | 3760 | 1389 | 4060 | 1286 | |||||
| 3470 | 1489 | 3770 | 1386 | 4070 | 1283 | |||||
| 3480 | 1485 | 3780 | 1382 | 4080 | 1280 | |||||
| 3490 | 1482 | 3790 | 1379 | 4090 | 1245 | |||||
| 3500 | 1478 | 3800 | 1376 | 4100 | 1211 |
A.8.7 GÁLIBO GC
| Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 430 | 1575 | |||||||||
| 3500 | 1575 | 3800 | 1543 | 4100 | 1512 | 4400 | 1481 | |||
| 3510 | 1573 | 3810 | 1542 | 4110 | 1511 | 4410 | 1480 | |||
| 3520 | 1572 | 3820 | 1541 | 4120 | 1510 | 4420 | 1479 | |||
| 3530 | 1571 | 3830 | 1540 | 4130 | 1509 | 4430 | 1477 | |||
| 3540 | 1570 | 3840 | 1539 | 4140 | 1508 | 4440 | 1476 | |||
| 3550 | 1569 | 3850 | 1538 | 4150 | 1507 | 4450 | 1475 | |||
| 3560 | 1568 | 3860 | 1537 | 4160 | 1506 | 4460 | 1474 | |||
| 3570 | 1567 | 3870 | 1536 | 4170 | 1505 | 4470 | 1473 | |||
| 3580 | 1566 | 3880 | 1535 | 4180 | 1504 | 4480 | 1472 | |||
| 3590 | 1565 | 3890 | 1534 | 4190 | 1503 | 4490 | 1471 | |||
| 3600 | 1564 | 3900 | 1533 | 4200 | 1501 | 4500 | 1470 | |||
| 3610 | 1563 | 3910 | 1532 | 4210 | 1500 | 4510 | 1469 | |||
| 3620 | 1562 | 3920 | 1531 | 4220 | 1499 | 4520 | 1468 | |||
| 3630 | 1561 | 3930 | 1530 | 4230 | 1498 | 4530 | 1467 | |||
| 3640 | 1560 | 3940 | 1529 | 4240 | 1497 | 4540 | 1466 | |||
| 3650 | 1559 | 3950 | 1528 | 4250 | 1496 | 4550 | 1465 | |||
| 3660 | 1558 | 3960 | 1527 | 4260 | 1495 | 4560 | 1464 | |||
| 3670 | 1557 | 3970 | 1525 | 4270 | 1494 | 4570 | 1463 | |||
| 3680 | 1556 | 3980 | 1524 | 4280 | 1493 | 4580 | 1462 | |||
| 3690 | 1555 | 3990 | 1523 | 4290 | 1492 | 4590 | 1461 | |||
| 3700 | 1554 | 4000 | 1522 | 4300 | 1491 | 4600 | 1460 | |||
| 3710 | 1553 | 4010 | 1521 | 4310 | 1490 | 4610 | 1459 | |||
| 3720 | 1552 | 4020 | 1520 | 4320 | 1489 | 4620 | 1458 | |||
| 3730 | 1551 | 4030 | 1519 | 4330 | 1488 | 4630 | 1457 | |||
| 3740 | 1549 | 4040 | 1518 | 4340 | 1487 | 4640 | 1456 | |||
| 3750 | 1548 | 4050 | 1517 | 4350 | 1486 | 4650 | 1455 | |||
| 3760 | 1547 | 4060 | 1516 | 4360 | 1485 | |||||
| 3770 | 1546 | 4070 | 1515 | 4370 | 1484 | |||||
| 3780 | 1545 | 4080 | 1514 | 4380 | 1483 | |||||
| 3790 | 1544 | 4090 | 1513 | 4390 | 1482 | |||||
| 3800 | 1543 | 4100 | 1512 | 4400 | 1481 |
A.8.8 GÁLIBO GEE10
| Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | ||
|---|---|---|---|---|---|---|---|
| 430 | 1425 | ||||||
| 3500 | 1425 | 3700 | 1242 | 3900 | 966 | ||
| 3510 | 1425 | 3710 | 1232 | 3910 | 932 | ||
| 3520 | 1425 | 3720 | 1222 | 3920 | 897 | ||
| 3530 | 1414 | 3730 | 1212 | 3930 | 863 | ||
| 3540 | 1404 | 3740 | 1201 | 3940 | 828 | ||
| 3550 | 1394 | 3750 | 1191 | 3950 | 794 | ||
| 3560 | 1384 | 3760 | 1181 | 3960 | 759 | ||
| 3570 | 1374 | 3770 | 1171 | 3970 | 725 | ||
| 3580 | 1364 | 3780 | 1161 | 3980 | 690 | ||
| 3590 | 1354 | 3790 | 1151 | 3990 | 656 | ||
| 3600 | 1343 | 3800 | 1141 | 4000 | 621 | ||
| 3610 | 1333 | 3810 | 1130 | 4010 | 587 | ||
| 3620 | 1323 | 3820 | 1120 | 4020 | 552 | ||
| 3630 | 1313 | 3830 | 1110 | 4030 | 518 | ||
| 3640 | 1303 | 3840 | 1100 | 4040 | 483 | ||
| 3650 | 1293 | 3850 | 1090 | 4050 | 449 | ||
| 3660 | 1283 | 3860 | 1080 | 4060 | 414 | ||
| 3670 | 1272 | 3870 | 1070 | 4070 | 380 | ||
| 3680 | 1262 | 3880 | 1035 | ||||
| 3690 | 1252 | 3890 | 1001 | ||||
| 3700 | 1242 | 3900 | 966 |
A.8.9 GÁLIBO GED10
| Altura s/carril (mm) | Semiancho (mm) | Altura s/carril (mm) | Semiancho (mm) | |
|---|---|---|---|---|
| 430 | 1425 | |||
| 3500 | 1425 | 3700 | 1147 | |
| 3510 | 1425 | 3710 | 1132 | |
| 3520 | 1425 | 3720 | 1117 | |
| 3530 | 1409 | 3730 | 1101 | |
| 3540 | 1394 | 3740 | 1086 | |
| 3550 | 1378 | 3750 | 1070 | |
| 3560 | 1363 | 3760 | 1055 | |
| 3570 | 1348 | 3770 | 1040 | |
| 3580 | 1332 | 3780 | 1000 | |
| 3590 | 1317 | 3790 | 960 | |
| 3600 | 1301 | 3800 | 920 | |
| 3610 | 1286 | 3810 | 880 | |
| 3620 | 1271 | 3820 | 840 | |
| 3630 | 1255 | 3830 | 800 | |
| 3640 | 1240 | 3840 | 760 | |
| 3650 | 1224 | 3850 | 720 | |
| 3660 | 1209 | 3860 | 680 | |
| 3670 | 1194 | 3870 | 640 | |
| 3680 | 1178 | |||
| 3690 | 1163 | |||
| 3700 | 1147 |
A.9.1 GÁLIBOS GHE16, GEA16, GEB16, GEC16, GA, GB Y GC
| Empate, a, del vehículo (en m) | Distancia, n, de la sección transversal considerada al eje extremo más próximo (vagón de ejes) o al pivote más cercano (vagón de bogies), expresada en m | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | 5,5 | 6 | 6,5 | 7 | 7,5 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| 7,5 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||||||||||||||
| 8 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |||||||||||||||
| 9 | 0 | 0 | 0 | 1 | 1 | 2 | 2 | 2 | 2 | ||||||||||||||
| 10 | 0 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 3 | |||||||||||||
| 11 | 0 | 0 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 4 | 4 | ||||||||||||
| 12 | 0 | 0 | 1 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 5 | 5 | |||||||||||
| 13 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 5 | 6 | 6 | 6 | 6 | 6 | ||||||||||
| 14 | 0 | 1 | 2 | 3 | 4 | 5 | 5 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | |||||||||
| 15 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | 8 | 8 | 9 | 9 | 9 | 9 | ||||||||
| 16 | 0 | 1 | 2 | 4 | 5 | 6 | 7 | 8 | 8 | 9 | 10 | 10 | 10 | 11 | 11 | 11 | |||||||
| 17 | 0 | 1 | 3 | 4 | 5 | 6 | 7 | 9 | 9 | 10 | 11 | 11 | 12 | 12 | 12 | 12 | 12 | ||||||
| 18 | 0 | 1 | 3 | 4 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 12 | 13 | 13 | 14 | 14 | 14 | ||||||
| 19 | 0 | 2 | 3 | 5 | 6 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 14 | 15 | 15 | 16 | 16 | 16 | |||||
| 19,5 | 0 | 2 | 3 | 5 | 7 | 8 | 9 | 10 | 11 | 13 | 13 | 14 | 15 | 15 | 16 | 16 | 17 | 17 | |||||
| 20 | 0 | 2 | 4 | 5 | 7 | 8 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 16 | 17 | 17 | 18 | 18 | |||||
| 20,5 | 0 | 2 | 4 | 5 | 7 | 8 | 10 | 11 | 12 | 13 | 15 | 15 | 16 | 17 | 17 | 18 | 19 | 20 | 20 | ||||
| 21 | 0 | 2 | 4 | 6 | 7 | 9 | 10 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 19 | 21 | 21 | 21 | ||||
| 21,5 | 0 | 2 | 4 | 6 | 8 | 9 | 11 | 12 | 13 | 15 | 16 | 17 | 17 | 19 | 20 | 21 | 22 | 23 | 23 | ||||
| 22 | 0 | 2 | 4 | 6 | 8 | 9 | 11 | 12 | 14 | 15 | 16 | 17 | 18 | 20 | 21 | 22 | 24 | 25 | 25 | ||||
| 24 | 0 | 3 | 5 | 7 | 9 | 11 | 12 | 14 | 16 | 17 | 19 | 21 | 23 | 24 | 26 | 27 | 30 | 31 | 32 | 33 | |||
| 26 | 1 | 3 | 5 | 8 | 10 | 12 | 14 | 16 | 17 | 20 | 22 | 25 | 27 | 29 | 31 | 33 | 36 | 38 | 40 | 41 | 41 | ||
| 28 | 1 | 3 | 6 | 8 | 11 | 13 | 15 | 17 | 20 | 23 | 26 | 29 | 31 | 34 | 36 | 38 | 42 | 45 | 47 | 49 | 50 | 50 | |
| 30 | 1 | 4 | 7 | 9 | 12 | 14 | 17 | 19 | 23 | 26 | 30 | 33 | 36 | 38 | 41 | 43 | 48 | 51 | 54 | 57 | 58 | 59 | 60 |
|
NOTAS: 1. Para valores de a (distancias entre ejes o pivotes) o de n (distancias entre la sección transversal considerada y el eje o pivote más próximo), no indicados en el cuadro, se tomará el valor inmediato superior. 2. Para valores de a < 7,5 m se considerará una reducción nula. |
|||||||||||||||||||||||
|
Cuadro A.9.1.Reducción (en cm) de la anchura del cargamento en secciones internas (Eist). Gálibos GHE16, GEA16, GEB16, GEC16, GA, GB Y GC |
|||||||||||||||||||||||
Correcciones a aplicar a los valores del cuadro A.9.1:
1. Para alturas h< 0,430 m sobre cota de carril, las reducciones de la anchura del cargamento Eist indicadas en el cuadro se incrementarán en ΔEist = 5 cm.
2. Para alturas h≥ 3,32 m (en GA), h≥ 3,35 m (en GEA16), h≥ 3,36 m (en GB) y h≥ 3,44 m (en GEB16), las reducciones de la anchura del cargamento Eist indicadas en el cuadro se disminuirán en los valores indicados en el cuadro A.9.2.
| Gálibo | Altura h (m) a partir de la que se aplica la minoración de la reducción | |||||
|---|---|---|---|---|---|---|
| GA | 3,32 | 3,42 | 3,51 | 3,61 | 3,71 | 3,81 |
| GEA16 | 3,35 | 3,41 | 3,47 | 3,52 | 3,58 | 3,64 |
| GB | 3,36 | 3,49 | 3,62 | 3,75 | 3,89 | 4,02 |
| GEB16 | 3,44 | 3,56 | 3,68 | 3,81 | 3,93 | 4,05 |
| Valor (cm) a restar a la reducción obtenida del cuadro A.9.1. | 1 | 2 | 3 | 4 | 5 | 6 |
|
Cuadro A.9.2. Minoración de la reducción en los gálibos GEA16, GEB16, GA y GB |
||||||
3. En cargamentos susceptibles de basculación durante la marcha del vagón, las reducciones de la anchura del cargamento Eist indicadas en el cuadro se incrementarán:
– ΔEist =10 cm, para cargamentos de mercancías apiladas que sobrepasen los teleros (por ej. mallazo).
– ΔEist =5 cm, para cargamentos de vehículos sobre neumáticos sujetos solo con calces, en las comprobación de alturas h> 3,20 m. sobre cota de carril. Se excluyen los vehículos cargados en el piso superior de vagones de dos pisos.
4. En vagones con bogies, las reducciones de la anchura del cargamento Eist indicadas en el cuadro se incrementarán en función del empate (p) del bogie:
– Para:  . ΔEist =1 cm.
. ΔEist =1 cm.
– Para:  . ΔEist =2 cm.
. ΔEist =2 cm.
5. En cargamentos sobre vagones provistos de traviesa giratoria o sobre vagones de seguridad o intermedios (utilizados para cargamentos que excedan la longitud útil del vagón), se aplicará el cuadro del Anejo 12.
A.9.2 GÁLIBOS GEE10 Y GED10
| Empate, a, del vehículo (en m) | Distancia, n, de la sección transversal considerada al eje extremo más próximo (vagón de ejes) o al pivote más cercano (vagón de bogies), expresada en m | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | 5,5 | 6 | |
| 6 | 0 | 0 | 1 | 2 | 2 | 2 | ||||||
| 6,5 | 0 | 0 | 1 | 2 | 3 | 3 | 3 | |||||
| 7 | 0 | 1 | 2 | 3 | 3 | 4 | 4 | |||||
| 7,5 | 0 | 1 | 2 | 3 | 4 | 4 | 5 | 5 | ||||
| 8 | 0 | 1 | 2 | 4 | 4 | 5 | 5 | 6 | ||||
| 9 | 0 | 2 | 3 | 5 | 6 | 7 | 7 | 8 | 8 | |||
| 10 | 0 | 2 | 4 | 6 | 7 | 8 | 9 | 10 | 10 | 10 | ||
| 11 | 0 | 3 | 5 | 7 | 8 | 10 | 11 | 12 | 12 | 13 | 13 | |
| 12 | 0 | 3 | 5 | 8 | 9 | 11 | 12 | 14 | 14 | 15 | 15 | 16 |
| 13 | 1 | 4 | 6 | 9 | 11 | 13 | 14 | 16 | 17 | 18 | 18 | 19 |
| 14 | 1 | 4 | 7 | 10 | 12 | 14 | 16 | 18 | 19 | 21 | 22 | 23 |
| 15 | 1 | 5 | 8 | 11 | 13 | 16 | 18 | 20 | 22 | 24 | 25 | 26 |
|
1. Para valores de a (distancias entre ejes o pivotes) o de n (distancias entre la sección transversal considerada y el eje o pivote más próximo), no indicados en el cuadro, se tomará el valor inmediato superior. 2. Para valores de a < 6 m se considerará una reducción nula. |
||||||||||||
|
Cuadro A.9.3. Reducción (en cm) de la anchura del cargamento en secciones internas (Eist). Gálibos GEE10 y GED10 |
||||||||||||
A.10.1 GÁLIBOS GHE16, GEA16, GEB16, GEC16, GA, GB Y GC
| Empate, a, del vehículo (en m) | Distancia, n, de la sección transversal considerada al eje extremo más próximo (vagón de ejes) o al pivote más cercano (vagón de bogies), expresada en m | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0,5 | 1 | 1,5 | 1,75 | 2 | 2,25 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | 5,5 | 6 | 6,5 | 7 | 7,5 | 8 | 8,5 | 9 | 9,5 | 10 | |
| 7,5 | 0 | 1 | 3 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | 15 | 17 | 20 | 22 | 25 | 28 | 30 | 34 | 38 | 43 | 48 | 54 |
| 8 | 0 | 1 | 3 | 3 | 4 | 5 | 6 | 8 | 10 | 12 | 15 | 17 | 20 | 22 | 25 | 28 | 31 | 35 | 39 | 44 | 49 | 54 |
| 9 | 0 | 1 | 3 | 3 | 4 | 5 | 6 | 8 | 10 | 13 | 15 | 17 | 20 | 23 | 25 | 28 | 31 | 36 | 40 | 46 | 50 | 56 |
| 10 | 0 | 1 | 3 | 3 | 5 | 5 | 7 | 9 | 11 | 13 | 15 | 18 | 20 | 23 | 26 | 29 | 33 | 38 | 42 | 48 | 53 | 59 |
| 11 | 0 | 1 | 3 | 4 | 5 | 6 | 7 | 9 | 11 | 13 | 16 | 18 | 21 | 24 | 27 | 30 | 35 | 40 | 44 | 50 | 55 | 61 |
| 12 | 0 | 1 | 3 | 4 | 5 | 6 | 7 | 9 | 12 | 14 | 16 | 19 | 22 | 24 | 27 | 32 | 37 | 42 | 47 | 52 | 57 | 64 |
| 13 | 0 | 1 | 3 | 4 | 5 | 6 | 7 | 10 | 12 | 15 | 17 | 20 | 22 | 25 | 29 | 34 | 39 | 44 | 49 | 55 | 60 | 66 |
| 14 | 0 | 2 | 4 | 4 | 6 | 7 | 8 | 10 | 13 | 15 | 18 | 20 | 23 | 26 | 31 | 36 | 41 | 46 | 51 | 57 | 63 | 69 |
| 15 | 0 | 2 | 4 | 5 | 6 | 7 | 8 | 11 | 13 | 16 | 18 | 21 | 24 | 28 | 33 | 38 | 43 | 49 | 54 | 60 | 65 | 72 |
| 16 | 0 | 2 | 4 | 5 | 6 | 7 | 9 | 11 | 14 | 16 | 19 | 22 | 25 | 30 | 35 | 40 | 45 | 51 | 56 | 62 | 68 | 75 |
| 17 | 0 | 2 | 4 | 5 | 7 | 8 | 9 | 12 | 14 | 17 | 20 | 23 | 26 | 31 | 37 | 42 | 48 | 53 | 59 | 65 | 71 | 78 |
| 18 | 0 | 2 | 4 | 6 | 7 | 8 | 9 | 12 | 15 | 18 | 21 | 24 | 28 | 33 | 39 | 44 | 50 | 56 | 61 | 68 | 74 | 81 |
| 19 | 0 | 2 | 5 | 6 | 7 | 8 | 10 | 13 | 15 | 18 | 21 | 24 | 30 | 35 | 41 | 46 | 52 | 58 | 64 | 71 | 77 | 84 |
| 19,5 | 0 | 2 | 5 | 6 | 7 | 9 | 10 | 13 | 16 | 19 | 22 | 25 | 30 | 36 | 41 | 47 | 53 | 59 | 65 | 72 | 78 | 85 |
| 20 | 0 | 3 | 5 | 6 | 8 | 9 | 10 | 13 | 16 | 19 | 22 | 26 | 31 | 37 | 42 | 48 | 54 | 61 | 67 | 73 | 80 | 87 |
| 20,5 | 0 | 3 | 5 | 6 | 8 | 9 | 11 | 13 | 16 | 19 | 23 | 27 | 32 | 38 | 44 | 49 | 55 | 62 | 68 | 75 | 81 | 88 |
| 21 | 0 | 3 | 5 | 6 | 8 | 9 | 11 | 14 | 17 | 20 | 23 | 28 | 33 | 39 | 45 | 51 | 57 | 63 | 69 | 76 | 83 | 90 |
| 21,5 | 0 | 3 | 5 | 7 | 8 | 9 | 11 | 14 | 17 | 20 | 23 | 28 | 34 | 40 | 46 | 52 | 58 | 64 | 71 | 78 | 84 | 91 |
| 22 | 0 | 3 | 6 | 7 | 8 | 10 | 11 | 14 | 17 | 20 | 24 | 29 | 35 | 41 | 47 | 53 | 59 | 65 | 72 | 79 | 86 | 93 |
| 24 | 0 | 3 | 6 | 7 | 9 | 10 | 12 | 15 | 19 | 22 | 26 | 32 | 38 | 44 | 51 | 57 | 64 | 71 | 77 | 85 | 92 | 99 |
| 26 | 1 | 4 | 7 | 8 | 10 | 11 | 13 | 16 | 20 | 23 | 29 | 35 | 42 | 48 | 55 | 62 | 68 | 76 | 83 | 90 | 98 | 106 |
| 28 | 1 | 4 | 7 | 9 | 11 | 12 | 14 | 17 | 21 | 26 | 32 | 39 | 45 | 52 | 59 | 66 | 73 | 81 | 88 | 96 | 104 | 112 |
| 30 | 1 | 4 | 8 | 9 | 11 | 13 | 15 | 19 | 22 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 78 | 86 | 94 | 102 | 110 | 119 |
|
NOTA: 1. Para valores de a (distancias entre ejes o pivotes) o de n (distancias entre la sección transversal considerada y el eje o pivote más próximo), no indicados en el cuadro, se tomará el valor inmediato superior. |
||||||||||||||||||||||
|
Cuadro A.10.1. Reducción (en cm) de la anchura del cargamento en secciones externas (East). Gálibos GHE16, GEA16, GEB16, GEC16, GA, GB y GC |
||||||||||||||||||||||
Correcciones a aplicar a los valores del cuadro A.10.1:
Las mismas que las indicadas en los puntos 1, 2, 3 y 5 para el cuadro A.9.1 del anejo 9.
A.10.2 GÁLIBOS GEE10 Y GED10
| Empate, a, del vehículo (en m) | Distancia, n, de la sección transversal considerada al eje extremo más próximo (vagón de ejes) o al pivote más cercano (vagón de bogies), expresada en m | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0,5 | 1 | 1,5 | 1,75 | 2 | 2,25 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | 5,5 | 6 | |
| 6 | 0 | 2 | 5 | 6 | 8 | 9 | 11 | 15 | 19 | 23 | 27 | 33 | 39 | 45 |
| 6,5 | 0 | 2 | 5 | 6 | 8 | 10 | 12 | 15 | 19 | 23 | 28 | 34 | 40 | 46 |
| 7 | 0 | 2 | 5 | 7 | 9 | 10 | 12 | 16 | 20 | 24 | 29 | 35 | 41 | 47 |
| 7,5 | 0 | 2 | 5 | 7 | 9 | 10 | 12 | 16 | 20 | 25 | 30 | 36 | 42 | 49 |
| 8 | 0 | 3 | 6 | 7 | 9 | 11 | 13 | 17 | 21 | 25 | 31 | 37 | 43 | 50 |
| 9 | 0 | 3 | 6 | 8 | 10 | 12 | 14 | 18 | 22 | 27 | 33 | 40 | 46 | 53 |
| 10 | 0 | 3 | 7 | 9 | 11 | 13 | 15 | 19 | 24 | 29 | 36 | 42 | 49 | 56 |
| 11 | 0 | 4 | 8 | 9 | 12 | 13 | 16 | 20 | 25 | 32 | 38 | 45 | 52 | 60 |
| 12 | 0 | 4 | 8 | 10 | 12 | 14 | 17 | 22 | 27 | 34 | 41 | 48 | 55 | 63 |
| 13 | 1 | 5 | 9 | 11 | 13 | 15 | 18 | 23 | 29 | 36 | 43 | 51 | 58 | 66 |
| 14 | 1 | 5 | 10 | 12 | 14 | 16 | 19 | 25 | 31 | 38 | 46 | 53 | 61 | 70 |
| 15 | 1 | 6 | 10 | 12 | 15 | 18 | 20 | 26 | 33 | 41 | 48 | 56 | 65 | 73 |
|
NOTAS: 1. Para valores de a (distancias entre ejes o pivotes) o de n (distancias entre la sección transversal considerada y el eje o pivote más próximo), no indicados en el cuadro, se tomará el valor inmediato superior. |
||||||||||||||
|
Cuadro A.10.2. Reducción (en cm) de la anchura del cargamento en secciones externas (East). Gálibos GEE10 y GED10 |
||||||||||||||
A.10.3 EJEMPLO DE CÁLCULO DE LA REDUCCIÓN DE LA ANCHURA DEL CARGAMENTO MEDIANTE CUADROS
Se considera un gálibo GHE16.
| Datos del vagón | Dos ejes, a= 7,2 m |
| Datos del cargamento (figura A.10.1) |
∙ Longitud: 11,2 m ∙ Distancia entre extremos y ejes del vagón: 2,1 y 1,9 m. ∙ Separación lateral mínima entre el cargamento y el contorno de referencia, en el punto más desfavorable (zona del techo): 6 cm. |
Al tratarse de un vagón, son aplicables los cuadros de los anejos 9 y 10, para el cálculo de las reducciones mínimas del cargamento respecto al contorno de referencia. No es de aplicación ninguna de las correcciones indicadas en los anejos 9 y 10.
Para secciones internas, entrando en el cuadro A.9.1 del Anejo 9, con los valores:
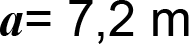 (se toma el valor inmediato superior:
(se toma el valor inmediato superior:  )
)
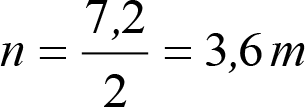 (se toma el valor inmediato superior:
(se toma el valor inmediato superior:  )
)
se obtiene una reducción Eist=1 < 6 cm (distancia mínima entre el cargamento analizado y el contorno del gálibo), por lo que se cumple el gálibo de cargamento en secciones internas.
Para secciones externas, entrando en el cuadro A.10.1 del Anejo 10, con los valores:
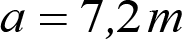 (se toma el valor inmediato superior:
(se toma el valor inmediato superior:  )
)
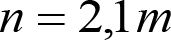 (se toma el valor inmediato superior:
(se toma el valor inmediato superior: 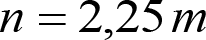 )
)
se obtiene una reducción East=5 cm < 6 cm, por lo que cumple el gálibo de cargamento en secciones externas.
|
Figura A.10.1. Características geométricas del cargamento |
A.11.1 GÁLIBO GEB16
Características del vagón:
| a = 12m | p = 2m | ni = 6m | na = 3m |
| Altura de comprobación del gálibo: h = 4m | |||
Se suponen unas holguras totales constantes de valor: 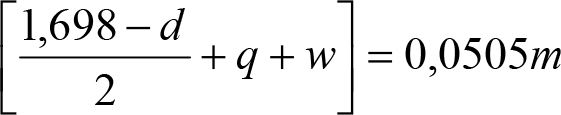
Se aplican las fórmulas del apartado 4.4.3.2.
a) Reducción en secciones internas:
Del cuadro 4.2 (apartado 4.4.2.2), para h=4m: 
Como: 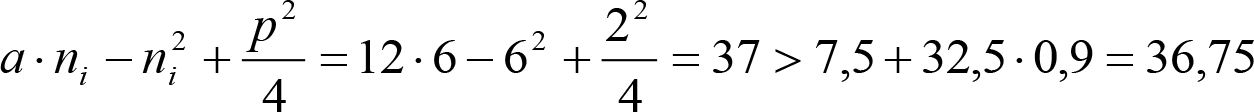 → La máxima reducción se da en curva
→ La máxima reducción se da en curva
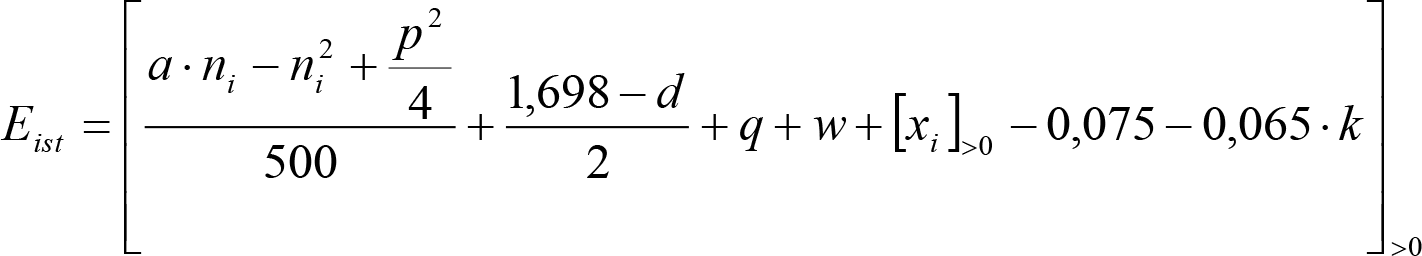
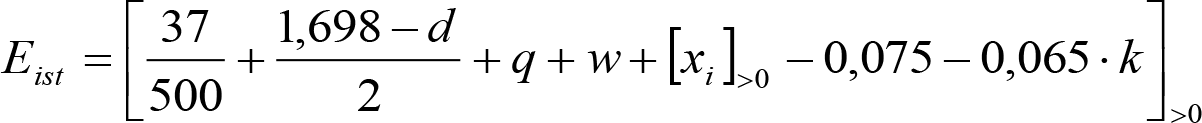

 , por lo que se toma:
, por lo que se toma:  .
.
Alternativamente, a través del cuadro A.9.1 (entrando con a=12 y ni=6) se obtiene una reducción inicial de 5 cm, que tras aplicarle la minoración de 5 cm indicada en el cuadro A.9.2 para h=4m>3,93m, se obtiene una reducción final  , coincidente con la anterior.
, coincidente con la anterior.
b) Reducción en secciones externas:
Como:  → La máxima reducción se da en curva.
→ La máxima reducción se da en curva.

siendo: 
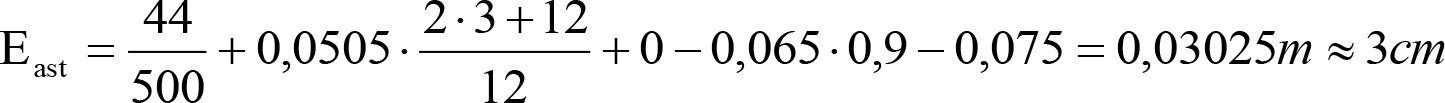
Alternativamente, a través del cuadro A.10.1 (entrando con a=12 y na=3) se obtiene una reducción inicial de 9 cm que tras aplicarle la minoración de 5 cm indicada en el cuadro A.9.2 para h=4m>3,93m se obtiene una reducción final  , la diferencia se debe a que en los cuadros se ha considerado un valor de p = 0 y al redondeo que supone la minoración de 5cm del cuadro A.9.2 para h=4m.
, la diferencia se debe a que en los cuadros se ha considerado un valor de p = 0 y al redondeo que supone la minoración de 5cm del cuadro A.9.2 para h=4m.
A.11.2 GÁLIBO GEC16
Características del vagón:
| a = 12m | p = 0m | ni = 6m | na = 3m |
Se suponen unas holguras totales constantes de valor: 
Se aplican las fórmulas del apartado 4.4.3.1.
a) Reducción en secciones internas:
Como:  → La máxima reducción se da en curva.
→ La máxima reducción se da en curva.
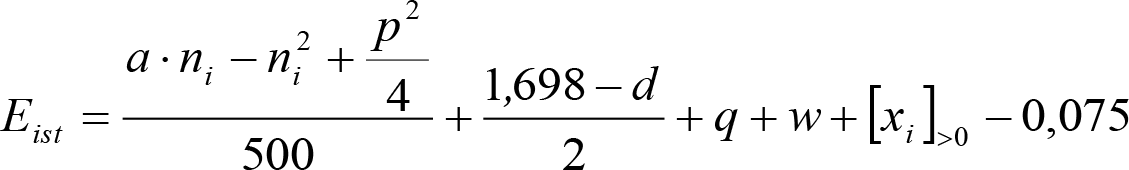
siendo: 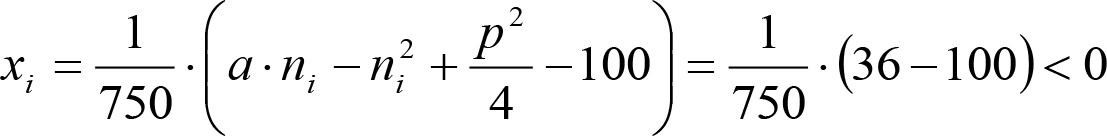
Luego: 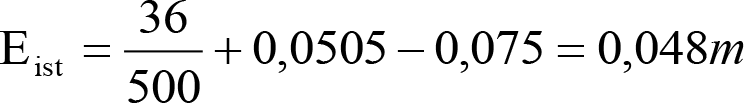
Alternativamente, a través del cuadro A.9.1 se obtiene (entrando con a=12 y ni=6) una reducción de 5 cm, es decir: 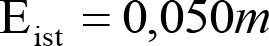 , la diferencia se debe a que en los cuadros se ha considerado un valor de p = 2m.
, la diferencia se debe a que en los cuadros se ha considerado un valor de p = 2m.
b) Reducción en secciones externas:
Como: 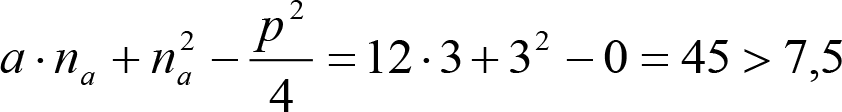 → La máxima reducción se da en curva.
→ La máxima reducción se da en curva.
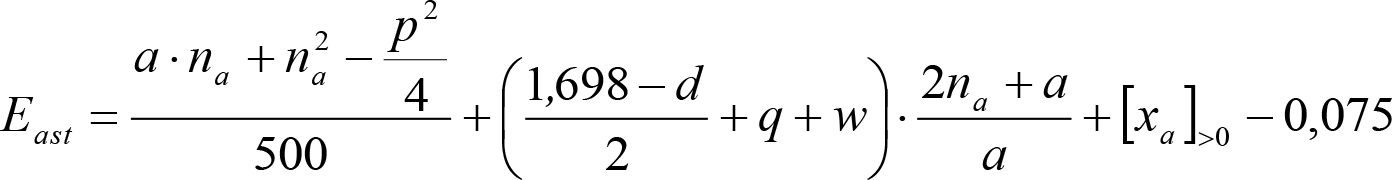
siendo: 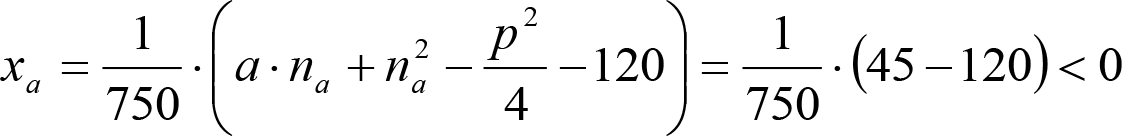
Luego: 
Alternativamente, a través del cuadro A.10.1 se obtiene (entrando con a=12 y na=3) una reducción de 9 cm, es decir: 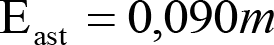 , similar al obtenido por las fórmulas.
, similar al obtenido por las fórmulas.
A.12.1 GÁLIBOS GHE16, GEA16, GEB16, GEC16, GA, GB Y GC (13)
(13) Tabla 2.5 del tomo 1 del anejo 2 del RIV (Reglamento internacional de vehículos). Directivas de cargamento.
La separación horizontal mínima a respetar, a cada lado del vehículo, entre el cargamento y las paredes laterales o los teleros de los vagones de seguridad e intermedios (utilizados para cargamentos que excedan la longitud útil del vagón) se define en el cuadro A.12.1.
| Empate, a, del vehículo (en m) | Vagones de seguridad | Vagones intermedios | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Distancia, n, de la sección transversal considerada al eje extremo más próximo o al pivote más cercano del vagón portador, expresada en m | ||||||||||
| 3 | 4 | 5 | 6 | 6,5 | 7 | 8 | 9 | 10 | ||
| 4 | 26 | |||||||||
| 6 | 26 | 31 | 38 | 45 | 49 | 53 | 61 | 70 | 80 | |
| 8 | 26 | 32 | 39 | 47 | 50 | 55 | 63 | 72 | 83 | |
| 10 | 28 | 34 | 41 | 49 | 54 | 58 | 67 | 77 | 88 | 24 |
| 12 | 29 | 36 | 44 | 52 | 57 | 61 | 71 | 81 | 93 | 28 |
| 14 | 31 | 38 | 47 | 56 | 60 | 65 | 76 | 86 | 98 | 33 |
| 16 | 33 | 41 | 50 | 59 | 64 | 69 | 80 | 92 | 104 | 38 |
| 18 | 34 | 43 | 53 | 63 | 68 | 73 | 85 | 97 | 110 | 44 |
| 20 | 36 | 46 | 56 | 67 | 72 | 78 | 90 | 102 | 116 | 51 |
| 25 | 41 | 52 | 64 | 76 | 83 | 89 | 103 | 117 | 132 | 71 |
| 30 | 46 | 58 | 72 | 86 | 93 | 100 | 116 | 131 | 148 | 95 |
|
NOTAS: 1. Las reducciones en negrita (zona derecha del cuadro) corresponden a cargamentos considerados como transportes excepcionales. 2. Para valores de a (distancias entre ejes o pivotes) o de n (distancias entre la sección transversal considerada y el eje o pivote más próximo del vagón portador), no indicados en el cuadro, se tomará el valor inmediato superior. |
||||||||||
|
Cuadro A.12.1. Separación mínima (en cm) entre el cargamento y las paredes laterales o teleros, en los vagones de seguridad e intermedios. Gálibos GHE16, GEA16, GEB16, GEC16, GA, GB y GC |
||||||||||
Este documento es de carácter informativo y no tiene valor jurídico.
Ayúdenos a mejorar: puede dirigir sus comentarios y sugerencias a nuestro Servicio de atención al ciudadano
Agencia Estatal Boletín Oficial del Estado
Avda. de Manoteras, 54 - 28050 Madrid